Home Resource Centre 12 Key Differences Between Binary Tree And Binary Search Tree

Table of content:

Binary Tree Vs. Binary Search Tree: An Overview
Differences Between Binary Tree And Binary Search Tree (Comparison Table)
What Is A Binary Tree?
What Is A Binary Search Tree?
Key Difference Between Binary Tree And Binary Search Tree Explained
Binary Tree Vs. Binary Search Tree | When To Use Which?
Binary Tree Vs. Binary Search Tree Practical Applications | A Comparative Look
Conclusion
Frequently Asked Questions

12 Key Differences Between Binary Tree And Binary Search Tree

Explore the essential difference between binary tree and binary search tree, examining their structure, performance, and practical applications to help you choose the right data structure.

0 min read

12 Key Differences Between Binary Tree And Binary Search Tree

In today’s world of computer science and software development, data structures form the backbone of efficient algorithms and robust systems. Whether you're a student, a seasoned developer, or simply curious about how data is organized, understanding the subtle yet significant differences between various tree structures is essential. In this article, we will explore the difference between binary tree and binary search tree, two fundamental structures.

Binary Tree Vs. Binary Search Tree: An Overview

Binary Tree: A binary tree is a general-purpose data structure where each node can have up to two children without any inherent ordering.

This flexibility makes binary trees suitable for a variety of applications where data doesn’t require sorting, such as representing hierarchical relationships (e.g., organizational charts or family trees).

Binary Search Tree (BST): A binary search tree is a specialized form of a binary tree that maintains an ordered structure.

In a BST, every node follows a strict ordering rule: all nodes in the left subtree hold values less than the parent node, while all nodes in the right subtree hold values greater than the parent.
This ordering facilitates efficient searching, insertion, and deletion operations, making BSTs ideal for tasks that require fast lookup and dynamic data management.

Differences Between Binary Tree And Binary Search Tree (Comparison Table)

It is important for you to understand the differences between a binary tree and a binary search tree if you want to select the appropriate structure for your specific needs. The table below provides an overview of the differences between them:

Aspect	Binary Tree	Binary Search Tree (BST)
Definition	A hierarchical structure where each node can have at most two children, with no inherent ordering.	A specialized form of binary tree that maintains a specific order: every left descendant is less than the parent, and every right descendant is greater.
Structure & Organization	Lacks an enforced organizational rule beyond the two-child maximum. Nodes can be inserted arbitrarily, resulting in a flexible, non-ordered hierarchy.	Enforces a strict ordering rule, which inherently organizes the tree into a sorted hierarchy. This structured layout directly influences its performance characteristics.
Ordering Principle	No order is maintained among nodes. The placement is arbitrary, and traversals do not yield a sorted sequence.	Enforces a natural order. In-order traversal of a BST produces a sorted sequence, which is fundamental to its design and use in search operations.
Search Performance	Since nodes are not ordered, searching may require examining each node, leading to an average and worst-case time complexity of O(n).	Leverages the ordered structure to enable faster average-case search times of O(log n) when the tree is balanced; however, unbalanced BSTs can degrade to O(n) in the worst-case.
Insertion & Deletion	Insertions and deletions are straightforward, as there is no need to preserve order. Operations depend solely on available positions in the tree.	Insertions and deletions must maintain the ordering property. This often involves additional steps (or even tree re-balancing in self-balancing variants) to preserve optimal performance.
Speed & Efficiency	The lack of order may slow down search-related operations because there’s no guide to direct the search process.	Generally faster for search, insert, and delete operations due to its ordered nature; however, efficiency is contingent on maintaining a balanced structure.
Hierarchy & Traversal	Hierarchical structure is less defined. Traversal orders (pre-, in-, post-order) yield sequences based on arbitrary placement rather than sorted order.	Hierarchical layout is strictly defined by the order; for example, an in-order traversal will always yield a sorted list of elements, providing additional utility for data retrieval.
Variants & Self-Balancing	Includes forms like full, complete, and perfect binary trees, but these classifications do not inherently optimize search or insertion speeds.	Beyond the basic BST, variants such as AVL trees, Red-Black trees, and Splay trees are designed to maintain balance, ensuring consistently efficient operations.
Ease of Implementation	Generally simpler to implement since no additional constraints (like ordering) need to be maintained during insertion or deletion.	More complex due to the need to enforce and maintain the ordering property. Additional logic is required to ensure the tree remains balanced, especially in dynamic datasets.
Use Cases & Applications	Ideal for representing hierarchical data where order is irrelevant, such as parse trees, decision trees, or organizational structures.	Best suited for scenarios requiring efficient searching, sorting, and dynamic data management commonly used in database indexing, search algorithms, and real-time data lookup.
Memory Overhead	Each node typically stores data and pointers to two children; no extra metadata is needed to enforce order.	Similar memory usage per node; however, self-balancing variants might require additional data (such as balance factors or color flags) to maintain the structure.
Algorithm Complexity	Algorithms tend to be simpler due to the absence of order-based conditions, making implementation straightforward but potentially less efficient for searches.	Algorithms incorporate additional conditions to maintain the ordering property, which can increase complexity but results in more efficient searches and ordered data retrieval.

What Is A Binary Tree?

A binary tree is a hierarchical data structure where each node can have at most two children—commonly referred to as the left and right child. This simple yet versatile structure serves as the foundation for many advanced tree-based data structures and algorithms.

Components Of A Binary Tree

Root: The topmost node from which all other nodes descend.
Nodes: Individual elements containing data and pointers (or references) to their child nodes.
Edges: The connections between nodes, representing the relationship from parent to child.
Leaves: Nodes with no children, representing the end points of the tree.
Subtrees: Portions of the tree that themselves are binary trees.

Key Features Of Binary Tree

Hierarchical Organization: The tree structure naturally represents relationships, making it suitable for scenarios like organizational charts or file systems.
Flexibility: Binary trees do not impose any specific order among nodes. This makes them adaptable for various tasks where data ordering is not a priority.
Traversal Methods: Common traversal techniques (in-order, pre-order, post-order, and level-order) can be applied, each providing different perspectives on the data arrangement.
Dynamic Growth: Binary trees allow for dynamic insertion and deletion of nodes without the need for reordering the entire structure.

Visual Example Of A Binary Tree

Image of a binary tree

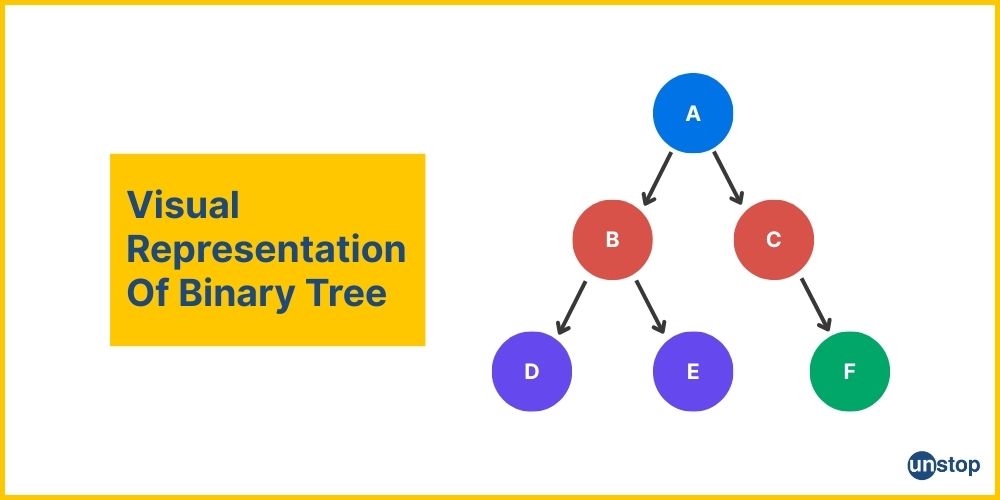
This diagram shows:

A as the root node.
B and C as the children of A.
D and E as children of B, and F as the right child of C.

Advantages & Disadvantages Of Binary Trees

Advantages	Disadvantages
Simplicity: Easy to implement and understand. Flexible Structure: Suitable for a wide range of applications, such as hierarchical data representation. Dynamic Growth: Nodes can be added or removed with minimal reorganization.	No inherent order: Lack of structure for efficient search operations. Inefficient Searches: May require traversing many nodes to locate a specific element (O(n) in the worst case). Memory Overhead: Each node requires extra storage for pointers or references.

What Is A Binary Search Tree?

A binary search tree (BST) is a specialized type of binary tree that organizes its nodes in a particular order to optimize search operations. In a BST, every node adheres to the following rule: all values in the left subtree are smaller than the node's value, and all values in the right subtree are larger. This property enables efficient data retrieval and helps maintain an ordered structure.

Components Of A Binary Search Tree

Root: The topmost node in the BST.
Nodes: Individual elements that contain data and pointers to their child nodes.
Edges: The connections that link nodes, representing parent-child relationships.
Leaves: Nodes that do not have any children.
Subtrees: Portions of the tree that themselves are valid BSTs, each following the same ordering rules.

Key Features Of A Binary Search Tree

Ordered Structure: The defining characteristic of a BST is its ordering property. This order ensures that an in-order traversal of the tree yields a sorted sequence of elements.
Efficient Searching: The ordering allows binary search techniques to be applied, enabling average-case search operations to be performed in O(log n) time when the tree is balanced.
Dynamic Operations: BSTs support dynamic insertion and deletion of nodes while maintaining the order, though additional operations may be necessary to rebalance the tree if it becomes skewed.
Traversal Methods: In-order traversal is particularly significant in BSTs, as it returns the elements in ascending order. Pre-order and post-order traversals can also be used for other specific purposes.

Visual Example Of A Binary Search Tree

Image of a binary search tree

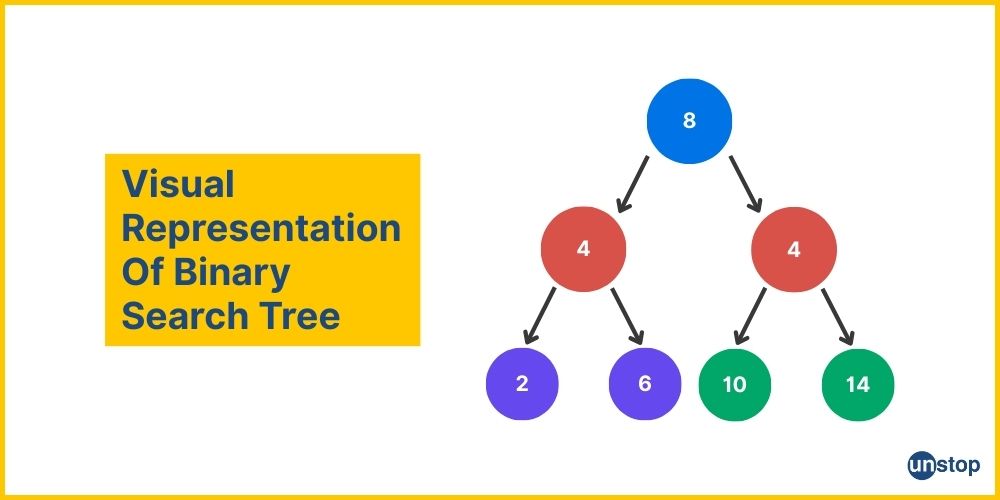
In this example:

8 is the root node.
4 and 12 are the left and right children of 8, respectively.
2 and 6 are the children of 4, while 10 and 14 are the children of 12.
Notice how each node adheres to the BST property: every node in the left subtree is less than the parent, and every node in the right subtree is greater.

Advantages & Disadvantages Of A Binary Search Tree

Advantages	Disadvantages
Efficient Searches: Fast lookup, insertion, and deletion in balanced trees. Ordered Data Retrieval: In-order traversal yields a sorted sequence. Dynamic Operations: Supports efficient dynamic updates to data.	Complexity: More complex to implement due to the ordering rules. Balancing Issues: Performance can degrade to O(n) if the tree becomes unbalanced. Maintenance Overhead: May require self-balancing techniques (like AVL or Red-Black trees) to maintain optimal performance.

Key Difference Between Binary Tree And Binary Search Tree Explained

While both data structures organize data hierarchically, the key difference lies in how they structure and manage data. Let’s break down the major distinctions:

Ordering & Structure | Binary Tree Vs. Binary Search Tree

Binary Tree: A binary tree imposes no strict order on its elements.

Nodes are added based solely on available positions rather than any value-based logic.
This results in a structure where the relative values of nodes are arbitrary.

Binary Search Tree (BST): A BST, in contrast, follows a precise ordering rule: for any given node, every node in its left subtree holds a value less than the node’s value, while every node in its right subtree holds a greater value. This inherent order organizes the tree in a way that supports efficient data retrieval.

Performance & Efficiency | Binary Tree Vs. Binary Search Tree

Search Operations:

Binary Tree: Since nodes aren’t ordered, searching may require examining each node, leading to a worst-case time complexity of O(n).
BST: The sorted structure allows binary search methods to be applied, achieving an average-case complexity of O(log n) when the tree is balanced. However, if the BST becomes unbalanced, performance can degrade to O(n).

Insertion and Deletion:

Binary Tree: Operations are generally straightforward because no ordering needs to be maintained.
BST: Insertions and deletions must preserve the tree’s ordering property, which often involves additional checks and sometimes re-balancing to maintain efficient performance.

Dynamic Operations & Maintenance | Binary Tree Vs. Binary Search Tree

Binary Tree: Flexible in terms of structure, binary trees are simple to implement and adjust.

They are excellent for representing hierarchical data where ordering isn’t a concern.
However, the lack of structure can lead to inefficiencies in search operations.

Binary Search Tree: The BST’s ordering property makes dynamic operations slightly more complex.

Each insertion or deletion must ensure that the tree remains ordered.
Additionally, self-balancing BST variants (such as AVL or Red-Black trees) may be used to automatically manage the tree’s balance and prevent performance degradation.

Practical Implications | Binary Tree Vs. Binary Search Tree

Binary Tree: Best suited for applications like organizational charts, parse trees, or any hierarchical data representation where fast search isn’t a priority.

Binary Search Tree: Ideal for scenarios requiring rapid lookup, insertion, and deletion, such as database indexing or implementing search algorithms.

Binary Tree Vs. Binary Search Tree | When To Use Which?

Choosing between a binary tree and a binary search tree depends on your specific application needs. The decision hinges on factors such as data organization, performance requirements, and the complexity you're willing to manage. Here is an overview of how these decision factors should influence your choice between the two:

Data Organization:

Binary Search Tree: Use a binary search tree if your application requires data to be stored in a sorted order. The inherent ordering of BSTs makes operations like searching, insertion, and deletion faster on average.
Binary Tree: Opt for a simple binary tree if you need to represent hierarchical relationships without the overhead of maintaining order.

Performance Needs:

Binary Search Tree: When fast lookups, dynamic insertions, and deletions are critical, the BST's ordered structure (especially when balanced) offers significant performance benefits.
Binary Tree: If your operations are more about traversing and representing data hierarchically—with less frequent search operations—the simpler structure of a binary tree might be sufficient.

Dynamic Data Handling:

Binary Search Tree: Ideal for applications with frequently changing datasets where maintaining order aids in quick access.
Binary Tree: Better suited for static or less dynamic data where maintaining order is not a priority.

Complexity vs. Simplicity:

Binary Search Tree: Although efficient, BSTs involve more complexity due to ordering rules and potential re-balancing requirements.
Binary Tree: Simpler to implement and manage, making them preferable when ease of development is a key consideration.

Visual Decision Flowchart

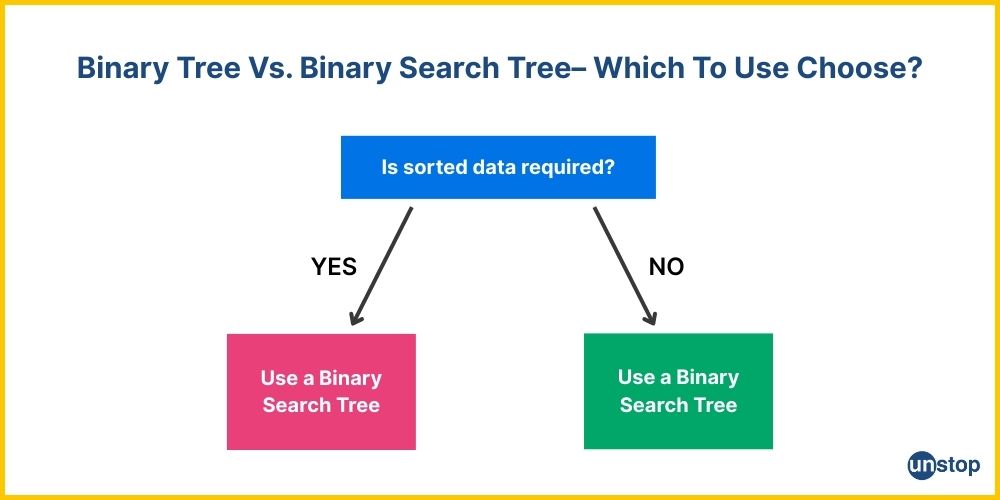
Which to choose– Binary tree vs. Binary search tree depending on sorted data

This flowchart illustrates that if your application demands sorted data for fast search operations, a BST is the way to go. Conversely, if the focus is on representing data hierarchically without ordering constraints, a binary tree is more appropriate.

Binary Tree Vs. Binary Search Tree Practical Applications | A Comparative Look

Both binary trees and binary search trees find their niches in real-world applications. Although they share a similar hierarchical structure, the choice between them often depends on specific requirements like data ordering, dynamic updates, and search efficiency. Below is a comparative overview of practical applications for each structure.

Application Area	Binary Tree	Binary Search Tree (BST)
Hierarchical Data Representation	Excellent for modeling relationships (e.g., org charts, file systems)	Less common if order isn't needed; used when data needs ordering
Search & Retrieval	Not optimized; typically requires full traversal (O(n))	Optimized for search with average O(log n) time in balanced trees
Dynamic Data Updates	Simple insertions/deletions without order constraints	Requires maintenance of order; self-balancing variants improve performance
Sorted Data Output	Traversals yield arbitrary sequences	In-order traversal produces a sorted sequence
Algorithmic & AI Applications	Useful in recursion, decision making, and parsing	Used in applications requiring rapid order-based access and updates

Applications Of Binary Trees

Hierarchical Representations: Ideal for modeling data that naturally forms a hierarchy. Examples include:

Organizational charts
File system directories
Parse trees in compilers

Decision Making and Recursion: Useful in algorithms that involve recursion or backtracking, such as:

Expression evaluation
Game tree exploration (e.g., decision trees in AI)

General-Purpose Data Storage: Used when the order of data isn’t critical and the primary goal is to represent parent-child relationships without imposing additional constraints.

Applications Of Binary Search Trees (BSTs)

Efficient Search and Retrieval: BSTs are favored when quick lookups, insertions, and deletions are required:

Database indexing
In-memory search operations in applications
Implementing ordered sets or maps

Dynamic Data Management: Their ordered structure makes BSTs particularly effective for applications where data is frequently updated:

Real-time data processing
Priority-based task scheduling

Sorted Data Output: In-order traversal of a BST yields a sorted list, making them useful in:

Sorting algorithms
Generating ordered reports or data streams

Comparative Visual Overview

Below is a flow diagram that summarizes the practical application scenarios for both structures:

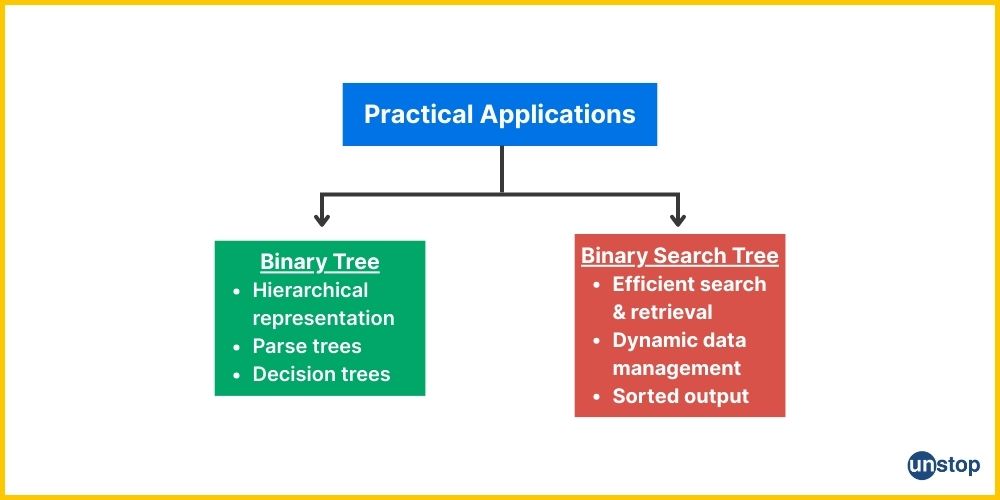
Practical applications– binary tree vs. binary search tree

Conclusion

Understanding the difference between a binary tree and a binary search tree is crucial when selecting the appropriate data structure for your application. A binary tree offers simplicity and flexibility for representing hierarchical data without the need for order, making it ideal for applications like organizational charts or parse trees. In contrast, a binary search tree leverages its ordered structure to provide efficient search, insertion, and deletion operations, which are essential for applications requiring dynamic data management and rapid lookups.

By comparing aspects such as structure, performance, and dynamic maintenance, you can determine which data structure best meets your needs. Ultimately, the decision hinges on whether your priority is straightforward hierarchical representation or optimized operations on ordered data.

Frequently Asked Questions

Q1. What is the main difference between a binary tree and a binary search tree?

A binary tree is a hierarchical structure where each node can have up to two children with no specific order, whereas a binary search tree (BST) enforces an order—each node’s left child must contain a value less than its own, and the right child must contain a greater value.

Q2. How does the ordering property affect search performance in BSTs compared to binary trees?

The ordering in a BST allows for binary search techniques, enabling faster average-case search operations (O(log n) when balanced) compared to the O(n) performance typically found in unordered binary trees.

Q3. When should I choose a binary tree over a BST?

Use a binary tree when your focus is on representing hierarchical data without needing fast, ordered searches. Opt for a BST if you require efficient lookup, insertion, and deletion operations, especially in applications that benefit from maintaining sorted data.

Q4. What are the common applications of binary search trees?

BSTs are widely used in database indexing, implementing ordered sets or maps, and scenarios where dynamic data management and rapid retrieval are crucial.

Q5. What are self-balancing BSTs and why are they important?

Self-balancing BSTs, such as AVL trees or Red-Black trees, automatically adjust their structure during insertions and deletions to maintain balance. This helps ensure that the tree remains efficient for search operations, preventing performance degradation in worst-case scenarios.

Q6. Can any binary tree be considered a BST?

No, only binary trees that adhere to the specific ordering rule (left child < parent < right child) qualify as binary search trees.

Q7. What are the key trade-offs between binary trees and BSTs?

Binary trees offer simplicity and flexibility, making them easy to implement and ideal for representing general hierarchical data. BSTs, however, provide ordered data and improved performance for search-related operations but require extra logic to maintain the order and balance.

This compiles our discussion on the difference between binary tree and binary search tree. Do check the following out:

Edited by

Shivani Goyal

Manager, Content

An economics graduate with a passion for storytelling, I thrive on crafting content that blends creativity with technical insight. At Unstop, I create in-depth, SEO-driven content that simplifies complex tech topics and covers a wide array of subjects, all designed to inform, engage, and inspire our readers. My goal is to empower others to truly #BeUnstoppable through content that resonates. When I’m not writing, you’ll find me immersed in art, food, or lost in a good book—constantly drawing inspiration from the world around me.

Tags:

Computer Science Engineering