- Linked List Interview Questions with Answers
53 Frequently Asked Linked List Interview Questions With Answers 2026

Linked list is one of the most important and basic concepts widely used in the computer science for many real-world applications. They are widely asked in technical interviews. Following are the top Linked list interview questions mostly asked across programming interviews.
Jobs for engineers! Check them out
Linked List Interview Questions with Answers
Q1. What is a Linked List?
Linked list is a basic data structure that is linear and recursive. Unlike arrays, it is a linked data structure. Linked lists consist of nodes. Every node has two elements - value and a pointer that points to the next node or Null. The first node of the linked list is called the head while the last node is called the tail. The following image will help to understand better.

There are several types of linked lists, each designed to suit specific requirements and use cases. Here are some common types of linked lists:
- Singly Linked List
- Doubly Linked List
- Circular Linked List
- Doubly Circular Linked List
- Skip List
- Self-Organizing List
- Unrolled Linked List
- XOR Linked List
Note: There are no pointers in JavaScript (unlike languages like C++). In JavaScript, you work with references instead of pointers. While references and pointers serve similar purposes, they have some differences due to JavaScript's memory management model.
Q2. What are the differences between array data structure and linked list data structure?
The following is the comparison between array and linked list data structure:
Linked List |
Array |
| Linked lists store elements in a linked manner. | Array stores elements in a contiguous memory location. |
| It does not require pre-allocation of memory. | It requires pre-allocation of memory. |
| Very less or no memory wastage. | There is memory wastage in arrays. |
| Insertion and deletion is less costly operation as compared to arrays. | Insertion and deletion in arrays is more costly operations as compared to Linked lists. |
| To access an element we need to traverse till that element in the linked list and hence is a O(n) operation, i.e., more time complexity .The access time is more.We cannot access any kth node directly. | Access in arrays is done using indexes and hence is a O(1) operation, i.e., lesser time complexity (Constant Time). |
| Size of linked list can be extended or reduced as per requirement. It can change size at runtime. | Size of Array cannot be extended or reduced as per requirement. |
Q3. What does the node of a LinkedList consist of?
A node is the basic building block of a linked list. The node of a linked list consists of data and the address of the next node (pointer or reference).
Q4. What are the different types of Linked Lists?
The following are the types of Linked Lists:
- Singly Linked List
- Doubly Linked List
- Circular Linked List
- Multiply Linked List
Q5. What is a Singly Linked List?
A Singly Linked List contains of nodes which have the data and address of the next node. The last node i.e., the tail pointer, in the Singly Linked List points to NULL.
The following diagram depicts a singly linked list:
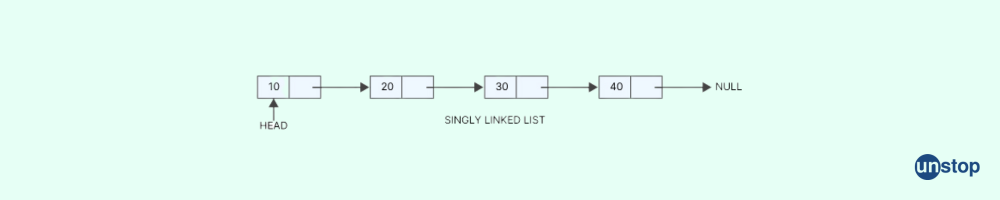
Q6. What is a Doubly Linked List?
A Doubly Linked List contains of nodes which have the data , address of the next node as well as address of the previous node. The last node in the Doubly Linked List points to NULL. Also the previous address of the of the first node i.e, the head node , in the doubly linked list points to NULL.
The following diagram depicts a doubly linked list:
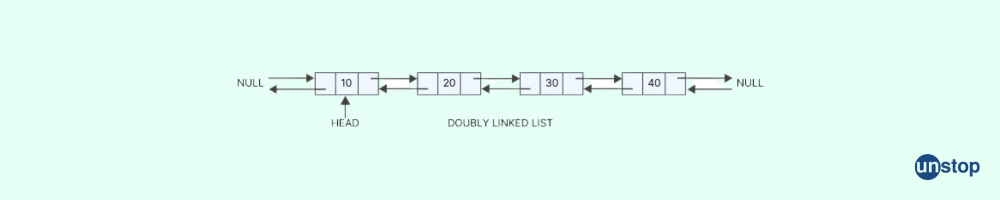
Q7. What is a Circular Linked List?
A Circular Linked List contains of nodes which have the data and address of the next node. The last node in the Singly Linked List points to the first node i.e., the last node in a circular linked list holds the address of the first node i.e., the head node.
The following diagram depicts a circular linked list:
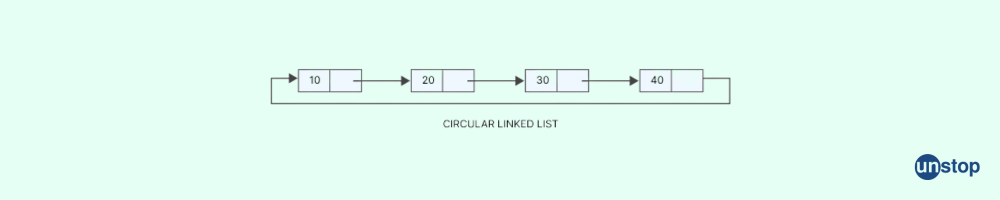
Q8. Which type of memory allocation is done in case of LinkedList?
In the case of Linked Lists, dynamic memory allocation is done,i.e., memory is allocated at runtime or as per requirement.
The reason for such allocation is that the basic unit of a Linked List is a node. Each node has some data and address to the next node. Now, if allocation is static, the length of the Linked List would be fixed which is not the case with Linked Lists. Hence, dynamic allocation of memory means that allocation of nodes takes place at runtime and hence, the length of the Linked List can change.
Q9. What are the applications of Linked Lists?
Linked Lists has a wide variety of applications. Many data structures like stack and queue use Linked Lists in their internal implementation. Other applications of Linked Lists are:
- In the data structures like binary trees, hash tables to handle collisions, etc.
- Linked lists can be used to manage memory allocation and deallocation in systems.
- To create music playlists.
- To implement undo and redo functionality in applications
- In blockchain technology
Q10. Which package contains Linked List in Java?
Linked List is a part of the Collection framework present in java.util package. This class is an implementation of the Linked List data structure which is a linear data structure where the elements are not stored in contiguous locations and every element is a separate object with a data part and address part.
Q11. What are advantages of Linked Lists?
The following are the advantages of Linked List:
- It does not require pre-allocation of memory. Hence it need not be any of any flexible size and can be extended as and when required.
- The basic operations like Insertion and deletion of elements is easier in Linked Lists as compared to arrays.
- There is less or no wastage of space in Linked List.
Q12. What are disadvantages of Linked Lists?
The following are the disadvantages of Linked Lists:
- Random access of elements is not possible in Linked Lists. To access an element we need to traverse till that element in the Linked List and hence is a O(n) operation.
- More memory space is required in Linked Lists as along with data , address of the next nodes is also stored.
- Linked Lists provide for poor locality and the memory used in Linked list is scattered as it is not stored at contiguous memory locations.
Q13. How do you insert a node at the front of a singly linked list?
To insert a node at the front in the linkedlist , we create a new node named temp having the data value x. If head of the linkedlist is null, head is assigned to newly created node temp. Else temp’s next points to head and head is assigned to temp. and finally head is returned. The following code sample shows the function to insert a node at the front in the LinkedList.
CODE SNIPPET IS HEREIAogICAgICAgICAgTm9kZSBpbnNlcnRBdEJlZ2lubmluZyhOb2RlIGhlYWQsIGludCB4KQogICAgewoKICAgICAgICBOb2RlIHRlbXA9bmV3IE5vZGUoeCk7ICAvL2NyZWF0aW5nIGEgdGVtcG9yYXJ5IG5vZGUgd2l0aCBkYXRhIHgKCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIC8qIElmIGhlYWQgaXMgbnVsbCB0aGVuIHdlIGFzc2lnbiBoZWFkIHRvIHRlbXAgKi8KICAgICAgICBpZihoZWFkPT1udWxsKQogICAgICAgIGhlYWQ9dGVtcDsKCmVsc2UgICAgCgovKiBJZiBoZWFkIGlzIG5vdCBudWxsIHdlIGFzc2lnbiB0ZW1wJ3MgbmV4dCB0byBoZWFkIGFuZCB0aGVuIG1ha2UgaGVhZD10ZW1wICovCnsKICAgICAgICB0ZW1wLm5leHQ9aGVhZDsKICAgICAgICBoZWFkPXRlbXA7CiAgICB9CnJldHVybiBoZWFkOwp9CiAgICAgICAgIA==
Q14. How do you insert a node at the end of a singly linked list?
To insert a node at the end in the Linked List , we create a new node named temp having the data value x. If head of the Linked List is null, head is assigned to newly created node temp. Else we traverse the linkedlist till we get the hold of the last node in the linkedlist. Now, current's next points to temp and temp’s next points to NULL and finally head is returned. The following code shows the function to insert a node at the end in the LinkedList.
CODE SNIPPET IS HERETm9kZSBpbnNlcnRBdEVuZChOb2RlIGhlYWQsIGludCB4KQogICAgewogICAgICAgIE5vZGUgdGVtcD1uZXcgTm9kZSh4KTsgLy9jcmVhdGluZyBhIHRlbXBvcmFyeSBub2RlIHdpdGggZGF0YSB4CgogICAgICAgIC8qIElmIGhlYWQgaXMgbnVsbCAsIHRoZW4gYXNzaWduaW5nIGhlYWQgdG8gdGVtcCovCgogICAgICAgIGlmKGhlYWQ9PW51bGwpCiAgICAgICAgaGVhZD10ZW1wOwoKLyogRWxzZSBjdXJyIG5vZGUgaXMgYXNzaWduZWQgdG8gaGVhZCBhbmQgd2UgdHJhdmVyc2UgdGhlIGxpbmtlZGxpc3QgdGlsbCBjdXJyZW50J3MgbmV4dCBpcyBub3QgbnVsbCovCgogICAgICAgIE5vZGUgY3Vycj1oZWFkOwogICAgICAgIHdoaWxlKGN1cnIubmV4dCE9bnVsbCl7CiAgICAgICAgICAgIGN1cnI9Y3Vyci5uZXh0OwogICAgICAgIH0KLypOb3cgd2UgaGF2ZSB0aGUgaG9sZCBvZiBsYXN0IGVsZW1lbnQgaW4gdGhlIExpbmtlZExpc3QgLCBub3cgd2UgYXNzaWduIGN1cnJlbnQncyBuZXh0IHRvIHRlbXAgYW5kIG1ha2UgdGVtcCdzIG5leHQgcG9pbnQgdG8gbnVsbCovCiAgICAgICAgCiAgICAgICAgY3Vyci5uZXh0PXRlbXA7CiAgICAgICAgdGVtcC5uZXh0PW51bGw7CiAgICAgICAgCiAgICAgICAgLy8gcmV0dXJuaW5nIGhlYWQgb2YgdGhlIGxpbmtlZGxpc3QKICAgICAgICByZXR1cm4gaGVhZDsKfQ==
Q15. How do you delete a node at the front, i.e. leftmost node, of a singly linked list?
Basically to delete a node from the front of the LinkedList, we first check if the head node is null and it it is null, we return null. Else if there are nodes in the LinkedList, we just make head point to head's next and return the new head. The following is the code to delete a node from the front of a singly linkedlist.
CODE SNIPPET IS HEREICBOb2RlIHJlbW92ZUZpcnN0Tm9kZShOb2RlIGhlYWQpewoKaWYoaGVhZD09bnVsbCkKCnJldHVybiBudWxsOwoKLy9Nb3ZlIHRoZSBoZWFkIHBvaW50ZXIgdG8gdGhlIG5leHQgbm9kZQoKTm9kZSB0ZW1wPWhlYWQ7CgpoZWFkPWhlYWQubmV4dDsKCnJldHVybiBoZWFkOwoKfQog
Q16. How do you delete a node at the end of a singly linked list?
Basically to delete a node from the end of the LinkedList, we first check if the head node is null and it it is null, we return null. Otherwise, we traverse till the second last element and finally, we make second last element 's next as null, thus deleting the last element from the singly LinkedList The following is the code to delete a node from the end of a singly linkedlist.
CODE SNIPPET IS HERETm9kZSByZW1vdmVMYXN0Tm9kZShOb2RlIGhlYWQpCnsKICAgIGlmIChoZWFkID09IG51bGwpCiAgICAgICAgcmV0dXJuIG51bGw7CgogICAgaWYgKGhlYWQubmV4dCA9PSBudWxsKSB7CiAgICAgICAgcmV0dXJuIG51bGw7CiAgICB9CgogICAgLy8gRmluZCB0aGUgc2Vjb25kIGxhc3Qgbm9kZQogICAgTm9kZSBzZWNvbmRfbGFzdCA9IGhlYWQ7CiAgICB3aGlsZSAoc2Vjb25kX2xhc3QubmV4dC5uZXh0ICE9IG51bGwpCiAgICAgICAgc2Vjb25kX2xhc3QgPSBzZWNvbmRfbGFzdC5uZXh0OwoKICAgIC8vIENoYW5nZSBuZXh0IG9mIHNlY29uZCBsYXN0CiAgICBzZWNvbmRfbGFzdC5uZXh0ID0gbnVsbDsKCiAgICByZXR1cm4gaGVhZDsKfQ==
Q17. How do you reverse a linked list ?
The following function shows the code sample to reverse a LinkedList:
CODE SNIPPET IS HERECiAgICAgICAgICBOb2RlIHJldmVyc2VMaXN0KE5vZGUgaGVhZCkKICAgIHsKICAgICAgICBOb2RlIGN1cnI9aGVhZCxwcmV2PW51bGw7ICAvL2luaXRpYWxpemluZyBjdXJyIHRvIGhlYWQgYW5kIHByZXYgdG8gbnVsbAoKICAgICAvKiB3aGlsZSBjdXJyIGlzIG5vdCBudWxsIHdlIGRvIHRoZSBmb2xsb3dpbmcgb3BlcmF0aW9uczoKICAgICAgMS4gV2UgYXNzaWduIGN1cnIncyBuZXh0IHRvIG5leHQuCiAgICAgIDIuTWFrZSBjdXJyLm5leHQgcG9pbnQgdG8gcHJldgogICAgICAzLlBvaW50IHByZXYgdG8gY3VycgogICAgICA0LlBvaW50IGN1cnIgdG8gbmV4dCovCgogd2hpbGUoY3VyciE9bnVsbCl7CiAgICAgIE5vZGUgbmV4dD1jdXJyLm5leHQ7CiAgICAgIGN1cnIubmV4dD1wcmV2OwogICAgICBwcmV2PWN1cnI7CiAgICAgIGN1cnI9bmV4dDsKICAgICAgICAgICAgICB9CiAgICAgICAgcmV0dXJuIHByZXY7IC8vcmV0dXJuIHByZXYKICAgICAgICAKICAgICAgICB9IA==
Q18. How do you print the data present in the nodes, i.e. List nodes, of a singly linked List?
To print the data present in the nodes of the linked list , we traverse the LinkedList until the current node is pointing to NULL. During the traversal of the LinkedList , we print current data at each iteration and then point curr to curr.next. In this way all the nodes of the LinkedList are printed.
CODE SNIPPET IS HEREcHVibGljIHN0YXRpYyB2b2lkIHByaW50U2luZ2x5TGlua2VkTGlzdChOb2RlIGhlYWQpewoKICAgIE5vZGUgY3Vycj1oZWFkOyAvL2N1cnJlbnQgbm9kZSBpcyBpbnRpYWxpemVkIHRvIGhlYWQKCiAgICAvKiBpdGVyYXRpbmcgdGlsbCB0aGUgY3VyciB2YWx1ZSBkb2VzIG5vdCBiZWNvbWUgbnVsbCAqLwogICAgd2hpbGUoY3VyciE9bnVsbCkKICAgIHsKICAgICBTeXN0ZW0ub3V0LnByaW50bG4oY3Vyci5kYXRhKTsgLy9wcmludGluZyB0aGUgY3VycidzIGRhdGEgYXQgZWFjaCBpdGVyYXRpb24KICAgIGN1cnI9Y3Vyci5uZXh0OwogICAgfQoKfQ==
The above function prints the data in the nodes of the LinkedList.
Q19. How do you calculate the length of a singly linked List?
To calculate the length of the linked list , we traverse the LinkedList until the current node is pointing to NULL. During the traversal of the LinkedList , we keep a counter and increment it in each iteration. The value of the counter at the end of the iteration is the length of the LinkedList. So, List traversal can help in finding the length of a singly LinkedList by keeping a count variable.
The function to calculate the length of the singly LinkedList is written below:
CODE SNIPPET IS HEREcHVibGljIHN0YXRpYyBpbnQgZ2V0Q291bnQoTm9kZSBoZWFkKQogICAgewogICAgICAgIGludCBjPTA7IC8vY291bnRlciBpbml0aWFsaXplZCB0byAwCgogICBOb2RlIGN1cnI9aGVhZDsgLy9jdXJyZW50IG5vZGUgaXMgaW50aWFsaXplZCB0byBoZWFkCgogICAgICAgIC8qIGl0ZXJhdGluZyB0aWxsIHRoZSBjdXJyIHZhbHVlIGRvZXMgbm90IGJlY29tZSBudWxsICovCgogICAgICAgIHdoaWxlKGN1cnIhPW51bGwpCiAgICAgICAgewogICAgICAgIGMrKzsgLy9pbmNyZW1lbnRpbmcgdGhlIGNvdW50ZXIgYXQgZWFjaCBpdGVyYXRpb24KICAgICAgICBjdXJyPWN1cnIubmV4dDsKICAgICAgICB9CiAgICAgICAgcmV0dXJuIGM7CgogICAgfQ==
The above function calculates the number of nodes in the LinkedList.
Q20. Differentiate between Singly and Doubly LinkedList.
The following is he difference between Singly and Doubly Linked List:
|
SINGLY LINKED LIST |
DOUBLY LINKED LIST |
| Stores data and address of the next node. | Each node has address of the previous and next node. |
| Requires less extra space as compared to a Doubly Linked List. | Requires extra space as compared to a Singly LinkedList, hence has more space complexity. |
| Implementation is easy as compared to a Doubly LinkedList because of less space complexity than Doubly LinkedList.. | Implementation is difficult as compared to a Singly LinkedList because of more space complexity. |
Q21. What does the dummy header in the linked list contain?
Dummy header consists of the first record of the actual data in a LinkedList. It is created to contain the first record. Now, initially, there is no node which is pointing to the first node. So, we create a dummy node which is the dummy header, which points to the first record of the actual data in the LinkedList.Using the dummy header, we can do all the operations on the LinkedList, like, traversing the linkedlist, finding middle of the LinkedList, etc.
Q22. How do you find the middle node in the linked list?
To find middle node in the linked list, we use two pointer approach. We take two pointers, slow pointer and fast pointer. Initially, both slow pointer and fast pointer are intiailized to head. Then the slow pointer moves one space ahead at a time whereas the fast pointer moves two pointers ahead at time and the traversal continues till fast pointer does not point to null or fast pointer's next does not point to null.The algorithm takes care of odd node list as well as even node list. The following is the function to find the middle node in the LinkedList:
CODE SNIPPET IS HEREcHVibGljIHN0YXRpYyBpbnQgZ2V0Q291bnQoTm9kZSBoZWFkKQogICAgewogICAgICAgIGludCBjPTA7IC8vY291bnRlciBpbml0aWFsaXplZCB0byAwCgogICBOb2RlIGN1cnI9aGVhZDsgLy9jdXJyZW50IG5vZGUgaXMgaW50aWFsaXplZCB0byBoZWFkCgogICAgICAgIC8qIGl0ZXJhdGluZyB0aWxsIHRoZSBjdXJyIHZhbHVlIGRvZXMgbm90IGJlY29tZSBudWxsICovCgogICAgICAgIHdoaWxlKGN1cnIhPW51bGwpCiAgICAgICAgewogICAgICAgIGMrKzsgLy9pbmNyZW1lbnRpbmcgdGhlIGNvdW50ZXIgYXQgZWFjaCBpdGVyYXRpb24KICAgICAgICBjdXJyPWN1cnIubmV4dDsKICAgICAgICB9CiAgICAgICAgcmV0dXJuIGM7CgogICAgfQ==
Q23. How do you delete the middle element of Linked List?
To find middle node in the linked list ,we use two pointer approach. We take two pointers, slow pointer and fast pointer. Initially, both slow pointer and fast pointer are intiailized to head. Then the slow pointer moves one space ahead at a time whereas the fast pointer moves two pointers ahead at time and the traversal continues till fast pointer does not point to null or fast pointer's next does not point to null to keep into mid odd node list as well as even node list.
When either of the cases occur, that is the middle node of the LinkedList. Now, in addition to the above process, we keep an extra pointer named prev. Using prev (previous pointer) we keep the track of the previous node of the middle node. At last we just point prev's next to slow.next. That will delete the middle element of the LinkedList irrespective of the LinkedList having odd nodes or even number of nodes. The following is the function to delete the middle node in the LinkedList:
CODE SNIPPET IS HEREIE5vZGUgZGVsZXRlTWlkKE5vZGUgaGVhZCkgewoKIC8qSWYgaGVhZCBpcyBudWxsIHdlIHJldHVybiBudWxsKi8KICAgICAgICAgaWYoaGVhZD09bnVsbCkKICAgICAgICAgIHJldHVybiBudWxsOwoKICAgICAgICAgIC8qSWYgaGVhZCdzIG5leHQgaXMgbnVsbCB0aGVuIHdlIHJldHVybiBudWxsKi8KICAgICAgICBpZihoZWFkLm5leHQ9PW51bGwpCiAgICAgICAgICAgIHJldHVybiBudWxsOwoKICAgIC8qV2Uga2VlcCBvbmUgZXh0cmEgcG9pbnRlciBpbiBhZGRpdGlvbiB0byBzbG93IGFuZCBmYXN0IHBvaW50ZXJzIGhlcmUsaS5lLiwgcHJldmlvdXMgcG9pbnRlciwgd2hpY2gga2VlcHMgdGhlIHRyYWNrIG9mIHByZXYgZWxlbWVudCBvZiB0aGUgbWlkZGxlIGVsZW1lbnQqLyAgICAgICAgCgogICAgICAgIE5vZGUgcHJldj1oZWFkOwogICAgICAgIE5vZGUgc2xvdz1oZWFkLGZhc3Q9aGVhZDsKICAgICAgICB3aGlsZShmYXN0IT1udWxsJiZmYXN0Lm5leHQhPW51bGwpewogICAgICAgICAgICBwcmV2PXNsb3c7CiAgICAgICAgICAgIHNsb3c9c2xvdy5uZXh0OwogICAgICAgICAgICBmYXN0PWZhc3QubmV4dC5uZXh0OwogICAgICAgIH0KICAgICAgIHByZXYubmV4dD1zbG93Lm5leHQ7IC8vcG9pbnRpbmcgcHJldidzIG5leHQgdG8gc2xvdydzIG5leHQKICAgICAgICByZXR1cm4gaGVhZDsgLy9yZXR1cm5pbmcgaGVhZAogICAgfQogICAgICAgIA==
Q24. How do you detect if there is a cycle in the Linked List?
To find if there is a cycle in the linkedlist ,we use two pointer approach. We take two pointers, slow pointer and fast pointer. Initially, both slow pointer and fast pointer are intiailized to head. Then the slow pointer moves one space ahead at a time whereas the fast pointer moves two pointers ahead at time and the traversal continues till fast pointer does not point to null or fast pointer's next does not point to null. When either of the cases occur, it means that there is no cycle in the List.
But if at some point in the traversal slow and fast become equal, it means that there is a cycle and we return true. It is know as the Floyd's Cycle-Finding Algorithm. The following is the function to find if there is a cycle in the LinkedList:
CODE SNIPPET IS HEREcHVibGljIHN0YXRpYyBib29sZWFuIGRldGVjdExvb3AoTm9kZSBoZWFkKXsKICAgICAgICBOb2RlIHNsb3c9aGVhZCxmYXN0PWhlYWQ7Ly9zbG93IGFuZCBmYXN0IHBvaW50ZXJzIGFyZSBpbnRpdGlhbGl6ZWQgdG8gaGVhZAogICAgICAgIC8qV2UgdXNlIHR3byBwb2ludGVyIG1ldGhvZCB0byBkZXRlY3QgbG9vcCovCiAgICAgICAgd2hpbGUoZmFzdCE9bnVsbCYmZmFzdC5uZXh0IT1udWxsKXsKICAgICAgICAgICAgc2xvdz1zbG93Lm5leHQ7CiAgICAgICAgICAgIGZhc3Q9ZmFzdC5uZXh0Lm5leHQ7CiAgICAgICAgICAgIC8qSWYgc2xvdyBiZWNvbWVzIGVxdWFsIHRvIGZhc3QsIGl0IG1lYW5zIHRoZXJlIGlzIGEgbG9vcCBhbmQgd2UgcmV0dXJuIHRydWUqLwogICAgICAgICAgICAgaWYoc2xvdz09ZmFzdCkKICAgICAgICAgICAgcmV0dXJuIHRydWU7CiAgICAgICAgfQogICAgICAgICAgICByZXR1cm4gZmFsc2U7CiAgICAgICAgCiAgICB9
Q25. How do you delete a node with only pointer given to it?
To delete a node with the only pointer given to it, we store the next node's data in the current node and then we point the current node to current node's next's next. The following is the function to delete a node with the only pointer given to it:
CODE SNIPPET IS HEREdm9pZCBkZWxldGVOb2RlKE5vZGUgZGVsKQogICAgewogICAgICAgICBkZWwuZGF0YT1kZWwubmV4dC5kYXRhOyAKICAgICAgICAgZGVsLm5leHQ9ZGVsLm5leHQubmV4dDsKICAgIH0KIA==
Q26. What is the time complexity to access kth element in a Singly Linked List?
The time complexity to access kth element in a Singly LinkedList is O(N) .To access the Kth element in the list ,first step is to traverse till the kth element and then access the element .So, to traverse the list till we get the Kth element is a O(N) operation and then accessing the element is O(1) operation. Hence the total time complexity to access the kth element is O(N)+O(1)=O(N).
SOURCE CODE:
CODE SNIPPET IS HEREICAvKiBUYWtlcyBpbmRleCBhcyBhcmd1bWVudCBhbmQgcmV0dXJuIGRhdGEgYXQgaW5kZXgqLwpwdWJsaWMgaW50IEdldE50aChpbnQgaW5kZXgsIE5vZGUgaGVhZCkKewogICAgTm9kZSBjdXJyZW50ID0gaGVhZDsKICAgIGludCBjb3VudCA9IDA7IC8vIGluZGV4IG9mIE5vZGUgd2UgYXJlIGN1cnJlbnRseSBsb29raW5nCiAgICB3aGlsZSAoY3VycmVudCAhPSBudWxsKQogICAgewogICAgICAgIGlmIChjb3VudCA9PSBpbmRleCkKICAgICAgICAgICAgcmV0dXJuIGN1cnJlbnQuZGF0YTsKICAgICAgICBjb3VudCsrOwogICAgICAgIGN1cnJlbnQgPSBjdXJyZW50Lm5leHQ7CiAgICB9CiAgICByZXR1cm4gMDsKfSA=
Q27. What is the time complexity to traverse all the elements in a Singly Linked List?
The time complexity to traverse all the elements in a Singly LinkedList is O(N) .To traverse all the elements in Singly Linked List means passing through each and every node in the LinkedList and then accessing the data using curr.data. Now, to traverse the LinkedList we need to loop through the entire length of the loop till the node points to NULL and each time print the data. So that is a O(N) operation. Hence the total time complexity is O(N),i.e., linear time.
SOURCE CODE:
CODE SNIPPET IS HEREICBwdWJsaWMgc3RhdGljIHZvaWQgcHJpbnRTaW5nbHlMaW5rZWRMaXN0KE5vZGUgaGVhZCl7CgogICAgTm9kZSBjdXJyPWhlYWQ7IC8vY3VycmVudCBub2RlIGlzIGludGlhbGl6ZWQgdG8gaGVhZAoKICAgIC8qIGl0ZXJhdGluZyB0aWxsIHRoZSBjdXJyIHZhbHVlIGRvZXMgbm90IGJlY29tZSBudWxsICovCiAgICB3aGlsZShjdXJyIT1udWxsKQogICAgewogICAgIFN5c3RlbS5vdXQucHJpbnRsbihjdXJyLmRhdGEpOyAvL3ByaW50aW5nIHRoZSBjdXJyJ3MgZGF0YSBhdCBlYWNoIGl0ZXJhdGlvbgogICAgY3Vycj1jdXJyLm5leHQ7CiAgICB9Cgp9IA==
The above function prints the data in the nodes of the Linked List.
Q28. What is the time complexity to insert an element at any position in a Singly LinkedList?
The time complexity to insert an element at any position in a Singly LinkedList is O(N) .To insert a element at any position , first step is to reach till that position. So, to reach till that position we will need to traverse the LinkedList, and reach that position which is in worst case O(N) operation . Now , we will require the previous node’s reference and that previous node’s pointer we will need to assign to curr pointer and curr’s next to prev pointer’s next which is a O(1) operation. So, in all the total time complexity is O(N)+O(1)=O(N).
SOURCE CODE:
CODE SNIPPET IS HERELy8gZnVuY3Rpb24gdG8gaW5zZXJ0IGEgTm9kZSBhdCByZXF1aXJlZCBwb3NpdGlvbgoKc3RhdGljIE5vZGUgSW5zZXJ0UG9zKE5vZGUgaGVhZE5vZGUsIGludCBwb3NpdGlvbiwgaW50IGRhdGEpIHsKCk5vZGUgaGVhZCA9IGhlYWROb2RlOwoKaWYgKHBvc2l0aW9uIDwgMSkKClN5c3RlbS5vdXQucHJpbnQoIkludmFsaWQgcG9zaXRpb24iKTsKCi8vIGlmIHBvc2l0aW9uIGlzIDEgdGhlbiBuZXcgbm9kZSBpcwoKLy8gc2V0IGluZnJvbnQgb2YgaGVhZCBub2RlCgovLyBoZWFkIG5vZGUgaXMgY2hhbmdpbmcuCgppZiAocG9zaXRpb24gPT0gMSkgewoKTm9kZSBuZXdOb2RlID0gbmV3IE5vZGUoZGF0YSk7CgpuZXdOb2RlLm5leHROb2RlID0gaGVhZE5vZGU7CgpoZWFkID0gbmV3Tm9kZTsKCn0gZWxzZSB7Cgp3aGlsZSAocG9zaXRpb24tLSAhPSAwKSB7CgppZiAocG9zaXRpb24gPT0gMSkgewoKLy8gYWRkaW5nIE5vZGUgYXQgcmVxdWlyZWQgcG9zaXRpb24KCk5vZGUgbmV3Tm9kZSA9IEdldE5vZGUoZGF0YSk7CgovLyBNYWtpbmcgdGhlIG5ldyBOb2RlIHRvIHBvaW50IHRvCgovLyB0aGUgb2xkIE5vZGUgYXQgdGhlIHNhbWUgcG9zaXRpb24KCm5ld05vZGUubmV4dE5vZGUgPSBoZWFkTm9kZS5uZXh0Tm9kZTsKCi8vIFJlcGxhY2luZyBjdXJyZW50IHdpdGggbmV3IE5vZGUKCi8vIHRvIHRoZSBvbGQgTm9kZSB0byBwb2ludCB0byB0aGUgbmV3IE5vZGUKCmhlYWROb2RlLm5leHROb2RlID0gbmV3Tm9kZTsKCmJyZWFrOwoKfQoKaGVhZE5vZGUgPSBoZWFkTm9kZS5uZXh0Tm9kZTsKCn0KCmlmIChwb3NpdGlvbiAhPSAxKQoKU3lzdGVtLm91dC5wcmludCgiUG9zaXRpb24gb3V0IG9mIHJhbmdlIik7Cgp9CgpyZXR1cm4gaGVhZDsKCn0=
Q29. What is the time complexity to delete an element at any position in a Singly Linked List?
The time complexity to delete an element at any position in a Singly LinkedList is O(N) .To delete an element at any position , first step is to reach till that position. So, to reach till that position we will need to traverse the LinkedList, and reach that position which is in worst case O(N) operation . Now , we will require the previous node’s reference and that previous node’s pointer we will need to assign to curr’s next which is a O(1) operation. So, in all the total time complexity is O(N)+O(1)=O(N).
SOURCE CODE:
CODE SNIPPET IS HEREICB2b2lkIGRlbGV0ZU5vZGUoaW50IHBvc2l0aW9uKQp7CiAgICAvLyBJZiBsaW5rZWQgbGlzdCBpcyBlbXB0eQogICAgaWYgKGhlYWQgPT0gbnVsbCkKICAgICAgICByZXR1cm47CgogICAgLy8gU3RvcmUgaGVhZCBub2RlCiAgICBOb2RlIHRlbXAgPSBoZWFkOwoKICAgIC8vIElmIGhlYWQgbmVlZHMgdG8gYmUgcmVtb3ZlZAogICAgaWYgKHBvc2l0aW9uID09IDApIHsKICAgICAgICBoZWFkID0gdGVtcC5uZXh0OyAvLyBDaGFuZ2UgaGVhZAogICAgICAgIHJldHVybjsKICAgIH0KCiAgICAvLyBGaW5kIHByZXZpb3VzIG5vZGUgb2YgdGhlIG5vZGUgdG8gYmUgZGVsZXRlZAogICAgZm9yIChpbnQgaSA9IDA7IHRlbXAgIT0gbnVsbCAmJiBpIDwgcG9zaXRpb24gLSAxOwogICAgICAgIGkrKykKICAgICAgICB0ZW1wID0gdGVtcC5uZXh0OwoKICAgIC8vIElmIHBvc2l0aW9uIGlzIG1vcmUgdGhhbiBudW1iZXIgb2Ygbm9kZXMKICAgIGlmICh0ZW1wID09IG51bGwgfHwgdGVtcC5uZXh0ID09IG51bGwpCiAgICAgICAgcmV0dXJuOwoKICAgIC8vIE5vZGUgdGVtcC0+bmV4dCBpcyB0aGUgbm9kZSB0byBiZSBkZWxldGVkCiAgICAvLyBTdG9yZSBwb2ludGVyIHRvIHRoZSBuZXh0IG9mIG5vZGUgdG8gYmUgZGVsZXRlZAoKICAgIE5vZGUgbmV4dCA9IHRlbXAubmV4dC5uZXh0OwoKICAgIHRlbXAubmV4dD0gbmV4dDsgLy8gVW5saW5rIHRoZSBkZWxldGVkIG5vZGUgZnJvbSBsaXN0Cn19IA==
Q30. What is the time complexity to insert an element at front position in a Singly LinkedList?
The time complexity to insert an element at front position in a Singly LinkedList is O(1) .To insert a node at the front in the Linked List , we create a new node named temp having the data value x. If head of the Linked List is null, head is assigned to newly created node temp. Else temp’s next points to head and head is assigned to temp. and finally head is returned. So, here no traversal of LinkedList is required.Only changing of links is required and that is a O(1) operation.
SOURCE CODE:
CODE SNIPPET IS HEREICBOb2RlIGluc2VydEF0QmVnaW5uaW5nKE5vZGUgaGVhZCwgaW50IHgpCiAgICB7CgogICAgICAgIE5vZGUgdGVtcD1uZXcgTm9kZSh4KTsgIC8vY3JlYXRpbmcgYSB0ZW1wb3Jhcnkgbm9kZSB3aXRoIGRhdGEgeAoKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgLyogSWYgaGVhZCBpcyBudWxsIHRoZW4gd2UgYXNzaWduIGhlYWQgdG8gdGVtcCAqLwogICAgICAgIGlmKGhlYWQ9PW51bGwpCiAgICAgICAgaGVhZD10ZW1wOwoKZWxzZSAgICAKCi8qIElmIGhlYWQgaXMgbm90IG51bGwgd2UgYXNzaWduIHRlbXAncyBuZXh0IHRvIGhlYWQgYW5kIHRoZW4gbWFrZSBoZWFkPXRlbXAgKi8KewogICAgICAgIHRlbXAubmV4dD1oZWFkOwogICAgICAgIGhlYWQ9dGVtcDsKICAgIH0KcmV0dXJuIGhlYWQ7Cn0g
Q31. What is the time complexity to insert an element at end position in a Singly LinkedList?
The time complexity to insert an element at end position in a Singly LinkedList is O(N) . To insert a node at the end in the Linked List , we create a new node named temp having the data value x. If head of the Linked List is null, head is assigned to newly created node temp.
Else we traverse the linkedlist till we get the hold of the last node in the linkedlist. Now, current's next points to temp and temp’s next points to NULL and finally head is returned. So, we first need to traverse the linkedlist till the last node is reached and then assign curr’s next to temp and temp’s next to Null.Hence it becomes a O(N)+O(1)=O(N) operation.
SOURCE CODE:
CODE SNIPPET IS HERECiAgICAgICAgICBOb2RlIGluc2VydEF0RW5kKE5vZGUgaGVhZCwgaW50IHgpCiAgICB7CiAgICAgICAgTm9kZSB0ZW1wPW5ldyBOb2RlKHgpOyAvL2NyZWF0aW5nIGEgdGVtcG9yYXJ5IG5vZGUgd2l0aCBkYXRhIHgKCiAgICAgICAgLyogSWYgaGVhZCBpcyBudWxsICwgdGhlbiBhc3NpZ25pbmcgaGVhZCB0byB0ZW1wKi8KCiAgICAgICAgaWYoaGVhZD09bnVsbCkKICAgICAgICBoZWFkPXRlbXA7CgovKiBFbHNlIGN1cnIgbm9kZSBpcyBhc3NpZ25lZCB0byBoZWFkIGFuZCB3ZSB0cmF2ZXJzZSB0aGUgbGlua2VkbGlzdCB0aWxsIGN1cnJlbnQncyBuZXh0IGlzIG5vdCBudWxsKi8KCiAgICAgICAgTm9kZSBjdXJyPWhlYWQ7CiAgICAgICAgd2hpbGUoY3Vyci5uZXh0IT1udWxsKXsKICAgICAgICAgICAgY3Vycj1jdXJyLm5leHQ7CiAgICAgICAgfQovKk5vdyB3ZSBoYXZlIHRoZSBob2xkIG9mIGxhc3QgZWxlbWVudCBpbiB0aGUgTGlua2VkTGlzdCAsIG5vdyB3ZSBhc3NpZ24gY3VycmVudCdzIG5leHQgdG8gdGVtcCBhbmQgbWFrZSB0ZW1wJ3MgbmV4dCBwb2ludCB0byBudWxsKi8KICAgICAgICAKICAgICAgICBjdXJyLm5leHQ9dGVtcDsKICAgICAgICB0ZW1wLm5leHQ9bnVsbDsKICAgICAgICAKICAgICAgICAvLyByZXR1cm5pbmcgaGVhZCBvZiB0aGUgbGlua2VkbGlzdAogICAgICAgIHJldHVybiBoZWFkOwp9IA==
Q32. What is the time complexity to find the middle node in a Linked List?
The time complexity to find the middle node in a LinkedList is O(N). To find middle node in the linkedlist ,we use two pointer approach.We take two pointers, slow pointer and fast pointer. Initially, both slow pointer and fast pointer are intiailized to head. Then the slow pointer moves one space ahead at a time whereas the fast pointer moves two pointers ahead at time and the traversal continues till fast pointer does not point to null or fast pointer's next does not point to null to keep into mind odd node list as well as even node list.
When either of the cases occur, we print slow.data and that is the middle node of the LinkedList. The algorithm takes care of odd node list as well as even node list . In this case, we are reaching the end of the list by a linear traversal hence it is a O(N) operation.
SOURCE CODE:
CODE SNIPPET IS HEREICBpbnQgZ2V0TWlkZGxlKE5vZGUgaGVhZCkKICAgIHsKICAgICAgICAgTm9kZSBzbG93PWhlYWQsZmFzdD1oZWFkOyAvL2ludGlhbGl6aW5nIHNsb3cgYW5kIGZhc3QgcG9pbnRlcnMgdG8gaGVhZAogICAgICAgICB3aGlsZShmYXN0IT1udWxsJiZmYXN0Lm5leHQhPW51bGwpewogICAgICAgICAgICAgc2xvdz1zbG93Lm5leHQ7IC8vUG9pbnRpbmcgc2xvdyB0byBzbG93Lm5leHQKICAgICAgICAgICAgIGZhc3Q9ZmFzdC5uZXh0Lm5leHQ7Ly9Qb2ludGluZyBmYXN0IHRvIGZhc3QncyBuZXh0ICdzIG5leHQKICAgICAgICAgfQogICAgICAgICByZXR1cm4gc2xvdy5kYXRhOyAvL3JldHVybmluZyBzbG93LmRhdGEKICAgIH0g
Q33. What is the time complexity to delete the middle node in a LinkedList?
The time complexity to delete the middle node in a LinkedList is O(N).
To delete the middle node in the LinkedList,first we need to find the middle of the LinkedList. To find middle node in the linkedlist ,we use two pointer approach.We take two pointers, slow pointer and fast pointer. Initially, both slow pointer and fast pointer are intiailized to head. Then the slow pointer moves one space ahead at a time whereas the fast pointer moves two pointers ahead at time and the traversal continues till fast pointer does not point to null or fast pointer's next does not point to null to keep into mind odd node list as well as even node list.
When either of the cases occur, we print slow.data and that is the middle node of the LinkedList. The algorithm takes care of odd node list as well as even node list . In this case, we are reaching the end of the list by a linear traversal hence it is a O(N) operation.
Now, the middle node’s prev pointer points to middle node’s next which is a O(1) operation. Hence, total of O(N)+O(1)=O(N) operation.
SOURCE CODE:
CODE SNIPPET IS HEREICBOb2RlIGRlbGV0ZU1pZChOb2RlIGhlYWQpIHsKCiAvKklmIGhlYWQgaXMgbnVsbCB3ZSByZXR1cm4gbnVsbCovCiAgICAgICAgIGlmKGhlYWQ9PW51bGwpCiAgICAgICAgICByZXR1cm4gbnVsbDsKCiAgICAgICAgICAvKklmIGhlYWQncyBuZXh0IGlzIG51bGwgdGhlbiB3ZSByZXR1cm4gbnVsbCovCiAgICAgICAgaWYoaGVhZC5uZXh0PT1udWxsKQogICAgICAgICAgICByZXR1cm4gbnVsbDsKCiAgICAvKldlIGtlZXAgb25lIGV4dHJhIHBvaW50ZXIgaW4gYWRkaXRpb24gdG8gc2xvdyBhbmQgZmFzdCBwb2ludGVycyBoZXJlLGkuZS4sIHByZXZpb3VzIHBvaW50ZXIsIHdoaWNoIGtlZXBzIHRoZSB0cmFjayBvZiBwcmV2IGVsZW1lbnQgb2YgdGhlIG1pZGRsZSBlbGVtZW50Ki8gICAgICAgIAoKICAgICAgICBOb2RlIHByZXY9aGVhZDsKICAgICAgICBOb2RlIHNsb3c9aGVhZCxmYXN0PWhlYWQ7CiAgICAgICAgd2hpbGUoZmFzdCE9bnVsbCYmZmFzdC5uZXh0IT1udWxsKXsKICAgICAgICAgICAgcHJldj1zbG93OwogICAgICAgICAgICBzbG93PXNsb3cubmV4dDsKICAgICAgICAgICAgZmFzdD1mYXN0Lm5leHQubmV4dDsKICAgICAgICB9CiAgICAgICBwcmV2Lm5leHQ9c2xvdy5uZXh0OyAvL3BvaW50aW5nIHByZXYncyBuZXh0IHRvIHNsb3cncyBuZXh0CiAgICAgICAgcmV0dXJuIGhlYWQ7IC8vcmV0dXJuaW5nIGhlYWQKICAgIH0g
Q34. What is the time complexity to reverse a Linked List?
The time complexity to reverse a LinkedList is O(N). The time complexity is O(N) because we are running a loop and constantly performing operations which is a O(N) time complexity.
SOURCE CODE:
CODE SNIPPET IS HEREICBOb2RlIHJldmVyc2VMaXN0KE5vZGUgaGVhZCkKICAgIHsKICAgICAgICBOb2RlIGN1cnI9aGVhZCxwcmV2PW51bGw7ICAvL2luaXRpYWxpemluZyBjdXJyIHRvIGhlYWQgYW5kIHByZXYgdG8gbnVsbAoKICAgICAvKiB3aGlsZSBjdXJyIGlzIG5vdCBudWxsIHdlIGRvIHRoZSBmb2xsb3dpbmcgb3BlcmF0aW9uczoKICAgICAgMS4gV2UgYXNzaWduIGN1cnIncyBuZXh0IHRvIG5leHQuCiAgICAgIDIuTWFrZSBjdXJyLm5leHQgcG9pbnQgdG8gcHJldgogICAgICAzLlBvaW50IHByZXYgdG8gY3VycgogICAgICA0LlBvaW50IGN1cnIgdG8gbmV4dCovCgogd2hpbGUoY3VyciE9bnVsbCl7CiAgICAgIE5vZGUgbmV4dD1jdXJyLm5leHQ7CiAgICAgIGN1cnIubmV4dD1wcmV2OwogICAgICBwcmV2PWN1cnI7CiAgICAgIGN1cnI9bmV4dDsKICAgICAgICAgICAgICB9CiAgICAgICAgcmV0dXJuIHByZXY7IC8vcmV0dXJuIHByZXYKICAgICAgICAKICAgICAgICB9IA==
Q35. What is the time complexity to segregate odd and even nodes in a LinkedList?
The time complexity to segregate odd and even nodes in a LinkedList is O(N).To segregate odd and even nodes require a complete traversal of the LinkedList . At each iteration we compare the check the number if it is odd or even and then assign it to the respective pointers. At last , we append the odd’s next to even's head and finally return odd list’s head. So, traversal operation will require O(N) time and each time checking whether it is an odd or an even node will require O(1).So, total time complexity required is O(N)+O(1)=O(N).
SOURCE CODE:
CODE SNIPPET IS HEREICBOb2RlIGRpdmlkZShpbnQgTiwgTm9kZSBoZWFkKXsKICAgICAgICAgICAgICAgIE5vZGUgb2gsIG90OwogICAgICAgIE5vZGUgZWgsIGV0OwogICAgICAgIAogICAgICAgIG9oID0gb3QgPSBlaCA9IGV0ID0gbnVsbDsKICAgICAgICAKICAgICAgICBOb2RlIGN1cnIgPSBoZWFkOwogICAgICAgIAogICAgICAgIHdoaWxlKGN1cnIgIT0gbnVsbCkKICAgICAgICB7CiAgICAgICAgICAgIGlmKGN1cnIuZGF0YSAlIDIgPT0gMCkKICAgICAgICAgICAgewogICAgICAgICAgICAgICAgaWYoZWggPT0gbnVsbCkKICAgICAgICAgICAgICAgICAgICBlaCA9IGN1cnI7CiAgICAgICAgICAgICAgICBlbHNlCiAgICAgICAgICAgICAgICAgICAgZXQubmV4dCA9IGN1cnI7CiAgICAgICAgICAgICAgICBldCA9IGN1cnI7CiAgICAgICAgICAgIH0KICAgICAgICAgICAgZWxzZQogICAgICAgICAgICB7CiAgICAgICAgICAgICAgICBpZihvaCA9PSBudWxsKQogICAgICAgICAgICAgICAgICAgIG9oID0gY3VycjsKICAgICAgICAgICAgICAgIGVsc2UKICAgICAgICAgICAgICAgICAgICBvdC5uZXh0ID0gY3VycjsKICAgICAgICAgICAgICAgIG90ID0gY3VycjsKICAgICAgICAgICAgfQogICAgICAgICAgICAKICAgICAgICAgICAgY3VyciA9IGN1cnIubmV4dDsKICAgICAgICB9CiAgICAgICAgCiAgICAgICAgaWYoZWggPT0gbnVsbCkKICAgICAgICAgICAgcmV0dXJuIG9oOwogICAgICAgIGlmKG9oID09IG51bGwpCiAgICAgICAgICAgIHJldHVybiBlaDsKICAgICAgICAKICAgICAgICBldC5uZXh0ID0gb2g7CiAgICAgICAgb3QubmV4dCA9IG51bGw7CiAgICAgICAgCiAgICAgICAgcmV0dXJuIGVoOwogICAgfSA=
Q36. What is the time complexity to find kth node from end in a LinkedList?
The time complexity to find kth node from end in a LinkedList is O(N). The time complexity is such because we first will need to calculate the total number of nodes and that would involve traversal of the LinkedList which is a O(N) operation. Now, again we need to traverse till the kth node from the end and that is again O(N). Hence, the total time complexity is O(N).
SOURCE CODE:
CODE SNIPPET IS HERECiAgICAgICAgICBpbnQgZ2V0TnRoRnJvbUxhc3QoTm9kZSBoZWFkLCBpbnQgbikKCiAgICB7CgogICAgTm9kZSBjdXJyPWhlYWQ7aW50IGM9MDsKCiAgICBmb3IoY3Vycj1oZWFkO2N1cnIhPW51bGw7Y3Vycj1jdXJyLm5leHQpCgogICAgYysrOwoKICAgIGlmKG4+YykKCiAgICByZXR1cm4gLTE7CgogICAgTm9kZSBzbG93PWhlYWQsZmFzdD1oZWFkOwoKICAgIHdoaWxlKG4tLT4wKQoKICAgIGZhc3Q9ZmFzdC5uZXh0OwoKICAgIHdoaWxlKGZhc3QhPW51bGwpCgogICAgewoKICAgICAgICBzbG93PXNsb3cubmV4dDsKCiAgICAgICAgZmFzdD1mYXN0Lm5leHQ7CgogICAgfQoKICAgIHJldHVybiBzbG93LmRhdGE7CgogICAgfQogICAgICAgIA==
Q37. What is the time complexity to detect loop in a Linked List?
The time complexity to detect loop in a LinkedList is O(N).To find if there is a cycle in the linkedlist ,we use two pointer approach. We take two pointers, slow pointer and fast pointer. Initially, both slow pointer and fast pointer are intiailized to head. Then the slow pointer moves one space ahead at a time whereas the fast pointer moves two pointers ahead at time and the traversal continues till fast pointer does not point to null or fast pointer's next does not point to null.
When either of the cases occur, it means that there is no cycle in the List. But if at some point in the traversal slow and fast become equal, it means that there is a cycle and we return true. It is know as the Floyd's Cycle-Finding Algorithm. So, traversal till either we reach null or find a loop will require a O(N) time.
SOURCE CODE:
CODE SNIPPET IS HERECiAgICAgICAgICBwdWJsaWMgc3RhdGljIGJvb2xlYW4gZGV0ZWN0TG9vcChOb2RlIGhlYWQpewoKTm9kZSBzbG93PWhlYWQsZmFzdD1oZWFkOy8vc2xvdyBhbmQgZmFzdCBwb2ludGVycyBhcmUgaW50aXRpYWxpemVkIHRvIGhlYWQKCi8vV2UgdXNlIHR3byBwb2ludGVyIG1ldGhvZCB0byBkZXRlY3QgbG9vcAoKd2hpbGUoZmFzdCE9bnVsbCYmZmFzdC5uZXh0IT1udWxsKXsKCnNsb3c9c2xvdy5uZXh0OwoKZmFzdD1mYXN0Lm5leHQubmV4dDsKCi8vSWYgc2xvdyBiZWNvbWVzIGVxdWFsIHRvIGZhc3QsIGl0IG1lYW5zIHRoZXJlIGlzIGEgbG9vcCBhbmQgd2UgcmV0dXJuIHRydWUgCgogICAgaWYoc2xvdz09ZmFzdCkKCnJldHVybiB0cnVlOwoKfQoKcmV0dXJuIGZhbHNlOwoKfQogICAgICAgIA==
Q38. What is the time complexity to check if a linked list is palindrome?
The time complexity to check if a LinkedList is palindrome is O(N). To check if a LinkedList is palindrome will require traversal of the LinkedList and then check is it palindrome or not. Hence it is a O(N) operation overall.
SOURCE CODE:
CODE SNIPPET IS HERECiAgICAgICAgICBib29sZWFuIGlzUGFsaW5kcm9tZShOb2RlIGhlYWQpIAogICAgewogICAgICAgIC8vWW91ciBjb2RlIGhlcmUKICAgICAgQXJyYXlEZXF1ZSBzPW5ldyBBcnJheURlcXVlKCk7CiAgICAgICAgZm9yKE5vZGUgY3Vycj1oZWFkO2N1cnIhPW51bGw7Y3Vycj1jdXJyLm5leHQpCiAgICAgICAgcy5wdXNoKGN1cnIuZGF0YSk7CiAgICAgICAgCiAgICAgICAgZm9yKE5vZGUgY3Vycj1oZWFkO2N1cnIhPW51bGw7Y3Vycj1jdXJyLm5leHQpCiAgICAgICAgewogICAgICAgICAgICBpbnQgeD1zLnBvcCgpOwogICAgICAgICAgICBpZih4IT1jdXJyLmRhdGEpCiAgICAgICAgICAgIHJldHVybiBmYWxzZTsKICAgICAgICB9CiAgICAKICAgICAgICByZXR1cm4gdHJ1ZTsKICAgIH0gICAgIA==
Q39. What is the time complexity to find intersection point in Y shaped List?
The time complexity to find intersection point in Y shaped List is O(N). To get the intersection point in the LinkedList, we need to traverse the LinkedLists which are given and each time compare whether the data in both the Lists is same and if it is, then that is the intersection point in the Y-shaped LinkedList. So, traversal requires O(N) and then comparison requires O(1) time making it a linear time operation.
SOURCE CODE:
CODE SNIPPET IS HERECiAgICAgICAgICBpbnQgaW50ZXJzZWN0UG9pbnQoTm9kZSBoZWFkMSwgTm9kZSBoZWFkMikKICAgIHsKICAgICAgICAgaW50IGMxPTAsYzI9MDsKICAgICAgICAgTm9kZSBjdXJyMT1oZWFkMSxjdXJyMj1oZWFkMjsKICAgICAgICAgd2hpbGUoY3VycjEhPW51bGwpewogICAgICAgICAgICAgYzErKzsKICAgICAgICAgICAgIGN1cnIxPWN1cnIxLm5leHQ7CiAgICAgICAgIH0KICAgICAgICAgd2hpbGUoY3VycjIhPW51bGwpewogICAgICAgICAgICAgYzIrKzsKICAgICAgICAgICAgIGN1cnIyPWN1cnIyLm5leHQ7CiAgICAgICAgIH0KICAgICAgICAgaW50IGM9TWF0aC5hYnMoYzEtYzIpOwogICAgICAgICAgY3VycjE9aGVhZDE7Y3VycjI9aGVhZDI7CiAgICAgICAgIGlmKGMxPmMyKXsKICAgICAgICAgICAgIHdoaWxlKGMtLT4wKXsKICAgICAgICAgICAgICAgIGN1cnIxPWN1cnIxLm5leHQ7IAogICAgICAgICAgICAgfQogICAgICAgICB9CiAgICAgICAgIGVsc2V7CiAgICAgICAgICAgICB3aGlsZShjLS0+MCl7CiAgICAgICAgICAgICAgICBjdXJyMj1jdXJyMi5uZXh0OyAKICAgICAgICAgICAgIH0KICAgICAgICAgfQogICAgICAgICB3aGlsZShjdXJyMSE9Y3VycjIpewogICAgICAgICAgICAgY3VycjE9Y3VycjEubmV4dDsKICAgICAgICAgICAgIGN1cnIyPWN1cnIyLm5leHQ7CiAgICAgICAgIH0KICAgICAgICAgcmV0dXJuIGN1cnIxLmRhdGE7Cgp9IA==
Q40. What is the main advantage of Linked List over arrays?
In LinkedList, space is not wasted as preallocation of memory is not done. This is a major advantage of LinkedLists over arrays. Here are some other:
-
An array is a linear collection of data elements and a linked list is a linear collection of nodes.
-
But unlike an array, a linked list does not share its nodes in consecutive memory locations.
-
Another point of difference between an array and a linked list is that a linked list does not allow random access of data.
-
Nodes in a linked list can be accessed only in a sequential manner.
-
Nodes in a linked array, insertions and deletions can be done at any point in the list in a constant time.
-
Another advantage of a linked list over array is that, we can add any number of elements in the list, this is not possible in case of an array.
-
For example, if we declare an array as int a [10], then the array can store maximum of 10 data elements, but not even one more than that, there is no such restriction in case of linked list.
-
Linked list provide an efficient way of storing related data and perform basic operations such as insertion, deletion and updating of information at the cost of extra space required for storing the address.
Q41. What is the time complexity to search an element in a Linked List?
The time complexity to search an element in a LinkedList is O(N).To search an element in the Linked List requires comparison of the element to be searched with the current element.Now, in the worst case it might be possible that the element to be searched is not present in the LinkedList or present in the ending nodes of the LinkedList. So, traversing and comparing each time whether the current node’s data is same as the element that is to be searched takes O(N) time complexity.
SOURCE CODE:
CODE SNIPPET IS HEREICBwdWJsaWMgc3RhdGljIHZvaWQgc2VhcmNoU2luZ2x5TGlua2VkTGlzdChOb2RlIGhlYWQsaW50IHgpewoKICAgIE5vZGUgY3Vycj1oZWFkOyAvL2N1cnJlbnQgbm9kZSBpcyBpbnRpYWxpemVkIHRvIGhlYWQKCiAgICAvKiBpdGVyYXRpbmcgdGlsbCB0aGUgY3VyciB2YWx1ZSBkb2VzIG5vdCBiZWNvbWUgbnVsbCAqLwogICAgd2hpbGUoY3VyciE9bnVsbCkKICAgIHsKCmlmKGN1cnIuZGF0YT09eCkKICAgeyAgU3lzdGVtLm91dC5wcmludGxuKGN1cnIuZGF0YSk7IC8vcHJpbnRpbmcgdGhlIGN1cnIncyBkYXRhIApyZXR1cm47fSAgICAKCmN1cnI9Y3Vyci5uZXh0OwogICAgfQoKU3lzdGVtLm91dC5wcmludGxuKCJFbGVtZW50IE5vdCBGb3VuZCIpOwoKfQogICAgICAgIA==
Q42. Which of the sorting algorithms can be used to sort a random linked list with minimum time complexity?
Merge sort can be used to sort a random linkedlist with minimum time complexity. Mergesort algorithm uses the Divide and Conquer technique and takes O(NlogN) time complexity .
REASON:
The slow random-access performance of a linked list makes other algorithms (such as quicksort) perform poorly, and others (such as heapsort) completely impossible.
Since worst case time complexity of Merge Sort is O(nLogn) and Insertion sort is O(n^2), merge sort is preferred.
Q43. What are the time complexities of finding 8th element from beginning and 8th element from end in a singly linked list? Let n be the number of nodes in linked list, you may assume that n > 8.
The time complexities of finding 8th element from beginning and 8th element from end in a singly linked list are O(1) and O(N) respectively. Since we are at the 8th position accessing the element is a O(1)operation.
But to get the 8th element from the end, we first will need to calculate the total number of nodes and that would involve traversal of the LinkedList which is a O(N) operation. Now, again we need to traverse till the 8th node from the end and that is again O(N). Hence, the total time complexity is O(N).
Searching for an element in a linked list is O(n) operation (worst case), where n is the number of elements in linked list.
So, finding an element that is at 8th position from beginning is O(8) operation, So we can say its O(1) operation. On the other hand finding 8th element from end is equivalent to finding n−8+1 element from beginning. So, its O(n−8+1) operation i.e., O(n) operation.
SOURCE CODE TO GET Kth element from the last:
CODE SNIPPET IS HERECiAgICAgICAgICBpbnQgZ2V0TnRoRnJvbUxhc3QoTm9kZSBoZWFkLCBpbnQgbikKCiAgICB7CgogICAgTm9kZSBjdXJyPWhlYWQ7aW50IGM9MDsKCiAgICBmb3IoY3Vycj1oZWFkO2N1cnIhPW51bGw7Y3Vycj1jdXJyLm5leHQpCgogICAgYysrOwoKICAgIGlmKG4+YykKCiAgICByZXR1cm4gLTE7CgogICAgTm9kZSBzbG93PWhlYWQsZmFzdD1oZWFkOwoKICAgIHdoaWxlKG4tLT4wKQoKICAgIGZhc3Q9ZmFzdC5uZXh0OwoKICAgIHdoaWxlKGZhc3QhPW51bGwpCgogICAgewoKICAgICAgICBzbG93PXNsb3cubmV4dDsKCiAgICAgICAgZmFzdD1mYXN0Lm5leHQ7CgogICAgfQoKICAgIHJldHVybiBzbG93LmRhdGE7CgogICAgfSA=
Q44. Is it possible to create a doubly linked list using only one pointer with every node?
Yes, it is possible to create a doubly linkedlist using only one pointer with every node by storing XOR of addresses of previous and next nodes.
Consider the following linked list:
|0|A|0x01|<->|0x01|B|0x02|<->|0x02|C|0|
The list contains 3 nodes with values A,B,C and prev/next pointer containing hex values(addresses) of the prev/next element in the list. Value 0 is null
Instead of storing 2 pointers, we can use only one, as explained in the article:
|A|0x01|<->|B|0x03|<->|C|0x03|
We'll call the new field link = prev XOR next. So with that in mind:
A.link = 0^0x01 = 0x01
B.link = 0x01^0x02 = 0x03
C.link = 0x03^0x0 = 0x03.
Assuming you have a pointer to the head of the list (which you know has the prev pointer set to null) here's how you iterate through the list:
p=head; prev = 0; while(p.link!=prev) { next = p.link^prev prev=p p=next }
Q45. Given pointer to a node X in a singly linked list. Only one pointer is given, pointer to head node is not given, can we delete the node X from given linked list?
It is possible if X is not last node. Use following two steps:
(a) Copy the data of next of X to X.
(b) Delete next of X.
The following is the function to delete a node with the only pointer given to it:
void deleteNode(Node del) { del.data=del.next.data; del.next=del.next.next; }
Q46. You are given pointers to first and last nodes of a singly linked list, is deleting the last element of the list dependent on the length of the linked list?
Yes , if given pointers to first and last nodes of a singly linked list, deleting the last element of the list dependent on the length of the linked list. Deleting the last element is dependent on the length of the singly linked list because deleting last node would require access to its previous pointer which is a linear time operation and then changing links would further require constant time. Hence, it is the operation which is dependent on the length of the linked list even if first and last nodes’ pointers are given.
Q47. What are the number of comparisons needed to search a singly linked list of length n for a given element in the worst case?
The number of comparisons needed to search a singly linked list of length n for a given element in the worst case are n. To search an element in the Linked List requires comparison of the element to be searched with the current element. Now, in the worst case it might be possible that the element to be searched is not present in the linked list or present in the ending nodes of the LinkedList. So, traversing and comparing each time whether the current node’s data is same as the element that is to be searched takes O(N) time complexity and hence n comparisons in the worst case.
Q48. Suppose each set is represented as a linked list with elements in arbitrary order. Which of the operations among union, intersection, membership, cardinality will be the slowest?
Union and intersection will be the slowest. Union and intersection will require the traversal of the entire linkedlists and then figuring out which will be the intersection and union. So, it will take more operational time. Hence, they both are the slowest operations.
REASON:
For getting intersection of L1 and L2, search for each element of L1 in L2 and print the elements we find in L2.
There can be many ways for getting union of L1 and L2. One of them is as follows
- Print all the nodes of L1 and print only those which are not present in L2.
- Print nodes of L2.
All of these methods will require more operations than intersection as we have to process intersection node plus other nodes.
Q49. Let P be a singly linked list. Let Q be the pointer to an intermediate node x in the list. What is the worst-case time complexity of the best known algorithm to delete the node x from the list?
The worst-case time complexity of the best known algorithm to delete the node x from the list is O(1).The best known algorithm will delete the node in a constant time.
A simple solution is to traverse the linked list until you find the node you want to delete. But this solution requires pointer to the head node which contradicts the problem statement.
Fast solution is to copy the data from the next node to the node to be deleted and delete the next node. Something like following.
CODE SNIPPET IS HERECiAgICAgICAgICAvLyBGaW5kIG5leHQgbm9kZSB1c2luZyBuZXh0IHBvaW50ZXIKICAgIHN0cnVjdCBub2RlICp0ZW1wICA9IG5vZGVfcHRyLT5uZXh0OwoKICAgIC8vIENvcHkgZGF0YSBvZiBuZXh0IG5vZGUgdG8gdGhpcyBub2RlCiAgICBub2RlX3B0ci0+ZGF0YSAgPSB0ZW1wLT5kYXRhOwoKICAgIC8vIFVubGluayBuZXh0IG5vZGUKICAgIG5vZGVfcHRyLT5uZXh0ICA9IHRlbXAtPm5leHQ7CgogICAgLy8gRGVsZXRlIG5leHQgbm9kZQogICAgZnJlZSh0ZW1wKTsKICAgICAgICA=
Time complexity of this approach is O(1).
Q50.The concatenation of two lists is to be performed in O(1) time. Which list should be used?
Circular Doubly LinkedList must be used in the above scenario. Circular Doubly LinkedList will store the data in the fashion where it will have the data, the pointer to previous node, the pointer to next node as well as the last node will be pointing to the first node and the first node’s prev will point to the last node’s next pointer. Hence that will mean that the concatenation of the two lists will require a constant time ,i.e., O(1) time.
Q51. What is a temporary variable in context of linked lists?
A temporary variable is often used as a reference to navigate through the list when performing various operations like traversal, insertion, deletion, and searching. This variable is used to keep track of the current position within the linked list as you move from one node to another.
When you're traversing or modifying a linked list, you typically start from the head node and use a temporary variable to iterate through the list. Here's a common pattern for using a temporary variable in linked list operations:
- Initialize the temporary variable with the head node.
- Use the temporary variable to access the current node's data and perform necessary operations.
- Move the temporary variable to the next node by following the reference (pointer) to the next node.
Q52. Why is binary search not efficient for linked lists?
Binary search is not efficient for linked lists, particularly singly linked lists, because direct access to elements is not as straightforward. For each middle element comparison, one would need to traverse the list from the beginning, which would result in a linear time complexity similar to a linear search. Binary-like search on a linked list would be skip lists or balanced binary search trees (like AVL trees) to maintain a more structured and efficient search pattern.
Q53. What is garbage collection in linked list?
Garbage collection is automatic memory management that handles memory allocation and deallocation. Using this dynamic technique one doesn't need to explicitly manage memory allocation and deallocation like with pointers in languages like C or C++. Garbage collection identifies dead memory blocks and reallocates storage for reuse.
With this we come to the end of the article. As discussed, studying LinkedList is important for interviews. These advanced questions on linked list will brush up your knowledge and prepare you well for dream job interview. All the best!
You may also like to read:
As a biotechnologist-turned-writer, I love turning complex ideas into meaningful stories that inform and inspire. Outside of writing, I enjoy cooking, reading, and travelling, each giving me fresh perspectives and inspiration for my work.
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter
Blogs you need to hog!

This Is My First Hackathon, How Should I Prepare? (Tips & Hackathon Questions Inside)

10 Best C++ IDEs That Developers Mention The Most!

Advantages and Disadvantages of Cloud Computing That You Should Know!









Comments
Add comment