Dynamic Programming - From Basics To Advanced (+Code Examples)

0 min read

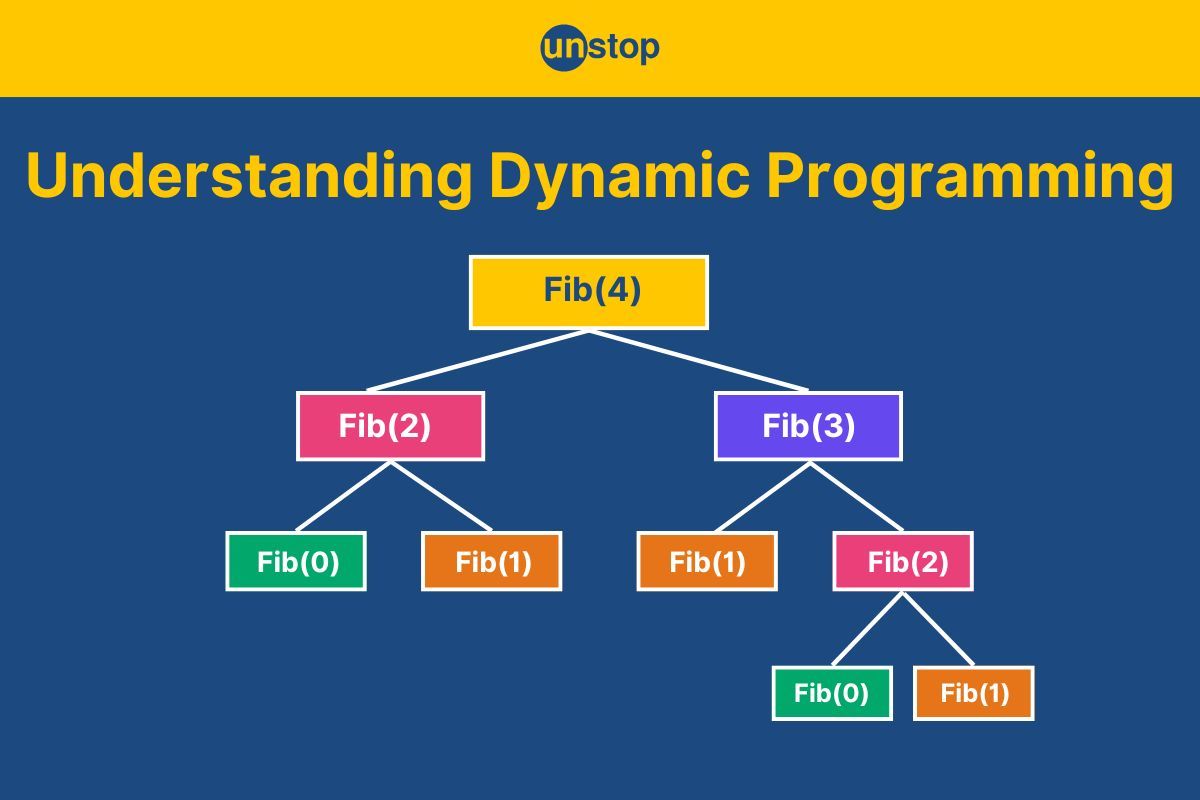
Dynamic Programming (DP) is a technique for solving problems by breaking them into smaller, overlapping subproblems and reusing solutions to save time. It is ideal for optimization and recursive problems, ensuring efficiency by avoiding redundant computations. 

In this article, we will explore the core concepts of dynamic programming and its key principles and provide step-by-step guides with real-world examples.

What Is Dynamic Programming?

Dynamic programming (DP) is a problem-solving approach used in computer science to solve problems by breaking them into smaller overlapping subproblems. It is particularly effective for optimization problems and those with a recursive structure.

Key Concepts Of Dynamic Programming:

1. Optimal Substructure: A problem exhibits optimal substructure if its solution can be constructed efficiently from the solutions of its smaller subproblems.
• Example: Finding the shortest path in a graph involves combining the shortest paths of smaller subgraphs.
2. Overlapping Subproblems: Many problems involve solving the same subproblem multiple times. DP solves each subproblem once and stores the results to avoid redundant computations.
• Example: Fibonacci numbers – calculating F(n) involves repeated calculations of F(n-1) and F(n-2).
3. Memoization (Top-Down Approach): In this approach, results of subproblems are stored in a data structure (like a dictionary or array) during recursion to avoid recalculating them.
• Example: Recursive Fibonacci with memoization.
4. Tabulation (Bottom-Up Approach): In this approach, subproblems are solved iteratively, and the results are stored in a table (usually an array) to build up the solution for the larger problem.
• Example: Iterative Fibonacci using an array.

Real-Life Example: The Jigsaw Puzzle Analogy

Dynamic programming can be understood with the analogy of solving a jigsaw puzzle efficiently. Imagine you are solving a large jigsaw puzzle. Instead of trying random pieces to see what fits (brute force), you use a systematic approach:

1. Break It Down:
   You group the puzzle pieces by color or pattern (e.g., edges, sky, trees, etc.), making it easier to focus on smaller parts of the puzzle.
2. Reuse Your Work:
   Once you solve a smaller section (e.g., the sky), you don’t revisit it or redo it. Instead, you place it aside, knowing it’s solved. This is like memoization in dynamic programming.
3. Build Step by Step:
   After solving smaller sections, you combine them to form larger sections (e.g., attaching the sky to the trees). This is similar to tabulation, where you solve subproblems iteratively and build up to the final solution.
4. Avoid Redundancy:
   If you’ve already figured out where a piece fits, you don’t test it again in other places. This prevents repetitive work and saves time.

How This Relates To Dynamic Programming:

• Grouping puzzle pieces: Breaking the problem into subproblems.
• Saving smaller sections: Storing solutions of subproblems to avoid redundant work.
• Combining sections: Using smaller solutions to build the final answer.
• Avoiding redundancy: Ensuring each subproblem is solved only once.

Dynamic programming, like solving a puzzle this way, is all about organization, reuse, and efficiency.

How To Solve A Problem Using Dynamic Programming?

Solving a problem using dynamic programming (DP) involves following a structured approach. Here's a step-by-step guide:

Steps to Solve a Problem Using Dynamic Programming:

1. Understand the Problem Clearly
• Read the problem statement carefully.
• Identify what needs to be optimized or calculated.
2. Check for DP Characteristics
• Optimal Substructure: Can the problem be broken into smaller, simpler subproblems?
• Overlapping Subproblems: Are some subproblems solved multiple times in a naive solution?
3. Define the State
• Decide on the variables that represent the subproblem.
• For example, in the Fibonacci problem, the state can be F(n) representing the nth Fibonacci number.
4. Formulate the Recurrence Relation
• Write a mathematical relation that connects the solution of the current subproblem to smaller subproblems.
• Example for Fibonacci: F(n)=F(n−1)+F(n−2)
5. Choose an Approach
• Memoization (Top-Down): Solve the problem recursively and store results to avoid recomputation.
• Tabulation (Bottom-Up): Solve subproblems iteratively, starting from the smallest and building up to the final solution.
6. Define Base Cases
• Establish the solutions for the simplest subproblems, which will act as starting points.
• Example for Fibonacci: F(0)=0, F(1)=1
7. Implement the Solution
• Write code using your chosen approach.
• Use appropriate data structures (e.g., arrays, lists, or dictionaries) to store intermediate results.
8. Optimize Space (if needed)
• If only a few previous states are required, reduce space usage by storing only those.
• Example: In Fibonacci, reduce space complexity from O(n) to O(1).
9. Test the Solution Thoroughly
• Validate the implementation using various test cases, including edge cases.
• Example: For Fibonacci, test with n=0,1,10,50, etc.

Dynamic Programming Algorithm Techniques

Dynamic programming (DP) involves solving complex problems by breaking them into overlapping subproblems. The two main techniques are:

1. Memoization (Top-Down Approach)

Memoization is a top-down technique where recursive calls store results of subproblems in a cache to avoid redundant calculations.

Concept:

• Solve the problem recursively.
• Store the results of already solved subproblems in a cache (e.g., dictionary or array).
• When the same subproblem arises again, retrieve the result from the cache instead of recomputing it.

Key Characteristics:

• Recursive in nature.
• Saves computation time by avoiding redundant calculations.
• Can be slower for problems with deep recursion due to function call overhead.

Code Example: Fibonacci Using Memoization

ZGVmIGZpYm9uYWNjaV9tZW1vaXphdGlvbihuLCBtZW1vPXt9KToKICAgICMgQ2hlY2sgaWYgcmVzdWx0IGlzIGFscmVhZHkgY29tcHV0ZWQKICAgIGlmIG4gaW4gbWVtbzoKICAgICAgICByZXR1cm4gbWVtb1tuXQogICAgCiAgICAjIEJhc2UgY2FzZXMKICAgIGlmIG4gPT0gMDogCiAgICAgICAgcmV0dXJuIDAKICAgIGlmIG4gPT0gMTogCiAgICAgICAgcmV0dXJuIDEKICAgIAogICAgIyBSZWN1cnNpdmVseSBjYWxjdWxhdGUgYW5kIHN0b3JlIHRoZSByZXN1bHQgaW4gbWVtbwogICAgbWVtb1tuXSA9IGZpYm9uYWNjaV9tZW1vaXphdGlvbihuIC0gMSwgbWVtbykgKyBmaWJvbmFjY2lfbWVtb2l6YXRpb24obiAtIDIsIG1lbW8pCiAgICByZXR1cm4gbWVtb1tuXQoKIyBFeGFtcGxlIHVzYWdlCm4gPSAxMApwcmludCgiRmlib25hY2NpIG51bWJlciBhdCBwb3NpdGlvbiIsIG4sICI6IiwgZmlib25hY2NpX21lbW9pemF0aW9uKG4pKQo=

Output: 

Fibonacci number at position 10 : 55

Explanation: 

In the above code example-

1. We start with a function fibonacci_memoization that computes Fibonacci numbers using a technique called memoization, which helps us avoid redundant calculations.
2. The function takes two parameters: n (the position in the Fibonacci sequence) and an optional dictionary memo to store previously computed results.
3. We first check if the result for the current n is already in memo. If it is, we directly return it, saving computational effort.
4. For the base cases: if n is 0, we return 0; if n is 1, we return 1. These are the starting points of the Fibonacci sequence.
5. If the result is not already computed, we calculate it recursively by summing the results of fibonacci_memoization(n - 1, memo) and fibonacci_memoization(n - 2, memo).
6. After calculating the value, we store it in memo to avoid recomputing it in future calls.
7. Finally, we return the computed value.
8. When we call fibonacci_memoization(10), the function computes the 10th Fibonacci number. By using memoization, we ensure that intermediate results are reused efficiently, making the function much faster than naive recursion.

2. Tabulation (Bottom-Up Approach)

Tabulation is a bottom-up technique where the solution to a problem is built iteratively from the smallest subproblems up to the main problem, using a table to store intermediate results.

Concept:

• Solve the problem iteratively from the smallest subproblems up to the main problem.
• Use a table (e.g., array) to store results for subproblems.
• Each subproblem builds on the results of previously solved subproblems.

Key Characteristics:

• Iterative in nature.
• Avoids recursion and function call overhead.
• Often uses less space compared to memoization (no recursion stack).

Code Example: Fibonacci Using Tabulation

ZGVmIGZpYm9uYWNjaV90YWJ1bGF0aW9uKG4pOgogICAgIyBIYW5kbGUgYmFzZSBjYXNlcwogICAgaWYgbiA9PSAwOiAKICAgICAgICByZXR1cm4gMAogICAgaWYgbiA9PSAxOiAKICAgICAgICByZXR1cm4gMQogICAgCiAgICAjIENyZWF0ZSBhIHRhYmxlIHRvIHN0b3JlIEZpYm9uYWNjaSB2YWx1ZXMKICAgIGRwID0gWzBdICogKG4gKyAxKQogICAgZHBbMF0sIGRwWzFdID0gMCwgMSAgIyBCYXNlIGNhc2VzCiAgICAKICAgICMgRmlsbCB0aGUgdGFibGUgaXRlcmF0aXZlbHkKICAgIGZvciBpIGluIHJhbmdlKDIsIG4gKyAxKToKICAgICAgICBkcFtpXSA9IGRwW2kgLSAxXSArIGRwW2kgLSAyXQogICAgCiAgICByZXR1cm4gZHBbbl0KCiMgRXhhbXBsZSB1c2FnZQpuID0gMTAKcHJpbnQoIkZpYm9uYWNjaSBudW1iZXIgYXQgcG9zaXRpb24iLCBuLCAiOiIsIGZpYm9uYWNjaV90YWJ1bGF0aW9uKG4pKQo=

Output: 

Fibonacci number at position 10 : 55

Explanation: 

In the above code example-

1. We define a function fibonacci_tabulation to compute Fibonacci numbers using tabulation, which involves building a table (array) to store intermediate results.
2. The function takes one parameter n, the position in the Fibonacci sequence.
3. We first handle the base cases: if n is 0, we return 0, and if n is 1, we return 1. These are the starting points of the sequence.
4. We then create a list dp of size n + 1 initialized with zeros. This list will store the Fibonacci values at each position.
5. We set dp[0] to 0 and dp[1] to 1, as they represent the base cases.
6. Next, we use a loop starting from index 2 to n to fill the table. At each step, we calculate dp[i] as the sum of dp[i - 1] and dp[i - 2]. This ensures that each Fibonacci number is calculated based on the two previous numbers.
7. After completing the loop, we return dp[n], which holds the Fibonacci number at position n.
8. When we call fibonacci_tabulation(10), the function calculates the 10th Fibonacci number by filling up the table iteratively, avoiding recursion and making the process more efficient.

Comparison Of Memoization And Tabulation:

Advantages Of Dynamic Programming

Some of the common advantages of dynamic programming algorithm are: 

1. Optimal Substructure: DP ensures that a problem can be broken down into simpler subproblems, and solutions to those subproblems are combined to solve the overall problem optimally.
2. Avoids Redundant Calculations: By storing the results of previously solved subproblems (either in a table or cache), DP significantly reduces the computation time, especially in problems with overlapping subproblems.
3. Improves Efficiency: With DP, problems that would otherwise take exponential time (like the Fibonacci sequence or the knapsack problem) can be solved in polynomial time.
4. Provides Clear Structure: The recursive structure of the problem and the defined relationship between subproblems make DP easy to model and understand once the recurrence relation is identified.

Disadvantages Of Dynamic Programming

Some of the common disadvantages of dynamic programming are: 

1. Space Complexity: DP requires additional memory to store the intermediate results, which can sometimes be prohibitive, especially in problems with a large number of subproblems.
2. Overhead: The need to store and retrieve intermediate results (in memoization) or iterate over large tables (in tabulation) can introduce overhead, especially in problems where the number of subproblems is very large.
3. Complex Implementation: Identifying the optimal substructure, formulating the recurrence relation, and setting up the state and transition can sometimes be difficult, especially for complex problems.
4. Not Always Applicable: Not all problems exhibit optimal substructure and overlapping subproblems, making DP unsuitable for many types of problems.

Applications Of Dynamic Programming 

Some of the important applications of dynamic programming are: 

1. Fibonacci Numbers: Classic example where DP reduces the exponential time complexity of the recursive approach to linear time.
2. Knapsack Problem: DP is widely used to solve optimization problems, like the knapsack problem, where we need to maximize or minimize a certain quantity (e.g., profit or cost) while adhering to constraints.
3. Longest Common Subsequence (LCS): In string matching problems, DP helps in finding the longest common subsequence between two strings, commonly used in bioinformatics and text comparison.
4. Matrix Chain Multiplication: DP is used in problems where the goal is to optimize the order of matrix multiplication to minimize computational cost.
5. Shortest Path Problems (e.g., Floyd-Warshall, Bellman-Ford): DP is used to find the shortest paths between vertices in a graph, which is useful in routing algorithms, network optimization, and GPS navigation.
6. Edit Distance (Levenshtein Distance): DP helps in calculating the minimum number of operations (insertions, deletions, substitutions) required to convert one string into another, commonly used in spell checkers and text comparison.
7. Game Theory: DP can be used to optimize decision-making strategies in games, such as minimizing or maximizing a player's advantage.
8. Resource Allocation Problems: In resource scheduling, job scheduling, or project management, DP can optimize allocation to minimize time, cost, or other factors.

Conclusion

Dynamic Programming (DP) is an essential technique for solving complex problems that involve optimization and can be broken down into simpler overlapping subproblems. By leveraging memoization (top-down) or tabulation (bottom-up), DP optimizes the computation process, drastically reducing time complexity and avoiding redundant calculations. However, it is important to note that DP is most effective when the problem exhibits optimal substructure and overlapping subproblems. 

While DP offers numerous advantages, such as efficiency and clarity, it can come with challenges like increased space complexity and implementation complexity. Despite these drawbacks, DP remains a powerful tool widely applied in areas such as optimization, pathfinding, string matching, and game theory. Understanding when and how to apply DP can help solve problems that would otherwise be intractable with brute-force approaches.

Frequently Asked Questions

Q. What is Dynamic Programming?

Dynamic Programming algorithm(DP) is a problem-solving technique used to solve optimization problems by breaking them down into smaller overlapping subproblems. DP stores the results of these subproblems to avoid redundant calculations, improving time complexity. It is typically used when a problem has optimal substructure and overlapping subproblems, making it suitable for problems like the Fibonacci sequence, knapsack problem, and shortest path problems.

Q. What are the two main techniques used in Dynamic Programming?

The two main techniques in Dynamic Programming are:

• Memoization (Top-Down): This technique uses recursion to solve subproblems and stores the results in a cache (usually a dictionary or array). It avoids recalculating the same subproblem by checking if the result is already stored.
• Tabulation (Bottom-Up): This technique builds the solution iteratively, starting from the smallest subproblem and solving progressively larger problems. It uses a table to store the results of subproblems.

Q. What is the difference between Memoization and Tabulation?

• Memoization is a top-down approach that uses recursion and caches the results of subproblems, reducing redundant calculations.
• Tabulation is a bottom-up approach where we iteratively solve subproblems in increasing order of size, filling a table to store intermediate results.

The primary difference lies in the way the problem is approached: memoization relies on recursion and is typically easier to implement for complex problems, while tabulation is more iterative and may have less memory overhead due to the lack of recursion.

Q. What are the key characteristics of a problem that make Dynamic Programming applicable?

Dynamic Programming is applicable to problems that exhibit the following two key characteristics:

• Optimal Substructure: The problem can be broken down into smaller subproblems that can be solved independently and combined to form the solution.
• Overlapping Subproblems: The problem contains many instances of the same subproblems, which can be solved once and stored for future use, thus avoiding redundant computations.

Q. What are the main advantages of using Dynamic Programming?

The main advantages of Dynamic Programming include:

• Efficiency: DP reduces time complexity by avoiding redundant calculations through caching or tabulating subproblem results.
• Optimal Solutions: DP guarantees finding the optimal solution to problems by systematically evaluating all possibilities.
• Improved Time Complexity: For problems with overlapping subproblems, DP can reduce exponential time complexity to polynomial time, making complex problems solvable in a reasonable amount of time.

You may also like to read: 

1. Difference Between Hashing And Encryption Decoded
2. 53 Frequently Asked Linked List Interview Questions With Answers 2024
3. Data Structure Interview Questions For 2024 [With Detailed Answers]
4. Tree Topology | Advantages & Disadvantages In Computer Network
5. Decoding Data Redundancy In DBMS| Causes, Advantages, Solutions