- What Is Data Structure?
- Key Features Of Data Structures
- Basic Terminologies Related To Data Structures
- Types Of Data Structures
- What Are Linear Data Structures & Its Types?
- What Are Non-Linear Data Structures & Its Types?
- Importance Of Data Structure In Programming
- Basic Operations On Data Structures
- Applications Of Data Structures
- Real-Life Applications Of Data Structures
- Linear Vs. Non-linear Data Structures
- What Are Algorithms? The Difference Between Data Structures & Algorithms
- Conclusion
- Frequently Asked Questions
- What Is Asymptotic Notation?
- How Asymptotic Notation Helps In Analyzing Performance
- Types Of Asymptotic Notation
- Big-O Notation (O)
- Omega Notation (Ω)
- Theta Notation (Θ)
- Little-O Notation (o)
- Little-Omega Notation (ω)
- Summary Of Asymptotic Notations
- Real-World Applications Of Asymptotic Notation
- Conclusion
- Frequently Asked Questions
- Understanding Big O Notation
- Types Of Time Complexity
- Space Complexity In Big O Notation
- How To Determine Big O Complexity
- Best, Worst, And Average Case Complexity
- Applications Of Big O Notation
- Conclusion
- Frequently Asked Questions
- What Is Time Complexity?
- Why Do You Need To Calculate Time Complexity?
- The Time Complexity Algorithm Cases
- Time Complexity: Different Types Of Asymptotic Notations
- How To Calculate Time Complexity?
- Time Complexity Of Sorting Algorithms
- Time Complexity Of Searching Algorithms
- Writing And optimizing An algorithm
- What Is Space Complexity And Its Significance?
- Relation Between Time And Space Complexity
- Conclusion
- What Is Linear Data Structure?
- Key Characteristics Of Linear Data Structures
- What Are The Types Of Linear Data Structures?
- What Is An Array Linear Data Structure?
- What Are Linked Lists Linear Data Structure?
- What Is A Stack Linear Data Structure?
- What Is A Queue Linear Data Structure?
- Most Common Operations Performed in Linear Data Structures
- Advantages Of Linear Data Structures
- What Is Nonlinear Data Structure?
- Difference Between Linear & Non-Linear Data Structures
- Who Uses Linear Data Structures?
- Conclusion
- Frequently Asked Questions
- What is a linear data structure?
- What is a non-linear data structure?
- Difference between linear data structure and non-linear data structure
- FAQs about linear and non-linear data structures
- What Is Search?
- What Is Linear Search In Data Structure?
- What Is Linear Search Algorithm?
- Working Of Linear Search Algorithm
- Complexity Of Linear Search Algorithm In Data Structures
- Implementations Of Linear Search Algorithm In Different Programming Languages
- Real-World Applications Of Linear Search In Data Structure
- Advantages & Disadvantages Of Linear Search
- Best Practices For Using Linear Search Algorithm
- Conclusion
- Frequently Asked Questions
- What Is The Binary Search Algorithm?
- Conditions For Using Binary Search
- Steps For Implementing Binary Search
- Iterative Method For Binary Search With Implementation Examples
- Recursive Method For Binary Search
- Complexity Analysis Of Binary Search Algorithm
- Iterative Vs. Recursive Implementation Of Binary Search
- Advantages & Disadvantages Of Binary Search
- Practical Applications & Real-World Examples Of Binary Search
- Conclusion
- Frequently Asked Questions
- Understanding The Jump Search Algorithm
- How Jump Search Works?
- Code Implementation Of Jump Search Algorithm
- Time And Space Complexity Analysis
- Advantages Of Jump Search
- Disadvantages Of Jump Search
- Applications Of Jump Search
- Conclusion
- Frequently Asked Questions
- What Is Sorting In Data Structures?
- What Is Bubble Sort?
- What Is Selection Sort?
- What Is Insertion Sort?
- What Is Merge Sort?
- What Is Quick Sort?
- What Is Heap Sort?
- What Is Radix Sort?
- What Is Bucket Sort?
- What Is Counting Sort?
- What Is Shell Sort?
- Choosing The Right Sorting Algorithm
- Applications Of Sorting
- Conclusion
- Frequently Asked Questions
- Understanding Bubble Sort Algorithm
- Bubble Sort Algorithm
- Implementation Of Bubble Sort In C++
- Time And Space Complexity Analysis Of Bubble Sort Algorithm
- Advantages Of Bubble Sort Algorithm
- Disadvantages Of Bubble Sort Algorithm
- Applications of Bubble Sort Algorithms
- Conclusion
- Frequently Asked Questions
- Understanding The Merge Sort Algorithm
- Algorithm For Merge Sort
- Implementation Of Merge Sort In C++
- Time And Space Complexity Analysis Of Merge Sort
- Advantages And Disadvantages Of Merge Sort
- Applications Of Merge Sort
- Conclusion
- Frequently Asked Questions
- Understanding The Selection Sort Algorithm
- Algorithmic Approach To Selection Sort
- Implementation Of Selection Sort Algorithm
- Complexity Analysis Of Selection Sort
- Comparison Of Selection Sort With Other Sorting Algorithms
- Advantages And Disadvantages Of Selection Sort
- Application Of Selection Sort
- Conclusion
- Frequently Asked Questions
- What Is Insertion Sort Algorithm?
- How Does Insertion Sort Work? (Step-by-Step Explanation)
- Implementation of Insertion Sort in C++
- Time And Space Complexity Of Insertion Sort
- Applications Of Insertion Sort Algorithm
- Comparison With Other Sorting Algorithms
- Conclusion
- Frequently Asked Questions
- Understanding Quick Sort Algorithm
- Step-By-Step Working Of Quick Sort
- Implementation Of Quick Sort Algorithm
- Time Complexity Analysis Of Quick Sort
- Advantages Of Quick Sort Algorithm
- Disadvantages Of Quick Sort Algorithm
- Applications Of Quick Sort Algorithm
- Conclusion
- Frequently Asked Questions
- Understanding The Heap Data Structure
- Working Of Heap Sort Algorithm
- Implementation Of Heap Sort Algorithm
- Advantages Of Heap Sort
- Disadvantages Of Heap Sort
- Real-World Applications Of Heap Sort
- Conclusion
- Frequently Asked Questions
- Understanding The Counting Sort Algorithm
- Conditions For Using Counting Sort Algorithm
- How Counting Sort Algorithm Works?
- Implementation Of Counting Sort Algorithm
- Time And Space Complexity Analysis Of Counting Sort
- Comparison Of Counting Sort With Other Sorting Algorithms
- Advantages Of Counting Sort Algorithm
- Disadvantages Of Counting Sort Algorithm
- Applications Of Counting Sort Algorithm
- Conclusion
- Frequently Asked Questions
- Understanding Shell Sort Algorithm
- Working Of Shell Sort Algorithm
- Implementation Of Shell Sort Algorithm
- Time Complexity Analysis Of Shell Sort Algorithm
- Advantages Of Shell Sort Algorithm
- Disadvantages Of Shell Sort Algorithm
- Applications Of Shell Sort Algorithm
- Conclusion
- Frequently Asked Questions
- What Is Linked List In Data Structures?
- Types Of Linked Lists In Data Structures
- Linked List Operations In Data Structures
- Advantages And Disadvantages Of Linked Lists In Data Structures
- Comparison Of Linked Lists And Arrays
- Applications Of Linked Lists
- Conclusion
- Frequently Asked Questions
- What Is A Singly Linked List In Data Structure?
- Insertion Operations On Singly Linked Lists
- Deletion Operation On Singly Linked List
- Searching For Elements In Single Linked List
- Calculating Length Of Single Linked List
- Practical Applications Of Singly Linked Lists In Data Structure
- Common Problems With Singly Linked Lists
- Conclusion
- Frequently Asked Questions (FAQ)
- What Is A Linked List?
- Reverse A Linked List
- How To Reverse A Linked List? (Approaches)
- Recursive Approach To Reverse A Linked List
- Iterative Approach To Reverse A Linked List
- Using Stack To Reverse A Linked List
- Complexity Analysis Of Different Approaches To Reverse A Linked List
- Conclusion
- Frequently Asked Questions
- What Is A Stack In Data Structure?
- Understanding Stack Operations
- Stack Implementation In Data Structures
- Stack Implementation Using Arrays
- Stack Implementation Using Linked Lists
- Comparison: Array vs. Linked List Implementation
- Applications Of Stack In Data Structures
- Advantages And Disadvantages Of Stack Data Structure
- Conclusion
- Frequently Asked Questions
- What Is A Graph Data Structure?
- Importance Of Graph Data Structures
- Types Of Graphs In Data Structure
- Types Of Graph Algorithms
- Application Of Graphs In Data Structures
- Challenges And Complexities In Graphs
- Conclusion
- Frequently Asked Questions
- What Is Tree Data Structure?
- Terminologies Of Tree Data Structure:
- Different Types Of Tree Data Structures
- Basic Operations On Tree Data Structure
- Applications Of Tree Data Structures
- Comparison Of Trees, Graphs, And Linear Data Structures
- Advantages Of Tree Data Structure
- Disadvantages Of Tree Data Structure
- Conclusion
- Frequently Asked Questions
- What Is Dynamic Programming?
- Real-Life Example: The Jigsaw Puzzle Analogy
- How To Solve A Problem Using Dynamic Programming?
- Dynamic Programming Algorithm Techniques
- Advantages Of Dynamic Programming
- Disadvantages Of Dynamic Programming
- Applications Of Dynamic Programming
- Conclusion
- Frequently Asked Questions
- Understanding The Sliding Window Algorithm
- How Does The Sliding Window Algorithm Works?
- How To Identify Sliding Window Problems?
- Fixed-Size Sliding Window Example: Maximum Sum Subarray Of Size k
- Variable-Size Sliding Window Example: Smallest Subarray With A Given Sum
- Advantages Of Sliding Window Technique
- Disadvantages Of Sliding Window Technique
- Conclusion
- Frequently Asked Questions
- Introduction To Data Structures
- Data Structures Interview Questions: Basics
- Data Structures Interview Questions: Intermediate
- Data Structures Interview Questions: Advanced
- Conclusion
55+ Data Structure Interview Questions For 2026 (Detailed Answers)

Having a strong grasp of data structures is crucial when preparing for a technical interview. In this article, we will cover a range of important data structures interview questions designed to test your understanding and ability to apply these concepts in real-world scenarios. Whether you're an experienced professional or just starting your career, these data structures and algorithms interview questions will help you prepare for your next interview and sharpen your skills.
Introduction To Data Structures
Data structures are fundamental concepts in computer science, serving as the backbone for organizing and managing data. They provide a way to handle large amounts of data and perform operations like searching, sorting, and modifying it efficiently. Let’s look at some of the most commonly used data structures:
| Data Structure | Definition |
|---|---|
| Array | A collection of elements of the same type stored in contiguous memory locations. |
| Structure (struct) | A custom data type that groups variables of different types under a single name. |
| Union | A special data type that allows storing different structured data types in the same memory location. |
| Linked List | A collection of nodes where each node contains data and a pointer to the next node. |
| Stack | A linear data structure following the Last In, First Out (LIFO) principle. |
| Queue | A linear data structure following the First In, First Out (FIFO) principle. |
| Tree | A hierarchical data structure with nodes connected by edges, with one root node. |
| Graph | A collection of nodes (vertices) connected by edges, used to represent relationships. |
| Hash Table | A data structure that maps keys to values using a hash function for fast access. |
| File | An abstraction for reading from and writing to external storage like hard drives. |
Now that we have a basic understanding of data structures and their fundamental concepts let's explore some of the most commonly asked data structures and algorithm (DSA) interview questions with answers. We have classified these questions into three main categories:
1. Basic Level Data Structures Interview Questions
2. Intermediate Level Data Structures Interview Questions
3. Advanced Level Data Structures Interview Questions
Let's look at each of these sections in detail.

Data Structures Interview Questions: Basics
1. What is a data structure? Explain its key aspects.
A data structure is a way of organizing and storing data to be accessed and modified efficiently. It defines the layout of data, the relationships among data elements, and the operations that can be performed on them.
Key Aspects of Data Structures:
-
Organization: Data structures determine how data is organized and how different data elements are related to each other. This organization can affect the efficiency of data manipulation and retrieval.
-
Storage: They specify how data is stored in memory, whether it is in a contiguous block (as in arrays) or distributed across memory (as in linked lists).
-
Operations: Data structures define the operations that can be performed on the data, such as insertion, deletion, traversal, searching, and sorting. The efficiency of these operations often depends on the choice of data structure.
-
Type of Data: Different data structures are optimized for different types of data and operations. For example, arrays and lists are suitable for sequential data, while trees and graphs are used for hierarchical and networked data.
2. Differentiate between linear and non-linear data structures. Provide examples of each.
Here's a table that lists the key differences between linear and non-linear data structures:
| Aspect | Linear Data Structures | Non-Linear Data Structures |
|---|---|---|
| Definition | Data structures where elements are arranged sequentially, with each element connected to its previous and next elements. | Data structures where elements are arranged hierarchically, and elements can have multiple relationships. |
| Traversal | Traversal is done in a single level, usually in a straight line, from one element to the next. | Traversal can be done on multiple levels and may require visiting multiple branches. |
| Memory Utilization | Memory utilization is generally contiguous (e.g., arrays) but can also be non-contiguous (e.g., linked lists). | Memory utilization is non-contiguous due to its hierarchical nature. |
| Complexity | Simpler in structure and implementation. | More complex in structure and implementation due to hierarchical relationships. |
| Examples | Array, Linked List, Stack, Queue | Tree (Binary Tree, AVL Tree, etc.), Graph (Directed, Undirected) |
| Access Time | Generally faster due to sequential access. | Can be slower due to multiple paths and hierarchical access. |
| Applications | Used for simple data storage and access, like in queues for task scheduling. | Used for more complex relationships, like organizational structures, networks, and databases. |
3. What is a binary tree?
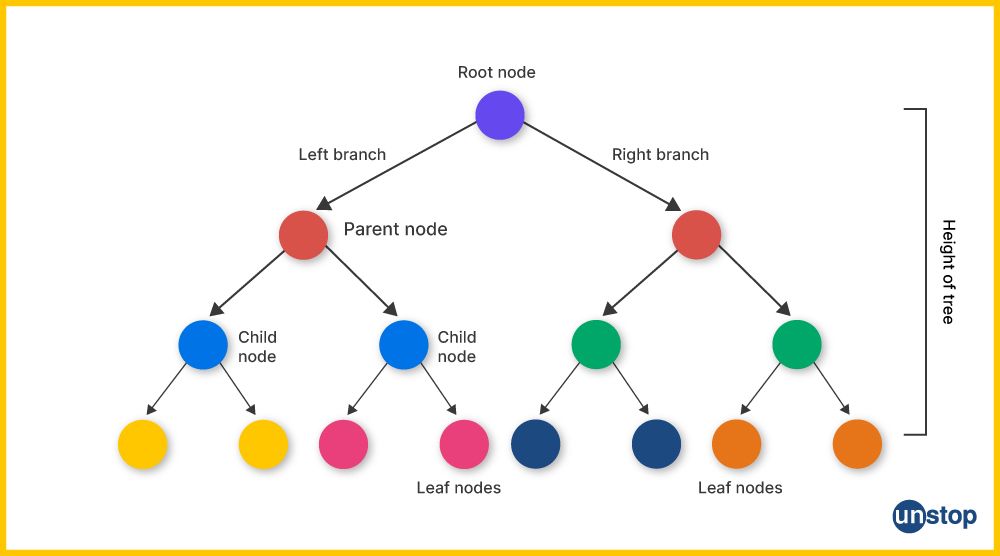
A binary tree is a type of non-linear data structure in which each node has at most two children, referred to as the left child and the right child. The structure is hierarchical, with a single node known as the root at the top, and each subsequent node connecting to its child nodes.
Key characteristics of a binary tree include:
- Root Node: The topmost node in the tree.
- Leaf Nodes: Nodes that do not have any children.
- Internal Nodes: Nodes with at least one child.
- Subtree: A smaller tree within the larger binary tree, starting from any node and including all its descendants.
4. What are dynamic data structures in programming?
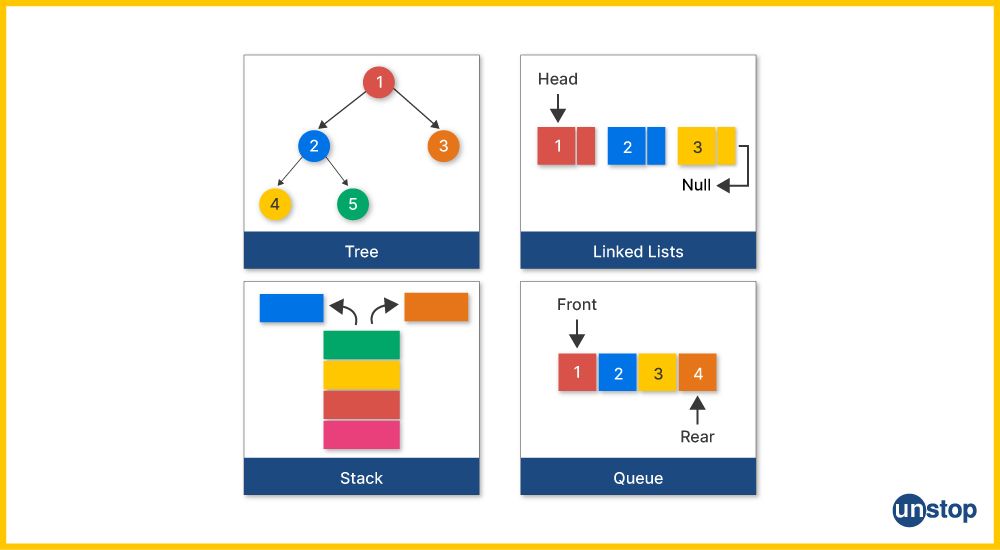
Dynamic data structures are types of data structures that can grow and shrink in size during program execution. Unlike static data structures (like arrays), which have a fixed size determined at compile time, dynamic data structures can adapt to the changing needs of a program
-
Linked Lists: Consists of nodes where each root node contains data and a reference (or link) to the next node. This allows for efficient insertion and deletion of elements.
-
Stacks: Follow the Last In, First Out (LIFO) principle. Elements are added and removed from the top of the stack. They are often implemented using linked lists.
-
Queues: Follow the First In, First Out (FIFO) principle. Elements are added to the back and removed from the front. They can also be implemented with linked lists.
-
Trees: Hierarchical structures where each node has zero or more child nodes. Common types include binary trees, AVL trees, and red-black trees.
-
Hash Tables: Store key-value pairs and use a hash function to quickly access elements based on their keys.
5. What is a linked list? Explain its types.
A linked list is a linear data structure in which elements are stored in nodes, and each node points to the next node in the sequence. Unlike data structures like arrays, linked lists do not require contiguous memory allocation; instead, each node contains a reference (or pointer) to the next node, creating a chain-like structure.
Types of linked lists:
- Singly Linked List: Each node has a single pointer to the next node, allowing traversal in one direction.
- Doubly Linked List: Each node has two pointers: one to the next node and one to the previous node, allowing traversal in both directions.
- Circular Linked List: The last node points back to the head node, forming a circular chain.
6. How do you declare an array in C?
An array is declared by specifying the type of its elements and the number of elements it will hold. The general syntax for declaring an array is:
type arrayName[arraySize];
Here,
- type: The data type of the elements in the array (e.g., int, float, char).
- arrayName: The name you want to give to the array.
- arraySize: The number of elements the array can hold.
7. Differentiate between a stack and a queue.
This is one of the most commonly asked data structures (DS) interview questions. The key differences between a stack and a queue are as follows:
| Aspect | Stack | Queue |
|---|---|---|
| Definition | A linear data structure that follows the Last In, First Out (LIFO) principle. | A linear data structure that follows the First In, First Out (FIFO) principle. |
| Order of Operations | The most recently added element is the first to be removed. | The earliest added element is the first to be removed. |
| Insertion Operation | push – Adds an element to the top of the stack. | enqueue – Adds an element to the end of the queue. |
| Deletion Operation | pop – Removes the element from the top of the stack. | dequeue – Removes the element from the front of the queue. |
| Access | Access is restricted to the top element only. | Access is restricted to both the front and the end of the queue for dequeue and enqueue operations, respectively. |
| Use Cases | Function call management, undo mechanisms, expression evaluation. | Scheduling tasks, buffering, and queue management in algorithms. |
| Examples | Browser history (back and forward), stack-based algorithms (e.g., depth-first search). | Print spooling, task scheduling in operating systems, breadth-first search. |
| Implementation | Often implemented using arrays or linked lists with a top pointer. | Often implemented using arrays or linked lists with front and rear pointers. |
| Complexity | Operations (push and pop) are O(1) in time complexity. | Operations (enqueue and dequeue) are O(1) in time complexity. |
8. What do you understand by recursion?
Recursion in programming is a technique where a function calls itself in order to solve a problem. A recursive function typically breaks down a problem into smaller, more manageable sub-problems of the same type. It continues to call itself with these smaller sub-problems until it reaches a base case, which is a condition that terminates the recursion.
For example:
int factorial(int n) {
if (n <= 1) // Base case
return 1;
else // Recursive case
return n * factorial(n - 1);
}
9. How is a one-dimensional array different from a two-dimensional array?
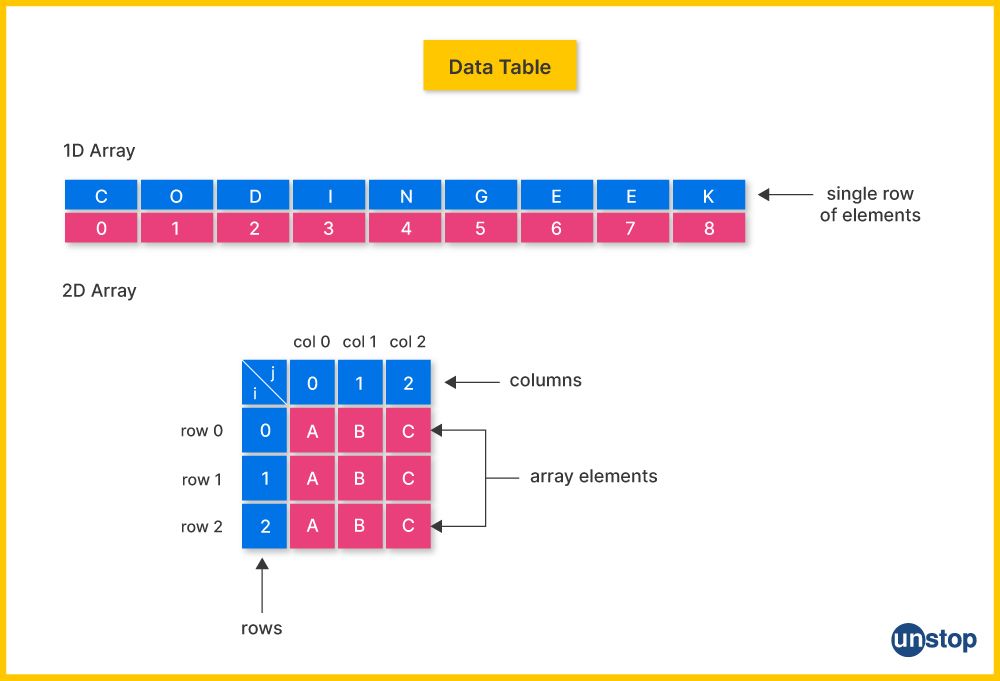
Listed below are the key differences between one-dimensional and two-dimensional arrays:
| Aspect | One-Dimensional Array | Two-Dimensional Array |
|---|---|---|
| Structure | Linear sequence of elements | Grid or matrix with rows and columns |
| Indexing | Single index (e.g., arr[i]) | Two indices (e.g., matrix[i][j]) |
| Size | Defined by a single size parameter (number of elements) | Defined by two size parameters (number of rows and columns) |
| Example | int arr[5] (array with 5 elements) | int matrix[3][4] (3 rows, 4 columns) |
| Accessing Elements | Access with one index | Access with two indices |
| Use Cases | Simple lists, such as lists of numbers or names | Tabular data, matrices, grids |
| Memory Layout | Contiguous memory block | Contiguous memory block, organized in a grid |
10. List the area of applications of data structure.
Here are some key areas where data structures play a crucial role:
-
Database Management Systems: Efficiently index and query data using structures like B-trees and hash tables.
-
File Systems: Organize and manage files with directory trees and allocate storage with linked lists or bitmaps.
-
Networking: Handle data packets and optimize routing with queues and graphs.
-
Operating Systems: Manage memory and schedule processes using structures like linked lists and queues.
-
Compilers: Parse code and manage symbols with trees and hash tables using compilation.
-
Search Engines: Index and retrieve search results using hash tables and inverted indexes.
-
Graphics and Image Processing: Manage graphical data with spatial structures like quadtrees.
-
AI and Machine Learning: Implement decision-making and model relationships with trees and graphs.
-
Web Development: Cache data and manage sessions using hash maps and lists.
-
Game Development: Manage game states and pathfinding with trees and graphs.
-
Bioinformatics: Store and analyze genetic data using specialized data structures.
-
Finance and Trading: Handle portfolios and trading algorithms with efficient data structures.
11. What is the difference between file structure and storage structure?
File structure and storage structure are related but distinct concepts in data management and computer science. Here’s a comparison of the two:
| Aspect | File Structure | Storage Structure |
|---|---|---|
| Definition | Refers to the organization and layout of data within a file. It defines how data is logically arranged and accessed. | Refers to how data is physically stored on a storage medium (e.g., hard drive, SSD). It involves the low-level organization of data blocks. |
| Purpose | To manage how data is organized and retrieved from a file. It often focuses on logical aspects such as records and fields. | To manage the efficient use of physical storage space and retrieval operations, focusing on the physical arrangement of data blocks or sectors. |
| Examples |
Sequential File Structure: Data is stored in a linear sequence. |
Block Storage: Data is stored in fixed-size blocks. |
| Focus | Logical organization of data to facilitate access and manipulation. | Physical layout and efficient management of storage space. |
| Usage | Implemented in file systems and database management systems to organize how data is saved and retrieved. | Implemented by storage devices and file systems to manage the actual data storage process. |
12. What is the significance of multidimensional arrays?
Multidimensional arrays are a type of data structure used to represent and manage data in more than one dimension. They extend the concept of one-dimensional arrays by allowing us to store data in a tabular format or higher-dimensional structures (array of arrays). Here’s why they are significant:
-
Representation of Complex Data: Multidimensional arrays are ideal for sequential representation of tables, matrices, or grids, where data is organized in rows and columns. For example, a 2D array can represent a matrix in mathematical computations or a game board in a simulation.
-
Efficient Data Access: They provide a way to access elements efficiently using indices. For instance, in a 2D array, you can quickly access any element using its row and column indices.
-
Spatial Data Handling: Useful in applications involving spatial data such as geographical maps, image processing (where a 2D array represents pixel values), and simulations.
-
Multi-dimensional Problems: Multidimensional arrays can handle higher-dimensional problems (e.g., 3D arrays for volumetric data or simulations in three dimensions), which are common in scientific computations, physics simulations, and complex data analysis.
-
Simplified Code: They simplify the code needed for managing complex data structures by allowing data to be organized and accessed in a systematic way. This can make algorithms more straightforward and easier to implement.
-
Algorithm Efficiency: Certain algorithms, like those in dynamic programming, can be implemented more efficiently using multi-dimensional arrays to store intermediate results and facilitate faster computations.
13. What do you understand by time complexity in data structures and algorithms?
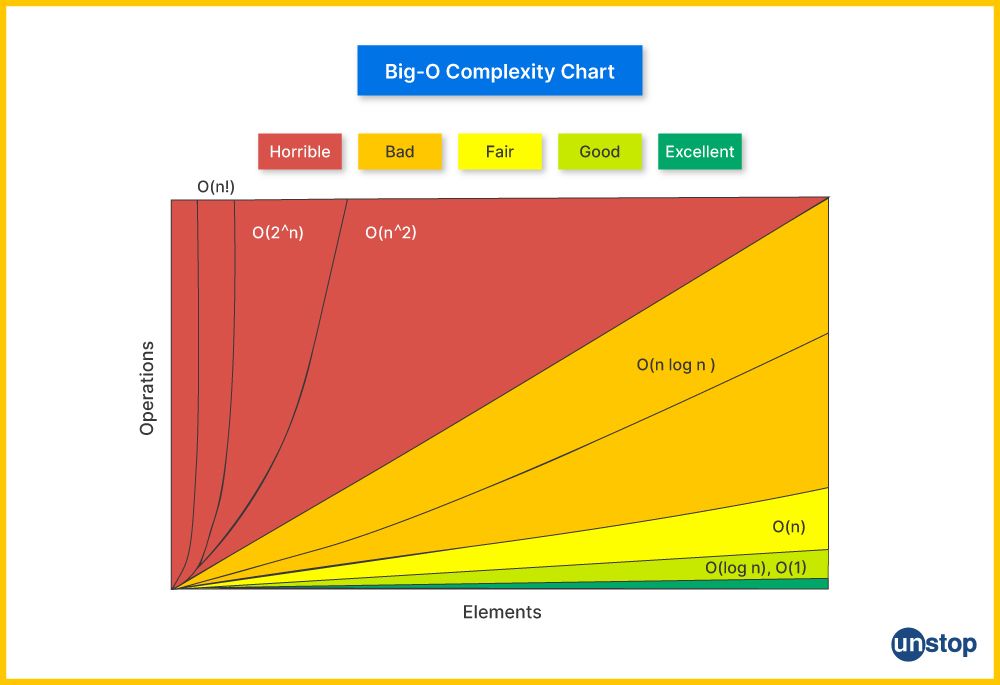
Time Complexity in data structures measures how the execution time grows as the input size increases. It provides an estimate of the algorithm's efficiency and is used to compare the performance of different coding algorithms.
The most common way to express time complexity is using Big-O notation (O(f(n))), which describes the upper bound of the runtime in the worst-case scenario. It provides an asymptotic analysis of how the runtime increases with input size.
Common Complexities:
- O(1): Constant time, i.e., the runtime does not change with the size of the input. Example: Accessing an element in an array.
- O(log n): Logarithmic time, i.e., the runtime increases logarithmically with the input size. Example: Binary search.
- O(n): Linear time, i.e., the runtime increases linearly with the input size. Example: Linear search.
14. Discuss the advantages and disadvantages of using arrays.
Arrays are one of the most basic and commonly used data structures in computer science. They provide a straightforward way to store and access a collection of elements. Here's a discussion of the advantages and disadvantages of arrays:
Advantages of Arrays:
- Direct Access: Provides O(1) time complexity for accessing elements via indexing.
- Simple Implementation: Easy to implement and use with contiguous memory allocation.
- Cache Efficiency: Stores elements contiguously, improving cache performance.
- Fixed Size: Predictable memory usage when the size is known in advance.
- Ease of Use: Built-in support in most programming languages.
Disadvantages of Arrays:
- Fixed Size: Cannot dynamically resize, leading to potential wasted or insufficient space.
- Costly Insertions/Deletions: Inserting or deleting elements (except at the end) requires shifting elements, resulting in O(n) time complexity.
- Memory Usage: Can waste memory space if not fully utilized or require resizing if too small.
- Static Nature: Less suitable for dynamic data sizes and frequent changes.
- Lack of Flexibility: Inefficient for operations like searching or resizing without additional algorithms.
Data Structures Interview Questions: Intermediate
15. What is a depth-first search (DFS)?
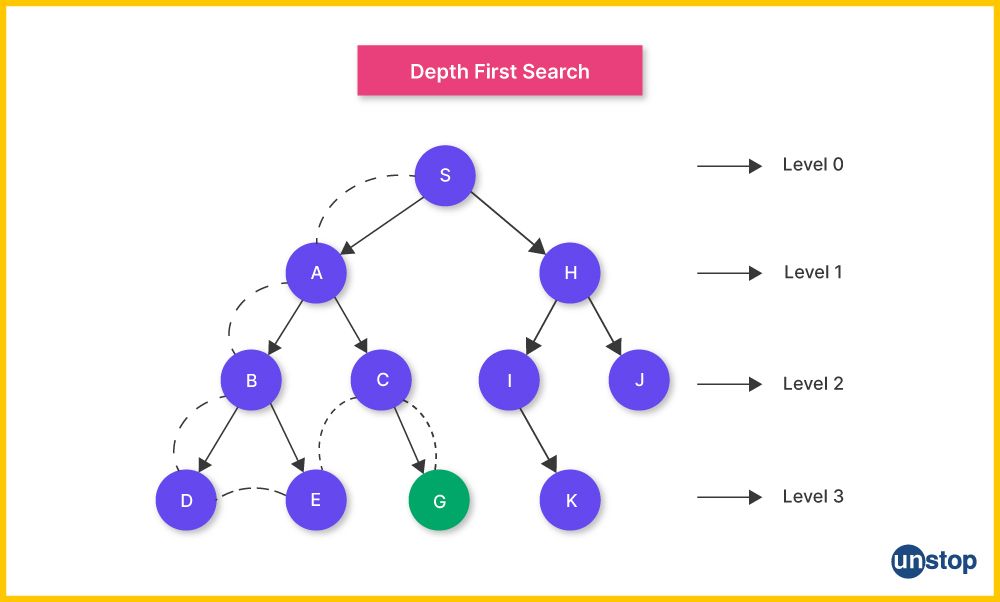
Depth-first search (DFS) is a fundamental algorithm used for traversing or searching tree or graph data structures. The main idea behind DFS is to explore as far down a branch as possible before backtracking.
Working:
- Starting Point: Begin at a selected node (root or any arbitrary node) and mark it as visited.
- Explore: Recursively explore each unvisited adjacent node, moving deeper into the structure.
- Backtrack: Once a node has no more unvisited adjacent nodes, backtrack to the previous node and continue the process.
- Continue: Repeat the process until all nodes in the structure have been visited.
Key Features:
- Stack-Based: DFS can be implemented using a stack data structure, either explicitly with a stack or implicitly via recursion.
- Traversal Order: Visits nodes in a depthward motion before moving horizontally. This means it explores all descendants of a node before visiting its siblings.
16. Explain the working mechanism of linear search.
Linear search is a simple searching algorithm used to find a specific element in a list or array. It works by sequentially checking each element until the desired element is found or the end of the list is reached.
Working Mechanism of Linear Search:
-
Start from the Beginning: Begin at the first element of the list or array.
-
Compare Elements: Compare the target value (the element we are searching for) with the current element in the list.
-
Check for Match:
- If Match Found: If the target value matches the current element, return the index or position of that element.
- If No Match: If the target value does not match the current element, move to the next element in the list.
-
Repeat: Continue the comparison process until either:
- The target value is found, or
- The end of the list is reached without finding the target.
-
End of Search:
- If Target Found: Return the index or position of the target element.
- If Target Not Found: Return a value indicating that the target is not present in the list (e.g., -1 or null).
Example: Consider searching for the value 7 in the array [2, 4, 7, 1, 9]:
- Start at index 0: Check 2 (no match).
- Move to index 1: Check 4 (no match).
- Move to index 2: Check 7 (match found).
- Return index 2 as the position where the target value 7 is found.
17. Describe the characteristics of a queue data structure.
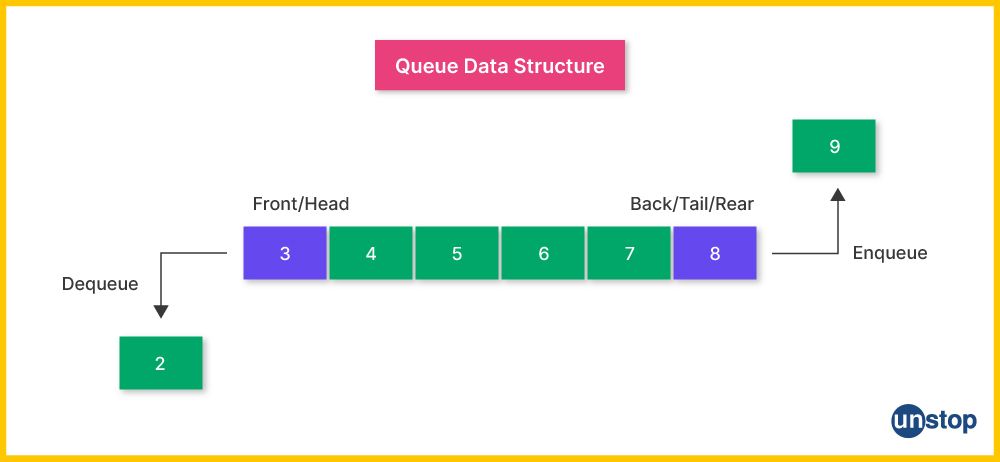
A queue is a data structure that follows the First In, First Out (FIFO) principle. Key characteristics include:
- FIFO (First In, First Out): The elements are pushed at the back (enqueue) and pulled from the front (dequeue). The first added element is the first to be replaced.
- Linear Structure: A sequence of elements in order to be taken up in succession (queue).
- Enqueue and Dequeue Operations: This data structure operates with two main functions, namely, the enqueue, which implies adding to the end, and the dequeue, which involves taking away from the beginning.
- Limited Access: Access to elements is typically restricted, and accessing elements often occurs sequentially.
18. What is the difference between heap and priority queue?
A heap and a priority queue are closely related but distinct concepts in data structures. While heaps are often used to implement priority queues, they are not synonymous. Here are the key differences between the two:
| Aspect | Heap | Priority Queue |
|---|---|---|
| Definition | A binary tree-based data structure that maintains a specific order property (min-heap or max-heap). | An abstract data structure that allows the insertion of elements with associated priorities and supports efficient retrieval of the highest (or lowest) priority element. |
| Purpose | Used to efficiently manage and retrieve the minimum or maximum element. | Provides a way to manage elements with priorities and retrieve the element with the highest or lowest priority efficiently. |
| Implementation | Typically implemented using an array-based binary tree. | Often implemented using a heap (min-heap or max-heap) or other data structures like balanced trees. |
| Operations |
Insert: Add a new element while maintaining heap property. |
Insert: Add an element with a priority. Extract-Min/Max: Remove and return the element with the highest or lowest priority. Peek: Access the element with the highest or lowest priority. |
| Order Property | Maintains a partial order where each node is smaller (min-heap) or larger (max-heap) than its children. | Maintains a priority order, where the element with the highest (or lowest) priority is always accessible. |
| Use Cases |
Heap Sort: Efficient sorting algorithm. |
Task Scheduling: Managing tasks with priorities. |
19. What is a sorted list, and how is it advantageous in certain scenarios?
A sorted list is a list in which elements are arranged in a specific order, typically ascending or descending. The ordering can be based on a natural ordering of the elements (like numerical or lexicographical order) or defined by a custom comparator. The sorting can be done automatically upon insertion of elements or performed once all elements are added.
Advantages:
-
Efficient Searching: A sorted list allows for binary search, which is much faster than linear search. Binary search has a time complexity of O(logn)O(\log n)O(logn), compared to O(n)O(n)O(n) for linear search. This is particularly beneficial for large datasets.
-
Easy to Maintain Order: While maintaining order during insertion and deletion can be challenging, some data structures like balanced binary search trees or skip lists support efficient insertion and deletion while maintaining order. In simpler cases, maintaining order may require re-sorting or shifting elements, which can be less efficient.
-
Improved Performance in Specific Operations: Certain algorithms and operations are more efficient when working with sorted data. For example, algorithms for merging, finding duplicate elements, or computing ranges (like finding the range of elements within a specific interval) can be performed more efficiently on sorted lists.
20. What is a sparse matrix?
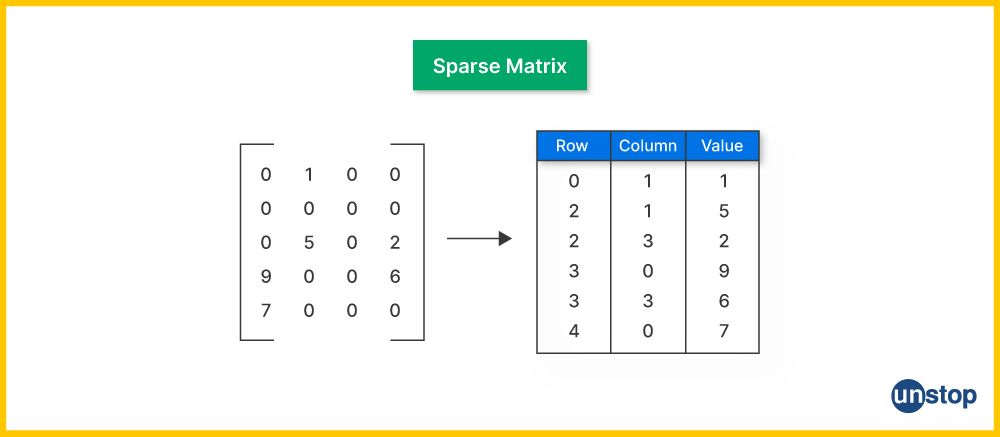
A sparse matrix is a matrix in which most of the elements are zero. This type of matrix is commonly used in mathematical computations and data storage where the non-zero elements are significantly fewer compared to the total number of elements. Its common storage formats are as follows:
-
Compressed Sparse Row (CSR):
- Stores non-zero elements in a single array.
- Uses two additional arrays to store the column indices of the non-zero elements and the row pointers, which indicate the start of each row in the non-zero elements array.
-
Compressed Sparse Column (CSC):
- Similar to CSR, but it stores non-zero elements in a column-wise manner.
- Uses arrays to store the row indices of the non-zero elements and the column pointers, which indicate the start of each column in the non-zero elements array.
-
Coordinate List (COO):
- Stores a list of tuples where each tuple contains the row index, column index, and the value of each non-zero element.
-
List of Lists (LIL):
- Each row is represented as a list of non-zero elements and their column indices. This format is often used for constructing matrices incrementally.
21. Discuss the concept of dynamic memory allocation. Why is it important in programming?
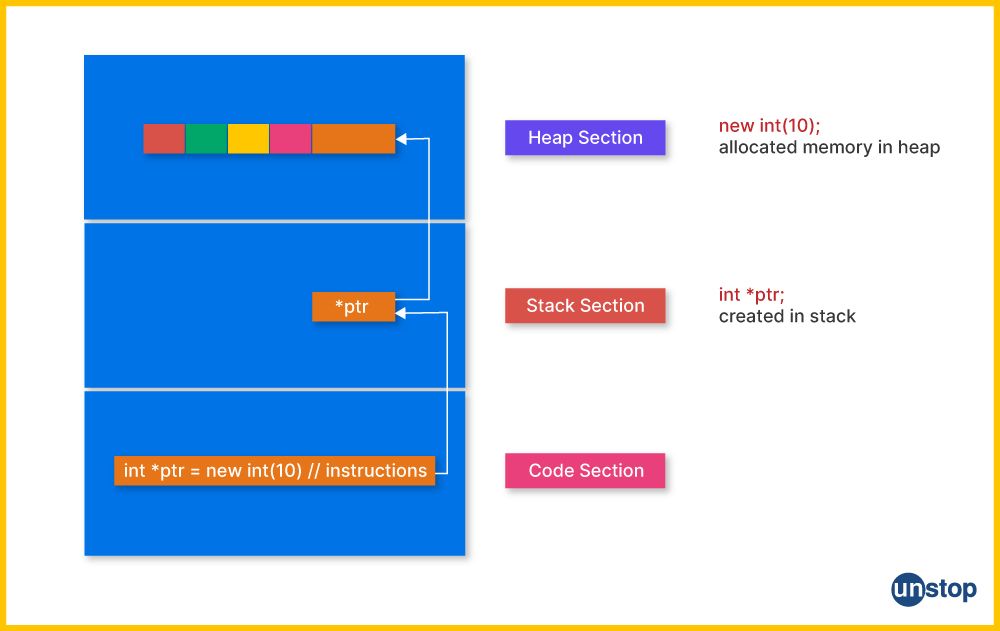
Dynamic memory allocation refers to the process of allocating memory storage during the runtime of a program, rather than at compile time. This is done using functions or different operators provided by programming languages, such as malloc(), calloc(), realloc(), and free() in C, or the new and delete operators in C++.
In languages with automatic memory management, like Python or Java, dynamic memory allocation is managed by the language's runtime environment through a process known as garbage collection.
Importance:
- Flexibility: Allocates and reallocates memory dynamically in response to the data storage sizes.
- Optimized Memory Usage: It also assists in minimizing wastage through the allocation of an appropriate size of memory that is needed.
- Dynamic Data Structures: Provides support for developing linked lists and trees as dynamic data structures.
22. What is the difference between a depth-first search and a breadth-first search?
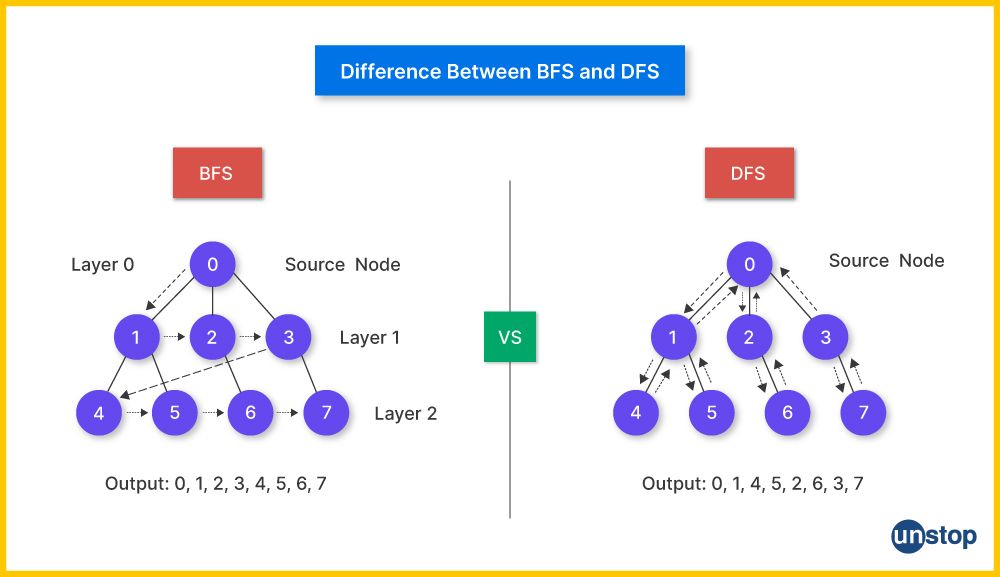
This is one of the most commonly asked data structures and algorithms interview questions. Given below is a detailed comparison between Depth-First Search and Breadth-First Search:
| Feature | Depth-First Search (DFS) | Breadth-First Search (BFS) |
|---|---|---|
| Traversal Method | Explores as far down a branch as possible before backtracking. | Explores all neighbors at the present depth before moving on to nodes at the next depth level. |
| Data Structure Used | Stack (can be implemented using recursion). | Queue |
| Time Complexity | O(V + E) where V is the number of vertices and E is the number of edges. | O(V + E) where V is the number of vertices and E is the number of edges. |
| Space Complexity | O(h) where h is the maximum depth of the tree (or recursion stack size). | O(w) where w is the maximum width of the tree or graph (i.e., the largest number of nodes at any level). |
| Traversal Order | Visits nodes deeper into the tree or graph first. | Visits nodes level by level, starting from the root. |
| Finding Shortest Path | Not guaranteed to find the shortest path in unweighted graphs. | Guarantees finding the shortest path in unweighted graphs. |
| Applications | Used for topological sorting, solving puzzles (e.g., mazes), and detecting cycles. | Used for finding shortest paths, broadcasting, and level-order traversal. |
| Algorithm Implementation | Simple to implement recursively or using an explicit stack. | Typically implemented using a queue, iteratively. |
23. Explain the pop operation in the context of a stack data structure.
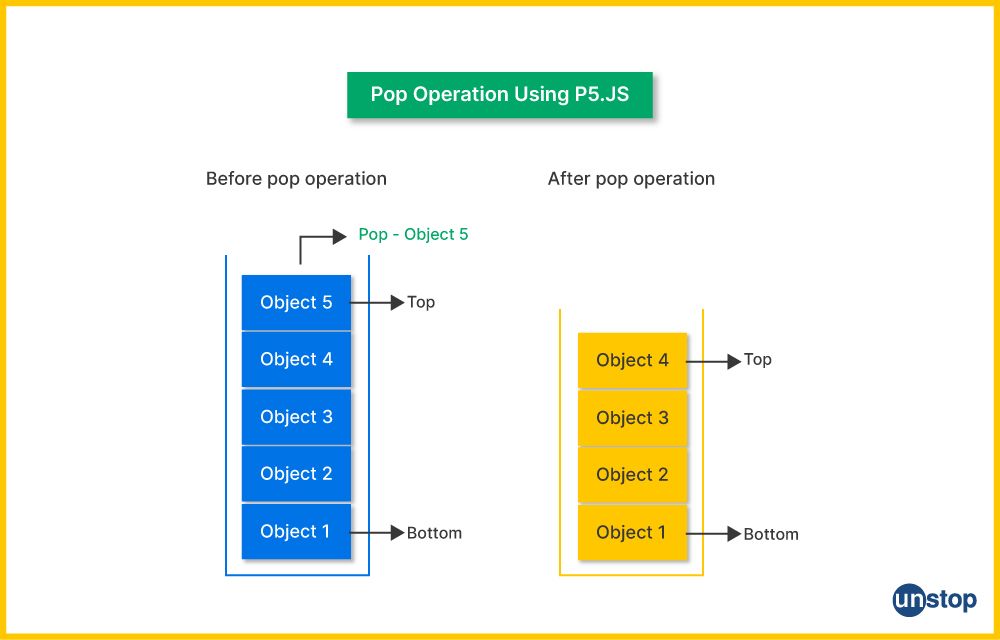
In the context of a stack data structure, the pop operation refers to removing the top element from the stack.
-
Removes Top Element: The pop operation takes away the element that is currently at the top of the stack.
-
Follows LIFO Principle: The last element added is the first one to be removed.
-
Returns Removed Element: Usually returns the value of the top element that is removed.
-
Time Complexity: It operates in constant time, O(1), which means it’s quick regardless of how many elements are in the stack.
-
Handling Empty Stack: If the stack is empty, trying to pop may either cause an error in code or return a special value indicating the stack is empty.
Example:
Stack before pop: [10, 20, 30]
pop operation removes 30
Stack after pop: [10, 20]
24. What is a double-ended queue, and how does it differ from a regular queue?
A double-ended queue (deque) is a data structure that allows the insertion and removal of elements from both ends, whereas a regular queue allows operations only at one end (rear for insertion) and the other end (front for removal).
Key Differences:
- Insertion/Removal Flexibility: Deques allow insertion and removal from both ends, while regular queues allow these operations only at one end each.
- Usage: Deques are more versatile and can be used in scenarios requiring operations at both ends, whereas regular queues are used for simple FIFO processing.
- Flexibility: Deques are more suitable than ordinary queues in such applications as queuing and stacking.
25. Explain the concept of space complexity in algorithms.
Space complexity in algorithms measures the total amount of memory required to execute an algorithm relative to the size of the input data.
- It includes both the fixed amount of space needed for program instructions and the variable space used for dynamic data structures, such as arrays or linked lists.
- Expressed in Big-O notation (e.g., O(1), O(n), O(n^2)), space complexity helps in understanding how the memory requirements grow as the input size increases.
- For instance, an algorithm with constant space complexity (O(1)) uses a fixed amount of memory regardless of input size, while an algorithm with linear space complexity (O(n)) uses memory proportional to the input size.
26. How does a stack data structure work?
A stack is a fundamental data structure that operates on a Last-In-First-Out (LIFO) principle, meaning the most recently added element is the first one to be removed. A stack works as follows:
-
LIFO Principle: The last element added to the stack is always the first one to be removed. This behavior is akin to a stack of plates where you can only take the top plate off or add a new plate on top.
-
Operations: A stack supports the following set of core operations:
- Push: Add an element to the top of the stack. This operation increases the stack's size by one.
- Pop: Remove the element from the top of the stack. This operation decreases the stack's size by one and returns the removed element.
- Peek/Top: View the element at the top of the stack without removing it. This operation allows you to examine the most recently added element.
- IsEmpty: Check whether the stack is empty. This operation returns a boolean value indicating if there are no elements in the stack.
27. Describe the applications of graph data structure.
Graphs are versatile data structures with a wide range of applications across various fields. Here are some key applications:
-
Social Networks:
- Friendship and Relationship Mapping: Represent users as vertices and connections (friendships, follows) as edges to model social interactions and network dynamics.
- Recommendation Systems: Use graph algorithms to suggest friends or content based on connections and interests.
-
Routing and Navigation:
- Shortest Path Algorithms: Algorithms like Dijkstra's and A* are used for finding the shortest paths between locations on maps or within networks.
- Traffic Management: Model and analyze road networks to optimize traffic flow and route planning.
-
Web Page Link Analysis:
- Search Engines: Use graphs to represent web pages and hyperlinks, applying algorithms like PageRank to rank pages based on their importance and link structure.
- Crawling: Efficiently navigate and index the web by following links represented in a graph.
-
Network Design and Analysis:
- Communication Networks: Design and optimize communication and data transfer networks such as telephone or internet networks.
- Reliability Analysis: Evaluate the robustness and redundancy of networks to prevent failures and improve connectivity.
-
Resource Allocation and Scheduling:
- Task Scheduling: Represent tasks and their dependencies as a directed acyclic graph (DAG) to schedule and manage project tasks effectively.
- Job Scheduling: Optimize the allocation of resources and scheduling of jobs in systems like operating systems or manufacturing processes.
-
Biological Networks:
- Protein-Protein Interaction: Model interactions between proteins or genes to understand biological processes and functions.
- Ecosystem Modeling: Represent species and their interactions in an ecosystem to study relationships and dynamics.
-
Games and Simulations:
- Pathfinding: Use graph algorithms for navigation and movement in game environments, such as finding the shortest path for characters.
- Game State Modeling: Represent game states and transitions as a graph to manage and analyze game mechanics and strategies.
-
Circuit Design and Analysis:
- Electronic Circuits: Model circuits as graphs with critical components as nodes and connections as edges to analyze and optimize circuit design.
- Network Analysis: Evaluate the performance and behavior of electrical and electronic networks.
-
Graph Theory in Research:
- Algorithm Development: Develop new algorithms and techniques based on graph theory for various computational problems.
- Mathematical Modeling: Use graph theory to solve problems in mathematics and computer science.
28. Explain the process of the selection sort algorithm.
Selection sort is a simple, comparison-based sorting algorithm that works by repeatedly finding the minimum (or maximum) element from the unsorted portion of the list and moving it to the beginning. It is easy to understand and implement but is generally inefficient on large lists compared to more advanced algorithms like quicksort or mergesort.
Process of Selection Sort:
-
Initialization: Start with the entire list as the unsorted portion.
-
Find the Minimum Element: Traverse the unsorted portion of the list to find the smallest (or largest) element.
-
Swap with the First Unsorted Element: Swap this minimum element with the first element of the unsorted portion.
-
Update the Boundary: Move the boundary of the sorted portion one step forward, effectively expanding the sorted portion and shrinking the unsorted portion.
-
Repeat: Repeat steps 2 to 4 for the remaining unsorted portion until the entire list is sorted.
29. What is the time complexity of linked list operations?
The time complexity of various operations on a linked list depends on the type of linked list (singly linked, doubly linked, or circular) and the specific operation being performed. Here's a summary of the time complexity for common operations on a linked list:
| Operation | Singly Linked List | Doubly Linked List | Circular Linked List |
|---|---|---|---|
| Access (Get) | O(n) | O(n) | O(n) |
| Insertion at Head | O(1) | O(1) | O(1) |
| Insertion at Tail | O(n) | O(1) | O(1) |
| Insertion After Node | O(n) | O(n) | O(n) |
| Deletion at Head | O(1) | O(1) | O(1) |
| Deletion at Tail | O(n) | O(1) | O(n) |
| Deletion by Value | O(n) | O(n) | O(n) |
| Search | O(n) | O(n) | O(n) |
30. Explain the concept of a hash table. How does it handle collisions?
This is one of the popularly asked data structures interview questions. A hash table is a data structure that implements an associative array, mapping keys to values. It uses a hash function to compute an index (also called a hash code) into an array of buckets or slots, from which the desired value can be found. This allows for efficient data retrieval, typically in constant time, O(1), for both average-case insertion and lookup operations.
- Collision Handling: Collisions occur when two different keys hash to the same index in the array. Various strategies exist to handle collisions:
-
Chaining: Each bucket points to a linked list of entries that share the same hash index. When a collision occurs, a new entry is added to the list. Searching for an entry involves traversing the linked list.
-
Open Addressing: Instead of linked lists, open addressing stores all elements in the hash table array itself. When a collision occurs, the algorithm probes the array to find an empty slot using methods like linear probing, quadratic probing, or double hashing.
-
Double Hashing: Uses two hash functions to calculate the index and the step size, helping to avoid clustering of keys.
31. How is bubble sort implemented, and what is its time complexity?
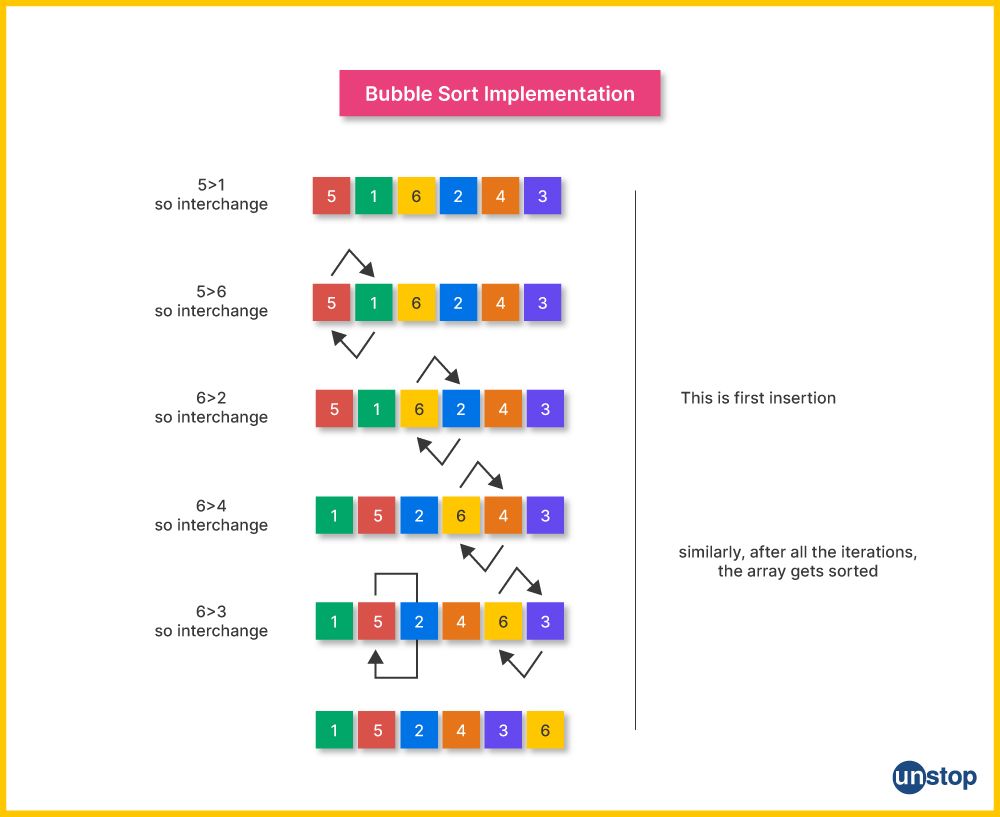
Bubble sort is a simple comparison-based sorting algorithm. Here's how it works:
- Starting from the beginning of the array, compare each pair of adjacent elements.
- Swap the elements if they are in the wrong order (i.e., the first element is greater than the second element).
- Repeat the process for each element in the array, moving from the start to the end.
- After each pass through the array, the largest unsorted element "bubbles up" to its correct position.
- Reduce the number of comparisons for the next pass since the largest elements are already sorted.
Time Complexity: O(n^2) in the worst and common case, in which 'n' is the variety of elements in the array. In the best case (while the array is already taken care of), it's miles O(n).
32. Discuss the limitations of bubble sorting and provide scenarios where it might be preferable over other sorting algorithms.
Despite its simplicity, bubble sort has several limitations:
- Inefficiency: Bubble kind is inefficient for huge datasets due to its quadratic time complexity.
- Lack of Adaptivity: It does not adapt properly to the present order of elements. It performs an identical variety of comparisons no matter the initial order.
- Not Suitable for Large Datasets: Due to its inefficiency, bubble kind isn't the best choice for sorting huge datasets or datasets with complicated systems.
Scenarios Where Bubble Sort Might Be Preferable:
- Educational Purposes: Due to its simplicity, bubble sort is regularly used to introduce the idea of sorting algorithms in academic settings.
- Small Datasets: For very small datasets, wherein simplicity is more vital than performance, bubble sort might be considered.
- Nearly Sorted Data: In instances where the statistics are sorted, bubble sort's adaptive nature in the nice-case situation may be an advantage.
In actual international scenarios, different extra green sorting algorithms like quicksort, mergesort, or heapsort are commonly favored over bubble type, particularly for large datasets.
33. What are the advantages and disadvantages of using a hash table for data storage?
Advantages of Hash Tables
-
Fast Access: Hash tables generally offer very fast insertion, deletion, and lookup operations, with an average time complexity of O(1) due to direct index calculation using the hash function.
-
Flexibility: They can store a wide variety of abstract data types and are versatile in handling different kinds of data.
-
Efficient Memory Usage: When the hash table is not too densely populated, it can be memory-efficient as it typically only stores the keys and values that are actually used.
-
Efficient Handling of Large Data: Hash tables can efficiently handle large sets of data because their operations do not depend significantly on the size of the data set.
Disadvantages of Hash Tables
-
Potential for Collisions: Collisions can degrade the performance of a hash table, especially if the hash function is not well-designed or if the table becomes too full. Poor collision handling can lead to O(n) time complexity in the worst case.
-
Memory Overhead: Hash tables require additional memory for storing pointers or linked lists (in chaining) or for handling probing sequences (in open addressing). They also typically require more space than the actual data being stored to avoid collisions (load factor management).
-
Difficulty in Traversal: Unlike data structures like arrays or linked lists, hash tables do not support efficient ordered traversal. The order of elements depends on the hash function, and there is no inherent way to traverse the elements in a particular order.
-
Complexity of Hash Functions: Designing an efficient hash function that minimizes collisions and distributes keys uniformly is often non-trivial. Poor hash functions can lead to clustering and degrade performance.
Data Structures Interview Questions: Advanced
34. What is the significance of a left node in a tree data structure, and how does it impact operations like searching and traversal in a binary search tree?
In a tree data structure, particularly a binary tree, a left node refers to the child node that is positioned to the left of a given parent node. The significance of the left node and how it impacts operations like searching and traversal can be understood more clearly within the context of a Binary Search Tree (BST).
Significance of a Left Node in a Binary Search Tree:
-
Binary Search Tree (BST) Property: In a BST, the left node of a given node contains values that are less than the value of the parent node. This property is crucial for maintaining the ordered structure of the tree and enables efficient search operations.
-
Search Operations: When searching for a specific value in a BST:
- If the value to be searched is less than the value of the current node, we move to the left child (left node) of the current node.
- This property allows us to eliminate half of the tree from consideration with each step, resulting in an average time complexity of O(log n) for balanced BSTs.
-
Traversal Operations: Different traversal methods use the left node in various ways:
- In-order Traversal: Visits the left subtree first, then the root, and finally the right subtree. This traversal method produces a sorted sequence of node values for BSTs.
- Pre-order Traversal: Visits the root first, then the left subtree, and finally the right subtree. In this order, the left node is processed before the right node.
- Post-order Traversal: Visits the left subtree first, then the right subtree, and finally the root. Here, the left node is processed before the right node and the root.
Impact on Operations:
-
Efficiency of Search: The left node helps maintain the BST property, allowing searches to be more efficient. By leveraging the property that all left children contain values less than their parent, we can quickly narrow down the search space.
-
Insertion and Deletion: When inserting or deleting nodes, the position of the left node plays a crucial role in maintaining the BST property. The new node must be placed in the correct position relative to existing nodes, and the tree may need to be rebalanced if it becomes unbalanced.
-
Balancing: In self-balancing trees like AVL trees or Red-Black trees, the left node’s role in maintaining balance is critical. These trees use rotations to keep the tree balanced and ensure that operations like search, insertion, and deletion remain efficient.
35. How does a binary search tree differ from a regular binary tree? Explain its advantages in terms of search operations.
Binary Search Tree (BST): A tree data structure in which each node has a maximum of two children, such that all entries in the left subtree are less than the node, while those of the right subtree have higher values than the node itself.
|
Aspect |
Regular Binary Tree |
Binary Search Tree |
|
Definition |
A tree data structure where each node has at most two children, but there are no specific rules regarding the values of nodes. |
A specific type of binary tree in which the left child contains values less than the parent and the right child contains values greater than the parent. |
|
Ordering of Nodes |
No specific ordering rule. Nodes can be arranged in any order. |
Maintains a strict ordering rule, ensuring that for any node, all nodes in its left subtree are less, and all nodes in its right subtree are greater. |
|
Searching |
Inefficient for searching as there are no ordering rules. Requires traversal of the entire tree. |
Efficient for searching due to the binary search property. Allows for logarithmic time complexity in average cases. |
|
Insertion and Deletion |
No specific rules for insertion and deletion. This can lead to unbalanced trees. |
Follows specific rules for insertion and deletion to maintain the binary search property. Ensures balance for optimal performance. |
|
Use Cases |
Used in scenarios where ordering is not essential and the focus is on hierarchical relationships. |
Ideal for scenarios requiring efficient searching, retrieval, and ordered representation of data, such as database indexing. |
|
Example
|
Generic tree structure without specific ordering. |
Search trees are used in applications where fast searching and retrieval are crucial, such as symbol tables and databases. |
Advantages in Search Operations:
- Efficient Search: A search is carried out more efficiently in a BST than in an ordinary binary tree because of its ordering property.
- Logarithmic Time Complexity: In a balanced BTS, search operations exhibit a time complexity of O(log n).
- Ease of Range Queries: A BST is simple and efficient in-range queries. Navigating through the tree following a certain order facilitates finding all elements in a certain range.
36. How is expression evaluation performed using a stack data structure? Provide an example of an expression and step through the evaluation process.
Expression evaluation using a stack data structure is a common method for processing mathematical expressions, particularly in postfix (Reverse Polish Notation) and infix expressions. The stack helps manage the operands and operators in a systematic way to evaluate expressions efficiently.
Process:
- Create two stacks: an operator array and another operand array.
- Do this for every symbol in the expression.
- Push the symbol onto the operand stack if it is an operand.
- Pop operations from the operand stack. If the symbol is an operator, apply the operator to operands and push the result on the operand stack.
- Repeat the process until the whole expression is completed.
- The last result ends on the operand stack.
Example: Consider the expression: 5+(3×8)-6/2. A step-by-step evaluation of this would be as follows:
Operand Stack: [5]
Operand Stack: [5], Operator Stack: ['+']
Operand Stack: [5, 3], Operator Stack: ['+']
Operand Stack: Operator stack: ‘+’, ’*’ [5, 3]
Operand Stack: [5, 24], Operator Stack: ['+']
Operand Stack: {5,24}, Operand Stack : {‘+’, ‘-’}
Operand Stack: Stck Op: [‘+’] [5, 24, 6]
Operand Stack: Operator stack: {[5/6]+}
Operand Stack: [5, 12], Operator Stack: ['+']
Operand Stack: [17], Operator Stack: []
Thus, the last value is 17.
37. Define and discuss the characteristics of a doubly-linked list.
A doubly-linked list is a type of linked list in which each node contains three components: a data element, a reference (or pointer) to the next node in the sequence, and a reference to the previous node. This structure allows traversal of the list in both forward and backward directions, unlike a singly-linked list, which can only be traversed in one direction.
Characteristics of a Doubly-Linked List
-
Bidirectional Links: Each node contains a pointer to the next node (called next) and a pointer to the previous node (called prev). This enables bidirectional traversal, allowing access to both the subsequent and preceding elements from any given node.
-
Node Structure: Each node typically consists of three parts: the data it holds, a reference to the next node, and a reference to the previous node. The structure can be visualized as:
| prev | data | next |
- Head and Tail Pointers: The list has a head pointer that points to the first node and a tail pointer that points to the last node. The prev pointer of the head node is usually set to null (or equivalent in other languages), and the next pointer of the tail node is also set to null.
- Dynamic Size: The size of a doubly-linked list can grow or shrink dynamically as elements are added or removed, unlike arrays, which have a fixed size.
- Insertion and Deletion: Insertion and deletion operations can be efficiently performed from both ends of the list as well as from any position within the list, provided a reference to the node is available. These operations typically involve adjusting a constant number of pointers, making them O(1) operations in the best case.
- Memory Overhead: Each node requires additional memory for storing two pointers (next and prev) compared to a singly-linked list, which only stores one pointer per node.
38. What is an AVL tree, and how does it address the issue of maintaining balance in binary search trees?
An AVL tree is a type of self-balancing binary search tree named after its inventors, Adelson-Velsky and Landis. It was the first dynamically balanced binary search tree and is designed to maintain a balanced tree structure, which ensures that the tree remains balanced at all times after insertions and deletions.
Addressing the Issue of Balance: In a standard binary search tree (BST), the structure can become unbalanced with skewed branches if elements are inserted in a sorted order. This leads to poor performance for search, insert, and delete operations. This degradation can lead to a worst-case time complexity of O(n) for these operations, where n is the number of nodes.
39. Explain the basic operations of a heap data structure. How does it differ from a binary search tree?
A heap is a specialized tree-based data structure that satisfies the heap property. There are two main types of heaps: min-heaps and max-heaps. The basic operations of heap data structures are as follows:
- Insertion (Heapify-Up): Adds a new element to the heap and keeps the heap property by evaluating the detail with its discern and swapping if necessary.
- Deletion (Heapify-Down): Removes the pinnacle detail from the heap, replaces it with the final element, and keeps the heap property by evaluating the detail with its children and swapping if essential.
Difference between heap data structure and binary search tree:
| Feature | Heap | Binary Search Tree (BST) |
|---|---|---|
| Definition | A binary tree-based data structure that satisfies the heap property (either min-heap or max-heap). | A binary tree where for each node, the left subtree has values less than the node's value and the right subtree has values greater. |
| Heap Property | Min-Heap: Parent nodes are less than or equal to their children. Max-Heap: Parent nodes are greater than or equal to their children. |
No specific ordering property for the entire tree; ordering is only maintained between parent and its immediate children. |
| Insertion Complexity | O(log n) due to heapify operations after insertion. | O(log n) on average; can be O(n) in the worst case if the tree is unbalanced. |
| Deletion Complexity | O(log n) for removing the root (heap extraction), followed by heapify. | O(log n) for balanced BSTs; can be O(n) in the worst case for unbalanced trees. |
| Access to Minimum/Maximum | O(1) time for min-heap (min element at the root). O(1) time for max-heap (max element at the root). |
O(log n) on average; traversal is needed to find minimum or maximum values. |
| Search Complexity | O(n); requires linear search as there is no specific order. | O(log n) on average for balanced BSTs; can be O(n) in the worst case for unbalanced trees. |
| Balancing | Not necessarily balanced. No inherent mechanism to balance the tree. | Self-balancing variants like AVL trees or Red-Black trees maintain balance for better search efficiency. |
| Structure | Complete binary tree; all levels are fully filled except possibly the last, which is filled from left to right. | Binary tree; nodes are arranged based on value, and the structure is not strictly complete. |
| Use Cases | Priority queues, heap sort, scheduling algorithms. | Searching, sorting, in-order traversal for ordered data, hierarchical data representation. |
| Traversal | Traversal is not typically used or required for heaps. | In-order traversal gives sorted order; also supports pre-order and post-order traversal. |
40. What are the key use cases for a heap?
The key uses for a heap are as follows:
- Priority Queues: Heaps are typically used to implement priority queues where factors with better precedence (or decreased priority, depending on the heap type) are dequeued first.
- Heap Sort: Heaps can be used to implement an in-region sorting algorithm called Heap Sort.
- Dijkstra's Shortest Path Algorithm: Heaps are applied to implement algorithms like Dijkstra's shortest path algorithm efficiently.
- Task Scheduling: Heaps can be hired in mission scheduling algorithms wherein duties with higher priority are finished first.
41. Describe the structure and advantages of using an adjacency list in graph representation. Compare it with an adjacency matrix in terms of space and time complexity.
An adjacency list represents a graph as an array of connected lists or arrays. Each detail within the array corresponds to a vertex, and the connected listing or array related to every vertex incorporates its neighboring vertices (adjacent vertices).
Advantages:
- Space Efficiency: This is especially beneficial for sparse graphs (with fewer edges) because it stores facts about existing edges.
- Memory Efficiency: Consumes less reminiscence than an adjacency matrix for sparse graphs.
- Ease of Traversal: Iterating over the buddies of a vertex is simple and green.
Comparison with Adjacency Matrix:
Space Complexity:
- Adjacency List: O(V E), where V is the wide variety of vertices and E is the number of edges. It's extra green for sparse graphs.
- Adjacency Matrix: O(V^2), where V is the number of vertices. It becomes more area-inefficient for massive graphs and is suitable for dense graphs.
Time Complexity:
- Adjacency List: O(V E), where V is the range of vertices and E is the variety of edges between nodes. This illustration is efficient for traversing the entire graph or finding the friends of a selected vertex.
- Adjacency Matrix: O(V^2). Traversing the complete matrix is time-consuming, making it less efficient for sparse graphs.
42. How are the elements of a 2D array stored in the memory?
The elements of a 2D array are stored in a contiguous block of memory, with the layout depending on the language and its specific implementation. The two primary storage layouts for 2D arrays are row-major order and column-major order.
Row-Major Order: In row-major ordering, a 2D array’s rows are stored consecutively in memory. This means the entire first row is stored first, followed by the entire second row, and so forth, continuing until the final row is saved.
Column-Major Order: In column-major ordering, the 2D array’s columns are stored consecutively in memory. This means the entire first column is saved first, followed by the entire second column, and so on, until the final column is fully recorded.
43. Explain the concept of an expression tree and its significance in evaluating prefix expressions. How does a preorder traversal help in processing the tree efficiently?
An expression tree is a binary tree used to symbolize expressions in a way that helps their evaluation. Each leaf node represents an operand, and every non-leaf node represents an operator. The tree structure reflects the hierarchical order of operations.
Significance in Evaluating Prefix Expressions
- In a prefix expression, the operator precedes its operands, making it hard to evaluate directly.
- The expression tree allows a natural illustration of the expression's structure, simplifying the assessment technique.
Preorder Traversal for Efficient Processing
- Preorder traversal is an effective manner to manner an expression tree.
- During preorder traversal, the algorithm visits the foundation node first, then the left subtree, and sooner or later, the right subtree.
- In the context of expression bushes, appearing preorder traversal corresponds to traversing the expression in prefix notation.
Efficiency in Processing
- Preorder traversal helps process the expression tree efficaciously by allowing the set of rules to go to and compare nodes in the appropriate order. This order is primarily based on the expression's prefix notation.
- As the traversal encounters operators at the root of subtrees, it may carry out the corresponding operation on the values of the operands.
44. Discuss the advantages and disadvantages of using a deque data structure with two-way data access.
A deque (short for double-ended queue) is a data structure that allows insertion and deletion of elements from both the front and the back. It combines features of both stacks and queues. Here’s a look at the advantages and disadvantages of using a deque:
Advantages:
-
Flexible Access: Deques support efficient access and modification of elements at both ends. This versatility makes them suitable for a variety of applications where elements may need to be added or removed from either end.
-
Efficient Operations: Insertions and deletions at both ends of a deque are generally performed in constant time, O(1). This is beneficial for algorithms that require frequent additions or removals from both ends.
-
Use Cases: Deques can be used to implement both stacks (LIFO) and queues (FIFO). This dual capability makes them versatile for various algorithmic problems and data manipulation tasks.
-
Memory Efficiency: When implemented with a circular buffer or a doubly linked list, deques can efficiently use memory and avoid issues like memory fragmentation that might occur with some other data structures.
-
Algorithmic Flexibility: Deques are useful in scenarios that require operations like sliding window algorithms, where elements are continuously added and removed from both ends.
Disadvantages:
-
Complexity in Implementation: Depending on the underlying implementation (e.g., circular buffer, doubly linked list), deques can be more complex to implement compared to simpler data structures like arrays or linked lists.
-
Memory Overhead: When using certain implementations, such as doubly linked lists, deques may incur additional memory overhead for storing pointers (next and previous nodes), which can be less efficient in terms of space compared to contiguous memory storage.
-
Performance Variability: In some implementations, especially those based on arrays with resizing, operations at the ends might not always be constant time. For example, resizing the array can involve copying elements, which affects performance.
-
Cache Locality: Deques implemented with linked lists may suffer from poor cache memory locality compared to contiguous memory structures like arrays, potentially leading to slower access times due to cache misses.
45. Differentiate between a push operation in a stack and a push operation in a costly stack. How does the choice of push implementation impact the overall efficiency of stack-based algorithms?
Push Operation in a Stack:
- Standard Push: Adds a detail to the pinnacle of the stack.
- Time Complexity: O(1) - steady time, assuming sufficient area is to be had.
Push Operation in a Costly Stack:
- Costly Push: Adds a detail to the bottom of the stack.
- Time Complexity: O(n) - linear time, wherein 'n' is the number of factors in the stack because it involves rearranging present factors.
Impact on Overall Efficiency:
- Standard Push:
- Efficient and constant time.
- Ideal for maximum stack-primarily based algorithms.
- Costly Push:
- It's inefficient for huge stacks.
- Results in a substantial growth in time complexity.
- It can degrade the general performance of stack-based total algorithms.
Choice of Push Implementation:
- The preference depends on the algorithm's precise requirements and the facts' characteristics.
- For maximum situations, a trendy push operation with constant time complexity is preferred for retaining green stack-based algorithms.
- A luxurious push operation is probably considered in unique conditions where the order of elements wishes to be preserved, and the set of rules needs a bottom-to-pinnacle technique.
46. In the context of storage units and memory size, elaborate on the considerations for memory utilization in a static data structure. Compare this with the memory utilization in a hash map.
Static Data Structures are data structures with a fixed size determined at compile-time. Examples include arrays and fixed-size matrices.
Considerations for Memory Utilization in a Static Data Structure:
- Fixed Size: The shape's length is predetermined and can not be altered throughout runtime.
- Memory Efficiency: Memory is allocated statically, keeping off dynamic memory management overhead.
- Predictable Memory Usage: The memory footprint is thought earlier, assisting in memory-making plans.
Comparison with a Hash Map:
- Dynamic Size: Can dynamically resize to house changing records requirements.
- Memory Overhead: May eat extra memory for dealing with collisions and resizing.
- Flexible Memory Usage: Can develop or cut back based totally on the range of elements.
47. How can recursive functions be applied to efficiently process a list of nodes representing file directories and files?
Recursive functions are highly effective for processing hierarchical data structures like file directories and files due to their natural fit with the recursive nature of file systems. Each directory can contain other directories and files, which can be represented as nested structures. Here's how recursive functions can be applied to efficiently process such data:
-
Directory Traversal: A directory can contain files and subdirectories. Each subdirectory itself may contain files and more subdirectories. This forms a tree-like structure where each directory is a node that can have children (files and subdirectories).
- We can use recursion to traverse this hierarchical structure.
- The function processes the current directory and then recursively processes each subdirectory.
-
Operations:
- Listing Files and Directories: Recursively traverse each directory to list all files and subdirectories.
- Calculating Total Size: Recursively calculate the total size of files in a directory and all its subdirectories.
- Searching for Files: Recursively search for files that match certain criteria (e.g., file type, name).
48. Explain the concept of a deque data structure with two-way data access. How does the presence of a left child in a tree structure affect operations like searching and traversal?
Deque Data Structure with Two-Way Data Access
- A deque (double-ended queue) is a records structure that lets in insertion and deletion at both ends.
- Two-way records get entry to a method that factors can be accessed and manipulated from the front and the rear.
- Operations encompass push and pop at each end, imparting flexibility in enforcing various algorithms.
Effect of Left Child in a Tree Structure on Searching and Traversal
- The presence of a left child in a tree shape influences the sequence of operations like looking and postorder traversal, especially in binary timber.
- During an in-order traversal (left-root-right), the left infant is visited earlier than the foundation and its right toddler.
- In a binary seek tree (BST), the left baby normally holds values smaller than the determined node, affecting the traversal order.
- Searching can be optimized primarily based on the binary seek assets, where values within the left subtree are smaller and values within the proper subtree are larger.
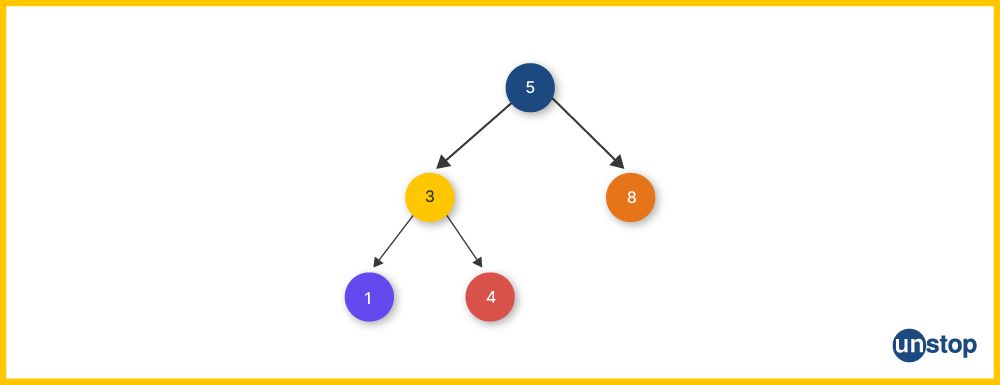
The image shows,
- In-order traversal: 1, 3, 4, five, eight.
- Searching for a fee follows the binary seek belongings, utilizing the left infant to navigate effectively.
49. Discuss the significance of memory utilization in the context of static data structures. How does the use of contiguous memory locations impact the efficiency of linear data structures compared to dynamic structures with scattered memory locations?
Memory utilization is crucial in static data structures, like arrays, because they use contiguous memory locations. This contiguity allows for:
-
Efficient Access: Elements can be accessed quickly using indexing, with O(1) time complexity, as the single memory address of any element can be calculated directly.
-
Cache Efficiency: Contiguous memory improves cache performance, as accessing one element often loads adjacent elements into the cache, speeding up subsequent accesses.
In contrast, dynamic structures like linked lists, which use scattered memory locations, have elements stored at non-contiguous addresses. This can lead to:
-
Slower Access: Accessing elements requires traversal from one node to another, resulting in O(n) time complexity for searching.
-
Cache Inefficiency: Scattered locations lead to poorer cache performance, as elements are not likely to be loaded together into the cache.
Thus, while static structures offer better memory and access efficiency, they lack the flexibility of dynamic structures in handling variable-sized data and frequent insertions or deletions.
50. Explain the role of a binary search tree in organizing data.
The primary role of a binary search tree in organizing data is as follows:
-
Ordered Structure: In a BST, each node has at most two children. The left child node contains values that are less than its parent node, while the right child node contains values that are greater. This property helps maintain an ordered structure.
-
Efficient Searching: Due to the ordering property, searching for a value can be done quickly. Starting from the root node, you can decide whether to move to the left or right child based on the comparison of the target value with the current node’s value.
-
Dynamic Operations: BSTs support dynamic data operations. You can insert and delete nodes while maintaining the ordering property, which ensures that searching remains efficient even as the tree grows or shrinks.
-
Sorted Data: Performing an in-order traversal (left subtree, root, right subtree) of a BST produces a sorted sequence of node values. This makes it easy to retrieve data in a sorted manner.
51. How does the binary search method work within the context of a binary search tree?
Binary search in the context of a BST leverages the tree’s ordering properties to quickly locate a value:
-
Start at the Root: Begin the search at the root node of the BST.
-
Compare Values:
- If the target value is equal to the value of the current node, you’ve found the target.
- If the target value is less than the value of the current node, move to the left child node.
- If the target value is greater than the value of the current node, move to the right child node.
-
Continue the Search: Repeat the comparison and movement process with the next node (left or right child) until you either find the target value or reach a leaf node (a single node with no children), indicating that the target value is not in the tree.
A self-balancing binary search tree (BST) is a type of binary tree that is used to organize and manage data in a way that facilitates efficient searching, insertion, and deletion operations. The BST has a specific structure that makes it particularly useful for dynamic sets of data where quick access to elements is required.
52. How do you find the maximum subarray sum using divide and conquer?
To find the maximum subarray sum using the divide and conquer approach, we can break down the problem into smaller subproblems, solve them independently, and then combine the results. The key idea is to recursively divide the array into two halves, solve for each half, and also consider the maximum subarray that spans the boundary between the two halves.
Here’s a step-by-step explanation and implementation of this approach:
- Divide: Split the input array into two halves.
- Conquer:
- Recursively find the maximum subarray sum in the left half.
- Recursively find the maximum subarray sum in the right half.
- Find the maximum subarray sum that crosses the middle element.
- Combine: The maximum subarray sum for the whole array is the maximum of the three values computed above.
Code:
public class MaxSubarraySum {
// Function to find the maximum subarray sum using divide and conquer
public static int maxSubarraySum(int[] array) {
return maxSubarraySum(array, 0, array.length - 1);
}
// Recursive function to find the maximum subarray sum within a range
private static int maxSubarraySum(int[] array, int left, int right) {
if (left == right) {
// Base case: only one element
return array[left];
}
int mid = (left + right) / 2;
// Find the maximum subarray sum in the left half
int leftMax = maxSubarraySum(array, left, mid);
// Find the maximum subarray sum in the right half
int rightMax = maxSubarraySum(array, mid + 1, right);
// Find the maximum subarray sum that crosses the midpoint
int crossMax = maxCrossingSubarray(array, left, mid, right);
// Return the maximum of the three values
return Math.max(leftMax, Math.max(rightMax, crossMax));
}
// Function to find the maximum subarray sum that crosses the midpoint
private static int maxCrossingSubarray(int[] array, int left, int mid, int right) {
int leftSum = Integer.MIN_VALUE;
int rightSum = Integer.MIN_VALUE;
// Calculate maximum sum of subarray ending at mid
int sum = 0;
for (int i = mid; i >= left; i--) {
sum += array[i];
if (sum > leftSum) {
leftSum = sum;
}
}
// Calculate maximum sum of subarray starting at mid + 1
sum = 0;
for (int i = mid + 1; i <= right; i++) {
sum += array[i];
if (sum > rightSum) {
rightSum = sum;
}
}
// Return the sum of the maximum subarray that crosses the midpoint
return leftSum + rightSum;
}
public static void main(String[] args) {
int[] array = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
int result = maxSubarraySum(array);
System.out.println("Maximum Subarray Sum: " + result);
}
}
cHVibGljIGNsYXNzIE1heFN1YmFycmF5U3VtIHsKCi8vIEZ1bmN0aW9uIHRvIGZpbmQgdGhlIG1heGltdW0gc3ViYXJyYXkgc3VtIHVzaW5nIGRpdmlkZSBhbmQgY29ucXVlcgpwdWJsaWMgc3RhdGljIGludCBtYXhTdWJhcnJheVN1bShpbnRbXSBhcnJheSkgewpyZXR1cm4gbWF4U3ViYXJyYXlTdW0oYXJyYXksIDAsIGFycmF5Lmxlbmd0aCAtIDEpOwp9CgovLyBSZWN1cnNpdmUgZnVuY3Rpb24gdG8gZmluZCB0aGUgbWF4aW11bSBzdWJhcnJheSBzdW0gd2l0aGluIGEgcmFuZ2UKcHJpdmF0ZSBzdGF0aWMgaW50IG1heFN1YmFycmF5U3VtKGludFtdIGFycmF5LCBpbnQgbGVmdCwgaW50IHJpZ2h0KSB7CmlmIChsZWZ0ID09IHJpZ2h0KSB7Ci8vIEJhc2UgY2FzZTogb25seSBvbmUgZWxlbWVudApyZXR1cm4gYXJyYXlbbGVmdF07Cn0KCmludCBtaWQgPSAobGVmdCArIHJpZ2h0KSAvIDI7CgovLyBGaW5kIHRoZSBtYXhpbXVtIHN1YmFycmF5IHN1bSBpbiB0aGUgbGVmdCBoYWxmCmludCBsZWZ0TWF4ID0gbWF4U3ViYXJyYXlTdW0oYXJyYXksIGxlZnQsIG1pZCk7Ci8vIEZpbmQgdGhlIG1heGltdW0gc3ViYXJyYXkgc3VtIGluIHRoZSByaWdodCBoYWxmCmludCByaWdodE1heCA9IG1heFN1YmFycmF5U3VtKGFycmF5LCBtaWQgKyAxLCByaWdodCk7Ci8vIEZpbmQgdGhlIG1heGltdW0gc3ViYXJyYXkgc3VtIHRoYXQgY3Jvc3NlcyB0aGUgbWlkcG9pbnQKaW50IGNyb3NzTWF4ID0gbWF4Q3Jvc3NpbmdTdWJhcnJheShhcnJheSwgbGVmdCwgbWlkLCByaWdodCk7CgovLyBSZXR1cm4gdGhlIG1heGltdW0gb2YgdGhlIHRocmVlIHZhbHVlcwpyZXR1cm4gTWF0aC5tYXgobGVmdE1heCwgTWF0aC5tYXgocmlnaHRNYXgsIGNyb3NzTWF4KSk7Cn0KCi8vIEZ1bmN0aW9uIHRvIGZpbmQgdGhlIG1heGltdW0gc3ViYXJyYXkgc3VtIHRoYXQgY3Jvc3NlcyB0aGUgbWlkcG9pbnQKcHJpdmF0ZSBzdGF0aWMgaW50IG1heENyb3NzaW5nU3ViYXJyYXkoaW50W10gYXJyYXksIGludCBsZWZ0LCBpbnQgbWlkLCBpbnQgcmlnaHQpIHsKaW50IGxlZnRTdW0gPSBJbnRlZ2VyLk1JTl9WQUxVRTsKaW50IHJpZ2h0U3VtID0gSW50ZWdlci5NSU5fVkFMVUU7CgovLyBDYWxjdWxhdGUgbWF4aW11bSBzdW0gb2Ygc3ViYXJyYXkgZW5kaW5nIGF0IG1pZAppbnQgc3VtID0gMDsKZm9yIChpbnQgaSA9IG1pZDsgaSA+PSBsZWZ0OyBpLS0pIHsKc3VtICs9IGFycmF5W2ldOwppZiAoc3VtID4gbGVmdFN1bSkgewpsZWZ0U3VtID0gc3VtOwp9Cn0KCi8vIENhbGN1bGF0ZSBtYXhpbXVtIHN1bSBvZiBzdWJhcnJheSBzdGFydGluZyBhdCBtaWQgKyAxCnN1bSA9IDA7CmZvciAoaW50IGkgPSBtaWQgKyAxOyBpIDw9IHJpZ2h0OyBpKyspIHsKc3VtICs9IGFycmF5W2ldOwppZiAoc3VtID4gcmlnaHRTdW0pIHsKcmlnaHRTdW0gPSBzdW07Cn0KfQoKLy8gUmV0dXJuIHRoZSBzdW0gb2YgdGhlIG1heGltdW0gc3ViYXJyYXkgdGhhdCBjcm9zc2VzIHRoZSBtaWRwb2ludApyZXR1cm4gbGVmdFN1bSArIHJpZ2h0U3VtOwp9CgpwdWJsaWMgc3RhdGljIHZvaWQgbWFpbihTdHJpbmdbXSBhcmdzKSB7CmludFtdIGFycmF5ID0gey0yLCAxLCAtMywgNCwgLTEsIDIsIDEsIC01LCA0fTsKaW50IHJlc3VsdCA9IG1heFN1YmFycmF5U3VtKGFycmF5KTsKU3lzdGVtLm91dC5wcmludGxuKCJNYXhpbXVtIFN1YmFycmF5IFN1bTogIiArIHJlc3VsdCk7Cn0KfQ==
53. How do you implement a link-cut tree, and what are its applications?
A link-cut tree is a tree data structure used to dynamically maintain a forest (a collection of trees) under operations that involve cutting and linking trees, as well as accessing information about the paths and trees themselves. It supports several key operations efficiently, making it useful for various applications in computer science and combinatorial optimization.
The implementation of a link-cut tree data structure involves several key concepts:
-
Splay Trees: The link-cut tree uses splay trees as its underlying data structure. Splay trees are self-balancing binary search trees that allow for efficient access, insertion, and deletion operations.
-
Node Representation: Each node in the link-cut tree represents a vertex in the forest and has pointers to its parent and children, as well as a path-parent pointer used during the splay operation.
-
Key Operations:
- Access(v): This operation makes v the root of its represented tree in the forest, splaying v and its ancestors in the splay tree, effectively making the preferred path containing v accessible.
- Link(v, w): Links the tree containing v to the tree containing w by making w the parent of v. This operation requires v to be a root node.
- Cut(v): Cuts the edge between v and its parent, separating v and its subtree from the rest of the tree.
- FindRoot(v): Finds the root of the tree containing v.
- LCA(v, w): Finds the lowest common ancestor of v and w.
- Evert(v): Makes v the root of its tree, effectively inverting the path from v to the root.
Link-cut trees are useful in several scenarios where dynamic trees need to be managed efficiently:
-
Dynamic Graph Algorithms: Link-cut trees are used to dynamically maintain the structure of a graph as edges are added or removed, which is essential in algorithms for finding minimum spanning trees, dynamic connectivity, and program flow analysis problems.
-
Network Design and Analysis: In telecommunications and computer networks, link-cut trees can manage network topologies, allowing for quick adjustments to the network structure.
-
Dynamic Trees in Game Theory: Link-cut trees can be used to manage game states and transitions, especially in games involving dynamic environments or where game trees change frequently.
-
Data Structure Optimization: They are used in optimizing data structures for basic operations that involve dynamic set updates, such as maintaining sets of elements under union and find operations.
54. How do you implement a priority search tree?
A priority search tree (PST) is a data structure used to efficiently perform range queries in a 2D plane. It helps in finding all points that intersect with a given rectangular region. Here's how to implement it:
-
Data Structure: Each header node contains a point (x,y) and maintains a list of points in the rectangle where this node’s y-coordinate is the maximum.
-
Building the Tree:
- Sort Points: Sort the points by their y-coordinates in descending order.
- Root Node: Choose the point with the highest y-coordinate as the root.
- Partition: Divide the remaining points into two sets:
- Left Set: Points with x-coordinates less than the root’s x-coordinate.
- Right Set: Points with x-coordinates greater than or equal to the root’s x-coordinate.
- Recursion: Recursively build the tree for the left and right sets.
-
Searching: To find points within a query rectangle, traverse the tree:
-
- Check Node: If the query rectangle intersects with the node’s rectangle, include the node’s points in the result.
- Recursive Search: Recursively search the left and right subtrees if their rectangles intersect with the query rectangle.
-
55. Explain the concept of a suffix tree and its applications.
A suffix tree is a specialized data structure used to efficiently store and analyze all suffixes of a given string in a program. It is particularly useful for solving various string processing problems.
Structure:
- Nodes: Each separate node in a suffix tree represents a substring of the original string. Nodes can represent either single characters or longer substrings.
- Edges: Edges between single root nodes are labelled with substrings of the original string.
- Leaves: Each leaf node represents a suffix of the string, and the path from the root to the leaf encodes the suffix.
- Root: The root of the suffix tree represents the empty string.
Construction:
- Build Process: Constructing a suffix tree involves inserting all suffixes of the string into a tree. This process typically involves the use of advanced algorithms such as Ukkonen's algorithm or McCreight's algorithm to build the tree in linear time.
- Edge Labeling: The edges are labeled with substrings of the original string, and each edge label is associated with the start and end indices of the substring in the original string.
Applications:
- Substring Search: Efficiently find occurrences of substrings.
- Pattern Matching: Supports finding the longest common substring or substring occurrences.
- Data Compression: Used in algorithms for data compression, like the Burrows-Wheeler transform.
- Genome Sequencing: Helps in bioinformatics for matching DNA sequences.
56. Write a program to check if a binary tree is balanced.
A binary tree is considered balanced if the difference in height between the left and right subtrees of every node is no more than 1. The program to check if a binary tree is balanced or not is as follows:
Code:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
public class BalancedBinaryTree {
public boolean isBalanced(TreeNode root) {
return checkHeight(root) != -1;
}
private int checkHeight(TreeNode node) {
if (node == null) return 0;
int leftHeight = checkHeight(node.left);
if (leftHeight == -1) return -1;
int rightHeight = checkHeight(node.right);
if (rightHeight == -1) return -1;
if (Math.abs(leftHeight - rightHeight) > 1) return -1;
return Math.max(leftHeight, rightHeight) + 1;
}
}
Y2xhc3MgVHJlZU5vZGUgewppbnQgdmFsOwpUcmVlTm9kZSBsZWZ0OwpUcmVlTm9kZSByaWdodDsKVHJlZU5vZGUoaW50IHgpIHsgdmFsID0geDsgfQp9CgpwdWJsaWMgY2xhc3MgQmFsYW5jZWRCaW5hcnlUcmVlIHsKcHVibGljIGJvb2xlYW4gaXNCYWxhbmNlZChUcmVlTm9kZSByb290KSB7CnJldHVybiBjaGVja0hlaWdodChyb290KSAhPSAtMTsKfQoKcHJpdmF0ZSBpbnQgY2hlY2tIZWlnaHQoVHJlZU5vZGUgbm9kZSkgewppZiAobm9kZSA9PSBudWxsKSByZXR1cm4gMDsKCmludCBsZWZ0SGVpZ2h0ID0gY2hlY2tIZWlnaHQobm9kZS5sZWZ0KTsKaWYgKGxlZnRIZWlnaHQgPT0gLTEpIHJldHVybiAtMTsKCmludCByaWdodEhlaWdodCA9IGNoZWNrSGVpZ2h0KG5vZGUucmlnaHQpOwppZiAocmlnaHRIZWlnaHQgPT0gLTEpIHJldHVybiAtMTsKCmlmIChNYXRoLmFicyhsZWZ0SGVpZ2h0IC0gcmlnaHRIZWlnaHQpID4gMSkgcmV0dXJuIC0xOwoKcmV0dXJuIE1hdGgubWF4KGxlZnRIZWlnaHQsIHJpZ2h0SGVpZ2h0KSArIDE7Cn0KfQ==
Conclusion
Throughout this article, we have covered all the important and frequently asked data structures and algorithms interview questions, providing you with the knowledge and insights needed to excel in your next technical interview. With these foundational concepts and practical examples, you're well-equipped to tackle any challenges that come your way and demonstrate your proficiency in data structures.
Here are a few other topics that you might be interested in reading:
I’m a Computer Science graduate with a knack for creative ventures. Through content at Unstop, I am trying to simplify complex tech concepts and make them fun. When I’m not decoding tech jargon, you’ll find me indulging in great food and then burning it out at the gym.
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter
Blogs you need to hog!

How To Write Finance Cover Letter For Morgan Stanley (+Free Sample!)

55+ Data Structure Interview Questions For 2026 (Detailed Answers)

How To Negotiate Salary With HR: Tips And Insider Advice










Comments
Add comment