- What Is Data Structure?
- Key Features Of Data Structures
- Basic Terminologies Related To Data Structures
- Types Of Data Structures
- What Are Linear Data Structures & Its Types?
- What Are Non-Linear Data Structures & Its Types?
- Importance Of Data Structure In Programming
- Basic Operations On Data Structures
- Applications Of Data Structures
- Real-Life Applications Of Data Structures
- Linear Vs. Non-linear Data Structures
- What Are Algorithms? The Difference Between Data Structures & Algorithms
- Conclusion
- Frequently Asked Questions
- What Is Asymptotic Notation?
- How Asymptotic Notation Helps In Analyzing Performance
- Types Of Asymptotic Notation
- Big-O Notation (O)
- Omega Notation (Ω)
- Theta Notation (Θ)
- Little-O Notation (o)
- Little-Omega Notation (ω)
- Summary Of Asymptotic Notations
- Real-World Applications Of Asymptotic Notation
- Conclusion
- Frequently Asked Questions
- Understanding Big O Notation
- Types Of Time Complexity
- Space Complexity In Big O Notation
- How To Determine Big O Complexity
- Best, Worst, And Average Case Complexity
- Applications Of Big O Notation
- Conclusion
- Frequently Asked Questions
- What Is Time Complexity?
- Why Do You Need To Calculate Time Complexity?
- The Time Complexity Algorithm Cases
- Time Complexity: Different Types Of Asymptotic Notations
- How To Calculate Time Complexity?
- Time Complexity Of Sorting Algorithms
- Time Complexity Of Searching Algorithms
- Writing And optimizing An algorithm
- What Is Space Complexity And Its Significance?
- Relation Between Time And Space Complexity
- Conclusion
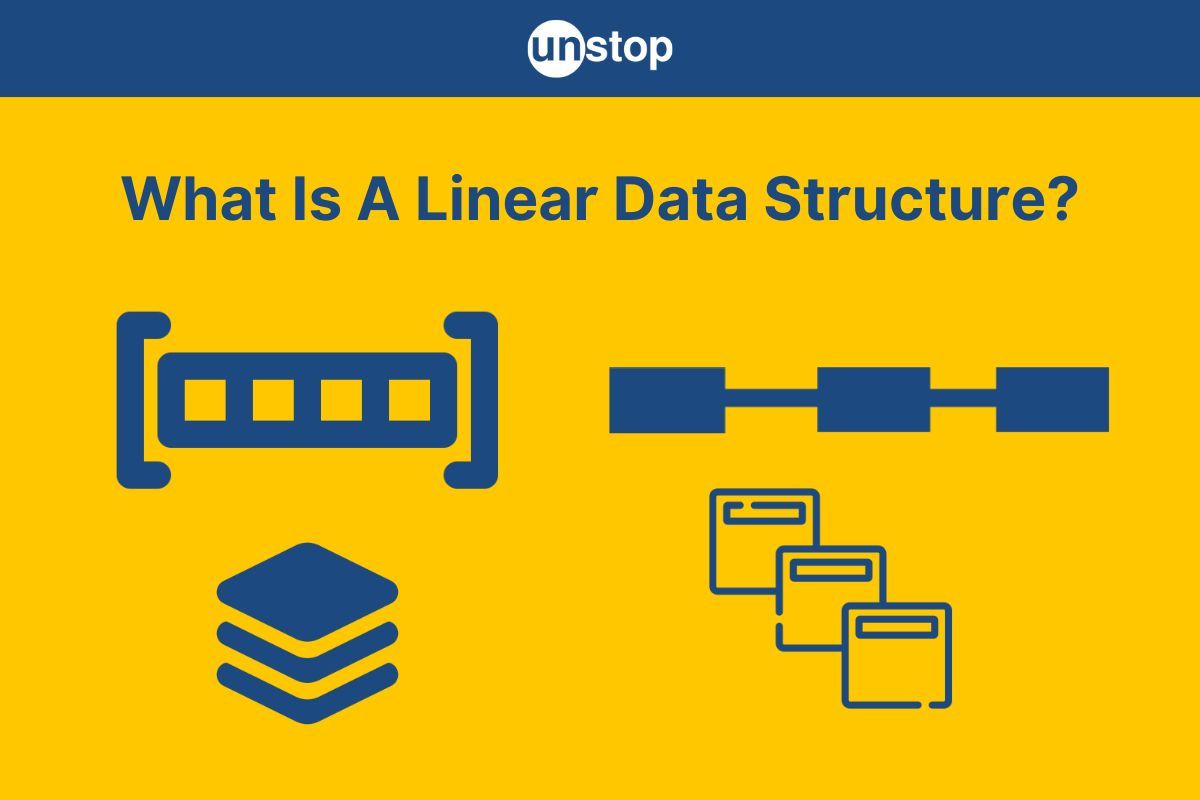
- What Is Linear Data Structure?
- Key Characteristics Of Linear Data Structures
- What Are The Types Of Linear Data Structures?
- What Is An Array Linear Data Structure?
- What Are Linked Lists Linear Data Structure?
- What Is A Stack Linear Data Structure?
- What Is A Queue Linear Data Structure?
- Most Common Operations Performed in Linear Data Structures
- Advantages Of Linear Data Structures
- What Is Nonlinear Data Structure?
- Difference Between Linear & Non-Linear Data Structures
- Who Uses Linear Data Structures?
- Conclusion
- Frequently Asked Questions
- What is a linear data structure?
- What is a non-linear data structure?
- Difference between linear data structure and non-linear data structure
- FAQs about linear and non-linear data structures
- What Is Search?
- What Is Linear Search In Data Structure?
- What Is Linear Search Algorithm?
- Working Of Linear Search Algorithm
- Complexity Of Linear Search Algorithm In Data Structures
- Implementations Of Linear Search Algorithm In Different Programming Languages
- Real-World Applications Of Linear Search In Data Structure
- Advantages & Disadvantages Of Linear Search
- Best Practices For Using Linear Search Algorithm
- Conclusion
- Frequently Asked Questions
- What Is The Binary Search Algorithm?
- Conditions For Using Binary Search
- Steps For Implementing Binary Search
- Iterative Method For Binary Search With Implementation Examples
- Recursive Method For Binary Search
- Complexity Analysis Of Binary Search Algorithm
- Iterative Vs. Recursive Implementation Of Binary Search
- Advantages & Disadvantages Of Binary Search
- Practical Applications & Real-World Examples Of Binary Search
- Conclusion
- Frequently Asked Questions
- Understanding The Jump Search Algorithm
- How Jump Search Works?
- Code Implementation Of Jump Search Algorithm
- Time And Space Complexity Analysis
- Advantages Of Jump Search
- Disadvantages Of Jump Search
- Applications Of Jump Search
- Conclusion
- Frequently Asked Questions
- What Is Sorting In Data Structures?
- What Is Bubble Sort?
- What Is Selection Sort?
- What Is Insertion Sort?
- What Is Merge Sort?
- What Is Quick Sort?
- What Is Heap Sort?
- What Is Radix Sort?
- What Is Bucket Sort?
- What Is Counting Sort?
- What Is Shell Sort?
- Choosing The Right Sorting Algorithm
- Applications Of Sorting
- Conclusion
- Frequently Asked Questions
- Understanding Bubble Sort Algorithm
- Bubble Sort Algorithm
- Implementation Of Bubble Sort In C++
- Time And Space Complexity Analysis Of Bubble Sort Algorithm
- Advantages Of Bubble Sort Algorithm
- Disadvantages Of Bubble Sort Algorithm
- Applications of Bubble Sort Algorithms
- Conclusion
- Frequently Asked Questions
- Understanding The Merge Sort Algorithm
- Algorithm For Merge Sort
- Implementation Of Merge Sort In C++
- Time And Space Complexity Analysis Of Merge Sort
- Advantages And Disadvantages Of Merge Sort
- Applications Of Merge Sort
- Conclusion
- Frequently Asked Questions
- Understanding The Selection Sort Algorithm
- Algorithmic Approach To Selection Sort
- Implementation Of Selection Sort Algorithm
- Complexity Analysis Of Selection Sort
- Comparison Of Selection Sort With Other Sorting Algorithms
- Advantages And Disadvantages Of Selection Sort
- Application Of Selection Sort
- Conclusion
- Frequently Asked Questions
- What Is Insertion Sort Algorithm?
- How Does Insertion Sort Work? (Step-by-Step Explanation)
- Implementation of Insertion Sort in C++
- Time And Space Complexity Of Insertion Sort
- Applications Of Insertion Sort Algorithm
- Comparison With Other Sorting Algorithms
- Conclusion
- Frequently Asked Questions
- Understanding Quick Sort Algorithm
- Step-By-Step Working Of Quick Sort
- Implementation Of Quick Sort Algorithm
- Time Complexity Analysis Of Quick Sort
- Advantages Of Quick Sort Algorithm
- Disadvantages Of Quick Sort Algorithm
- Applications Of Quick Sort Algorithm
- Conclusion
- Frequently Asked Questions
- Understanding The Heap Data Structure
- Working Of Heap Sort Algorithm
- Implementation Of Heap Sort Algorithm
- Advantages Of Heap Sort
- Disadvantages Of Heap Sort
- Real-World Applications Of Heap Sort
- Conclusion
- Frequently Asked Questions
- Understanding The Counting Sort Algorithm
- Conditions For Using Counting Sort Algorithm
- How Counting Sort Algorithm Works?
- Implementation Of Counting Sort Algorithm
- Time And Space Complexity Analysis Of Counting Sort
- Comparison Of Counting Sort With Other Sorting Algorithms
- Advantages Of Counting Sort Algorithm
- Disadvantages Of Counting Sort Algorithm
- Applications Of Counting Sort Algorithm
- Conclusion
- Frequently Asked Questions
- Understanding Shell Sort Algorithm
- Working Of Shell Sort Algorithm
- Implementation Of Shell Sort Algorithm
- Time Complexity Analysis Of Shell Sort Algorithm
- Advantages Of Shell Sort Algorithm
- Disadvantages Of Shell Sort Algorithm
- Applications Of Shell Sort Algorithm
- Conclusion
- Frequently Asked Questions
- What Is Linked List In Data Structures?
- Types Of Linked Lists In Data Structures
- Linked List Operations In Data Structures
- Advantages And Disadvantages Of Linked Lists In Data Structures
- Comparison Of Linked Lists And Arrays
- Applications Of Linked Lists
- Conclusion
- Frequently Asked Questions
- What Is A Singly Linked List In Data Structure?
- Insertion Operations On Singly Linked Lists
- Deletion Operation On Singly Linked List
- Searching For Elements In Single Linked List
- Calculating Length Of Single Linked List
- Practical Applications Of Singly Linked Lists In Data Structure
- Common Problems With Singly Linked Lists
- Conclusion
- Frequently Asked Questions (FAQ)
- What Is A Linked List?
- Reverse A Linked List
- How To Reverse A Linked List? (Approaches)
- Recursive Approach To Reverse A Linked List
- Iterative Approach To Reverse A Linked List
- Using Stack To Reverse A Linked List
- Complexity Analysis Of Different Approaches To Reverse A Linked List
- Conclusion
- Frequently Asked Questions
- What Is A Stack In Data Structure?
- Understanding Stack Operations
- Stack Implementation In Data Structures
- Stack Implementation Using Arrays
- Stack Implementation Using Linked Lists
- Comparison: Array vs. Linked List Implementation
- Applications Of Stack In Data Structures
- Advantages And Disadvantages Of Stack Data Structure
- Conclusion
- Frequently Asked Questions
- What Is A Graph Data Structure?
- Importance Of Graph Data Structures
- Types Of Graphs In Data Structure
- Types Of Graph Algorithms
- Application Of Graphs In Data Structures
- Challenges And Complexities In Graphs
- Conclusion
- Frequently Asked Questions
- What Is Tree Data Structure?
- Terminologies Of Tree Data Structure:
- Different Types Of Tree Data Structures
- Basic Operations On Tree Data Structure
- Applications Of Tree Data Structures
- Comparison Of Trees, Graphs, And Linear Data Structures
- Advantages Of Tree Data Structure
- Disadvantages Of Tree Data Structure
- Conclusion
- Frequently Asked Questions
- What Is Dynamic Programming?
- Real-Life Example: The Jigsaw Puzzle Analogy
- How To Solve A Problem Using Dynamic Programming?
- Dynamic Programming Algorithm Techniques
- Advantages Of Dynamic Programming
- Disadvantages Of Dynamic Programming
- Applications Of Dynamic Programming
- Conclusion
- Frequently Asked Questions
- Understanding The Sliding Window Algorithm
- How Does The Sliding Window Algorithm Works?
- How To Identify Sliding Window Problems?
- Fixed-Size Sliding Window Example: Maximum Sum Subarray Of Size k
- Variable-Size Sliding Window Example: Smallest Subarray With A Given Sum
- Advantages Of Sliding Window Technique
- Disadvantages Of Sliding Window Technique
- Conclusion
- Frequently Asked Questions
- Introduction To Data Structures
- Data Structures Interview Questions: Basics
- Data Structures Interview Questions: Intermediate
- Data Structures Interview Questions: Advanced
- Conclusion
What Is Linear Data Structure? Types, Uses & More (+ Examples)
Data structures, a fundamental concept in computer science, are essential for organizing and managing data efficiently. They help optimise data access and manipulation, making them crucial for effective algorithm implementation. In this article, we will explore what is linear data structure, its types, some fundamental operations, and more.
What Is Data Structure?
A data structure is a specialized format for organizing, processing, and storing data. It defines the relationship between data elements, facilitating efficient data management and access. Data structures are foundational to designing efficient algorithms and enhancing software performance.
What Is Linear Data Structure?
A linear data structure is a type of data structure where elements are arranged in a sequential order, one after the other. Each element is connected to its previous and next element, forming a linear sequence. This arrangement allows for straightforward traversal, insertion, and deletion operations.
- Linear data structures are essential in as they provide a simple and efficient way to store and access data.
- They are used in various algorithms and applications, ranging from simple data storage to complex problem-solving techniques.
- Examples of linear data structures include arrays, linked lists, stacks, and queues. Each of these structures has its unique properties and use cases, but they all share the common trait of linear organization.
- In contrast, nonlinear data structures are those that do not arrange data sequentially but rather in a hierarchical or interconnected manner. Some examples are trees (binary trees, etc.) and graphs.
All in all, linear data structures help arrange data in a sequential manner, making it easier to traverse and manage. Understanding linear data structures is fundamental as they form the building blocks for more complex structures and algorithms.
Key Characteristics Of Linear Data Structures
Linear data structures have several defining characteristics that make them integral to data organization and algorithm efficiency. Some of the key characteristics include:
- Sequential Arrangement: Elements are arranged in a linear sequence, with each element connected to its previous and next element.
- Single-Level Data Storage: The data elements are stored at a single level, unlike hierarchical structures such as trees.
- Easy & Efficient Traversal: Traversing through elements is straightforward, typically requiring a single loop or iteration.
- Efficient Memory Usage: Linear data structures are memory-efficient for storage, often requiring contiguous memory locations.
- Insertion and Deletion Operations: Operations such as insertion and deletion can be performed with relative ease, especially in structures like linked lists.
- Fixed Size or Dynamic: Some linear structures, like arrays, have a fixed size, while others, like linked lists, can dynamically grow or shrink.
These characteristics make linear data structures fundamental for various applications, providing a simple yet powerful means to manage and manipulate data.
What Are The Types Of Linear Data Structures?
Linear data structures come in various forms, each with unique characteristics and use cases. Some of the most common types include:
- Arrays: A collection of elements stored in contiguous/ adjacent memory locations, where elements are identified by index or key. Arrays have a fixed size and allow for efficient random access.
- Linked Lists: A sequence of elements called nodes, i.e., a collection of nodes. Each current node contains a data element and a reference (i.e., a link or connection between nodes) to the next node in the sequence. Linked lists can grow or shrink dynamically.
- Stacks: A linear data structure that follows the Last In, First Out (LIFO) principle, where the most recently added element is the first to be removed. Stacks are commonly used in recursion and backtracking algorithms.
- Queues: A linear data structure that follows the First In, First Out (FIFO) principle, where the earliest added element is the first to be removed. Queues are useful for managing tasks in sequential order.
These linear data structures are fundamental to many programming algorithms and applications. Each type of structure serves specific purposes in data management and processing. We will discuss each of these in detail in the sections ahead.
What Is An Array Linear Data Structure?
An array is a linear data structure that stores a collection of elements, typically of the same data type, in contiguous memory locations.
- They are created using the square bracket notation in most languages, where the brackets contain the dimensions or the elements.
- Each element in the array can be accessed using an index, making it easy to retrieve and manipulate data.
Arrays are widely used due to their simplicity and efficiency in accessing elements.
Key Characteristics Of Array Linear Data Structure
Array is one of the most common data structure with wide applications in programming. Some important characteristics of this linear data structure type are:
- Fixed Size: Once an array is declared, its size cannot be changed.
- Index-Based Access: Elements can be accessed directly using their index.
- Homogeneous Elements: All elements in the array are of the same data type.
- Contiguous Memory Allocation: Elements are stored in consecutive memory locations.
Types Of Arrays Linear Data Structures
There are three common types of arrays in programming, including:
1. One-Dimensional Array: A single row of elements, also known as a linear array. For example-
int[] numbers = {1, 2, 3, 4, 5};
2. Two-Dimensional Array: An array of arrays often used to represent matrices or tables.
int[][] matrix = {{1, 2}, {3, 4}};
3. Multi-Dimensional Array: Arrays with more than two dimensions are used for complex data representations. For example:
int[][][] threeD = {{{1, 2}, {3, 4}}, {{5, 6}, {7, 8}}};
Operations On Array Linear Data Structures
The most common operation performed on an array is the simple traversal of an entire array to access, update or modify its elements. Other operations include:
1. Accessing an Element: Accessing an element in an array retrieves the value stored at a specific index. Loops allow for efficient traversal and efficient indexing of elements, which is why the complexity for element access is usually O(1), i.e., constant time complexity.
2. Inserting an Element: This involves adding an element/ a new value at a specified index or at the end of the array. The complexity for element insertion varies as follows-
- At the End (Appending): O(1) on average, O(n) in the worst case. Appending to the end requires checking and potentially resizing the array.
- At a Specific Index (Insertion): O(n). Insertion at arbitrary positions requires shifting subsequent elements.
3. Deleting/ Removal Of Element: Deleting an element removes a value from a specified index or from the end of the array. The complexity of this operation depends on where the element is being removed from. That is-
- From the End: O(1) on average, O(n) in worst case. Deleting the last element is straightforward.
- From a Specific Index: O(n). Deleting an element involves shifting subsequent elements to close the gap.
4. Searching for an Element (Linear Search): Searching finds the index of a specified value in the array, if present. The complexity for the linear search operation generally remains O(n) - Linear time. In the worst case, the search may need to examine every element in the array.
5. Sorting the Array (Using Efficient Sorting Algorithms): Sorting arranges the elements in either ascending or descending order. The best and worst case complexity for this operation is-
- Best Sorting Algorithms (e.g., QuickSort, MergeSort): O(n log n). Efficient sorting algorithms minimize comparisons and swaps.
- Worst Case (e.g., BubbleSort, SelectionSort): O(n^2). Less efficient algorithms perform poorly on large datasets.
6. Updating an Element: Updating modifies the value of an existing element at a specified index. The complexity for this operation is O(1) - Constant time. Updating an element by index is a direct operation.
Advantages & Disadvantages Of Array Linear Data Structures
The table below lists the key advantages and disadvantages of array linear data structures.
| Advantages | Disadvantages |
|
|
Also Read: Advantages And Disadvantages Of Array In Programming
What Are Linked Lists Linear Data Structure?
As mentioned before, a linked list is a linear data structure consisting of nodes where each node contains a data element and a reference (or link) to the next node in the sequence.
- Unlike arrays, linked lists do not store elements in contiguous memory locations. Instead, each element points to the next element, forming a chain-like structure of connected memory locations.
- This dynamic arrangement allows for efficient insertion and deletion operations.
Linked lists are particularly useful when the number of elements is unknown or when frequent insertions and deletions are required.
Key Characteristics Of Linked List Linear Data Structure
- Dynamic Size: Linked lists can grow or shrink in size dynamically, making them more flexible than arrays.
- Non-Contiguous Memory Allocation: Nodes are not stored in contiguous memory locations, allowing for efficient usage and allocation of memory.
- Node-Based Structure: Each node contains a data element and a reference (or pointer) to the next node.
- Ease of Insertion/Deletion: Adding or removing nodes is relatively simple and efficient, especially compared to arrays.
Types of Linked List Linear Data Structure
- Singly Linked List: Each node contains a single reference to the next node in the sequence. Example:
Node1 -> Node2 -> Node3 -> NULL
- Doubly Linked List: Each node contains two references: one to the next node and one to the previous node, allowing for bidirectional traversal. Example:
NULL <- Node1 <-> Node2 <-> Node3 -> NULL
- Circular Linked List: The last node of the list points back to the first node, forming a circular structure. Example:
Node1 -> Node2 -> Node3 -> Node1 (and so on)
Common Operations On Linked List Linear Data Structure
Some common operations on the linked list linear data structure types include:
1. Accessing an Element: Accessing an element in a linked list involves traversing from the head (or tail in doubly linked lists) to the desired position. The complexity for common traversal methods on linked lists is O(n) - Linear time. Accessing an element requires traversing through the list until reaching the desired node.
2. Inserting an Element: Inserting an element in a linked list typically involves creating a new node and adjusting pointers to link it correctly within the list. The complexity for element insertion in linked list linear data structure varies as follows-
- At the Beginning: O(1) - Constant time complexity. Insertion at the head of the linked list involves updating the head pointer.
- At the End: O(n) in the worst case. Insertion at the end requires traversing the entire list to reach the last node.
- At a Specific Position: O(n). Insertion at an arbitrary position involves traversing to the insertion point and adjusting pointers.
3. Deleting an Element: Deleting an element from a linked list involves adjusting pointers to bypass the node to be deleted and freeing its memory. The complexity for element deletion is-
- From the Beginning: O(1) - Constant time. Deleting the head node involves updating the head pointer.
- From the End: O(n) in the worst case. Deleting the last node requires traversing the entire list to reach the second last node.
- From a Specific Position: O(n). Deleting a node at an arbitrary position involves traversing to the deletion point and adjusting pointers.
4. Searching for an Element: Searching for an element in a linked list involves traversing the list from the head (or tail) and comparing each node's value until finding the desired element. O(n) - Linear time. In the worst case, searching may require traversing through all nodes in the list.
5. Sorting the Linked List: Sorting a linked list rearranges its elements in ascending or descending order based on their values.
- Efficient Sorting Algorithms (e.g., MergeSort): O(n log n). Efficient algorithms minimize comparisons and swaps.
- Less Efficient Algorithms (e.g., BubbleSort): O(n^2). Less efficient algorithms may perform poorly on large lists.
6. Updating an Element: Updating an element in a linked list involves traversing to the node to be updated and modifying its value. The complexity for element updations is O(n), i.e., linear time, as updating requires traversing through the list until reaching the desired node.
7. Merging Linked Lists: Merging two linked lists combines their elements into a single linked list while preserving their order. Since merging requires iterating through both lists to link them into a single list, the complexity is- O(n), i.e., linear time.
8. Reversing the Linked List: Reversing a linked list changes the order of its elements by reversing the pointers between nodes. Reversing involves iterating through the list once and adjusting pointers to reverse the order of nodes, so the complexity is linear time, i.e., O(n).
Advantages & Disadvantages Of Linked List Linear Data Structures
| Advantages | Disadvantages |
|
|
Also Read: Advantages And Disadvantages Of Linked Lists Summed Up For You
What Is A Stack Linear Data Structure?
A stack is a linear data structure that follows the Last In, First Out (LIFO) principle. As the name suggests, the elements are stacked one after another.
- This means that the last element added to the stack is the first one to be removed.
- Stacks are used in a variety of applications, including function call management in programming, expression evaluation, and syntax parsing.
They can be implemented using arrays or linked lists, providing a simple yet powerful way to manage data.
Key Features Of Stack Linear Data Structures
- LIFO Principle: The Last In, First Out principle ensures that the most recently added element is the first to be removed.
- Dynamic Size: Stacks can dynamically grow and shrink as elements are added or removed.
- Single Entry/Exit Point: All operations (push, pop, peek) are performed from one end of the stack, known as the top.
- Efficient Operations: Insertion (push) and deletion (pop) operations are performed in constant time, O(1).
Types Of Stack Linear Data Structures
- Static Stack: Implemented using arrays with a fixed size. The size of the stack is determined at compile time. For example:
int stack[10];
- Dynamic Stack: Implemented using linked lists, allowing the stack to grow and shrink dynamically without a predefined limit. For example, a linked list can be used to manage stack nodes.
- Double-Ended Stack (Deque): Allows insertion and deletion of elements from both ends, although this is less common for typical stack use cases. For example (in C++):
std::deque
Common Operations On Stack Linear Data Structures
Here are some of the most popular data structure operations for stacks:
-
Push(): This operation refers to pushing (or adding) an element onto the stack, specifically pushing a new/ additional element on top of the stack. This operation usually has a constant time complexity of O(1), as pushing an element onto a stack is a direct operation. Example:
stack.push(10);
-
Pop(): The pop operation refers to popping (or removing) an element from the stack, specifically removing the topmost element. It also has a constant time complexity, i.e., O(1), as popping an element from a stack is also a direct operation. Example:
int topElement = stack.pop();
-
Peeking at the Top Element: Peeking allows you to view the top element of the stack without removing it. The complexity of this popular data structure operation is also O(1), i.e., constant time as peeking accesses the top element directly. Example:
int topElement = stack.peek();
-
Checking if the Stack is Empty: Checking if the stack is empty verifies whether there are any elements present in the stack. It has constant time complexity- O(1) as checking the emptiness of a stack is a direct operation. Example:
bool isEmpty = stack.isEmpty();
- Searching for an Element: Searching for an element in a stack involves iterating through the stack elements to find a specific value. This operation has a linear time complexity, i.e., O(n), as in the worst case, searching may require traversing through all elements in the stack.
- Sorting the Stack: Sorting a stack arranges its elements in either ascending or descending order. The complexity of this operation is-
- Efficient Sorting Algorithms (e.g., MergeSort for Stacks): O(n log n). Efficient algorithms minimize comparisons and swaps.
- Less Efficient Algorithms (e.g., BubbleSort for Stacks): O(n^2). Less efficient algorithms may perform poorly on large stacks.
-
Reversing the Stack: Reversing a stack changes the order of its elements, typically achieved using an auxiliary stack. This operation has linear time complexity O(n), as reversing involves pushing elements into a new stack and popping them back to reverse the order.
These operations exemplify the stack's Last In, First Out (LIFO) principle, where elements are added and removed from the same end. Understanding their complexities is crucial for designing efficient algorithms that utilize stack data structures effectively in various applications.
Advantages & Disadvantages Of Stack Linear Data Structures
| Advantages | Disadvantages |
|
|
What Is A Queue Linear Data Structure?
A queue is a linear data structure that follows the First In, First Out (FIFO) principle in contrast to stacks. That is, in queues the first element added to the queue is the first to be removed. This structure is analogous to a real-life queue, such as a line of people waiting for a service, where the first person in line is served first. Queues are widely used in various applications, including task scheduling, buffering, and breadth-first search algorithms.
Key Features Of Queue Linear Data Structure
- FIFO Principle: The First In, First Out (FIFO) principle ensures that the first element added is the first to be removed.
- Two Ends: Operations are performed at two different ends; insertion (enqueue) at the rear and deletion (dequeue) at the front.
- Dynamic Size: Queues can dynamically grow and shrink as elements are added or removed.
- Ordered Structure: Elements maintain the order in which they are added, ensuring predictable access patterns.
Types Of Queue Linear Data Structure
- Simple Queue: Also known as a linear queue, where elements are added at the rear and removed from the front. For example:
int queue[SIZE];
- Circular Queue: A queue that treats the array as circular, connecting the end back to the front and making efficient use of space. Example:
if (rear == SIZE - 1) rear = 0; else rear++;
- Priority Queue: Elements are added with priority, and the element with the highest priority is removed first, regardless of the order of insertion. Example:
enqueue(element, priority);
- Deque (Double-Ended Queue): A queue where elements can be added or removed from both the front and the rear. Example:
deque.push_front(element); deque.push_back(element);
Operations On Queue Linear Data Structure
Here is a list of the operations that are most commonly performed on the queue linear data structure type:
-
Enqueue: It entails adding a new element to the rear of the queue. The complexity for element insertion in the queue is O(1), i.e., constant time as an enqueue operation directly adds an element to the rear of the queue. Example:
queue.enqueue(element);
-
Dequeue: In keeping with the FIFO principle, this operation entails removing the front element from the queue. It has constant time complexity, i.e., O(1), since the dequeue operation directly removes the front element from the queue. Example:
queue.dequeue();
-
Front: This operation returns the front element without removing it from the queue. It has a complexity of O(1), i.e., constant time, since the operation retrieves the front element without altering the queue. Example:
element = queue.front();
-
Rear: Returns the rear element without removing it from the queue and has a constant time complexity, i.e., O(1). Example:
element = queue.rear();
-
IsEmpty: Checks if the queue is empty using the isEmpty() method. It returns a boolean value and has a constant time complexity of O(1). Example:
bool isEmpty = queue.isEmpty();
-
Size: This operation returns the number of elements in the queue and has a complexity O(1), i.e., constant time. Example:
int size = queue.size();
Understanding the complexities of these operations is crucial for designing efficient algorithms and applications that utilize queue data structures effectively in various scenarios.
Advantages & Disadvantages Of Queue Linear Data Structures
| Advantages | Disadvantages |
|
|
Most Common Operations Performed in Linear Data Structures
As seen in the sections above, linear data structures (arrays, linked lists, stacks, and queues), support a variety of operations for manipulation and modification of the data they contain. Let's compile the most common operations:
1. Traversal:
This is the process of accessing and processing each element of the data structure sequentially. This operation is essential for performing tasks like searching, updating, or displaying the elements.
2. Insertion:
This process refers to adding a new element to the linear data structure at a specified position. This involves shifting existing elements to make space for the new element. The syntax for insertion varies depending on the data structure and language, typically using an indexing operator [] for arrays.
3. Deletion of Elements:
Deletion involves removing an element from the data structure at a specified position. This requires shifting the subsequent elements to fill the gap left by the removed element.
4. Searching:
Searching involves finding the position of an element within the data structure. This can be done using linear or binary search algorithms, depending on whether the data is sorted.
5. Sorting:
Sorting refers to the process of arranging the data structure elements in a specific order, either ascending or descending. Various algorithms like bubble sort, quicksort, mergesort, insertion sort, etc., can be used, each with different syntax and performance characteristics.
6. Merging:
Merging combines two data structures into one, preserving the order of elements. This operation is often used in conjunction with sorting to merge sorted lists or arrays efficiently.
7. Reversing:
Reversing changes the order of elements in the data structure, making the last element the first and vice versa. This operation is useful in various algorithms and applications where the order of data needs to be inverted.
These operations are fundamental for manipulating linear data structures efficiently, providing a solid foundation for more complex algorithms and data handling techniques.
Advantages Of Linear Data Structures
Linear data structures offer several benefits, making them a preferred choice in various applications. Here are some key advantages:
1. Simplicity
The linear arrangement in linear data structures is straightforward, easy to implement, understand and use. It is also easier to manipulate or modify them (in comparison to non-linear structures).
2. Efficient Memory Utilization
Linear data structures efficiently utilize memory space, as elements are stored sequentially. For example, in arrays, memory allocation is contiguous, which minimizes the overhead of memory management. Also in linked lists allow dynamic memory allocation and can grow or shrink as needed, thus optimizing memory usage.
3. Ease of Traversal
Linear data structures facilitate easy and straightforward traversal of elements, making operations like searching, sorting, and updating more manageable. Since elements are arranged in a sequence, moving from one element to the next is simple and direct. This ordered nature supports the efficient execution of various algorithms that require element access and manipulation.
4. Sequential Access
Linear data structures provide efficient sequential access to elements, ideal for algorithms requiring ordered data processing. Operations that require accessing elements in a specific order benefit from the sequential nature of linear data structures. This is particularly useful in applications like streaming data processing, where data is processed in the order it is received.
5. Predictable Performance
The time complexity of basic operations (insertion, deletion, access) in linear data structures is predictable and often constant or linear, making performance analysis straightforward. This further simplifies the analysis and optimization of algorithms. For example, accessing an element in an array has a constant time complexity (O(1)), while traversing a linked list has a linear time complexity (O(n)).
6. Versatility
Linear data structures can implement more complex data structures and algorithms, serving as building blocks for stacks, queues, and hash tables. Arrays and linked lists can be adapted and extended to create more sophisticated data structures. For example, a stack can be implemented using an array or a linked list, and queues can be efficiently managed using linked lists.
7. Efficient Sorting and Searching
Linear data structures can be easily sorted and searched using well-known algorithms, enhancing their utility in various applications. Algorithms like quicksort and binary search work efficiently with linear data structures, leveraging their ordered nature to optimize performance. This makes linear data structures suitable for frequent data retrieval and organization applications.
8. Compatibility with Hardware
Linear data structures align well with the underlying hardware architecture, such as CPU caching and memory access patterns, resulting in optimized performance. For example, the contiguous memory allocation in arrays aligns with how modern CPUs cache data, leading to faster access times and improved performance. Linked lists, while non-contiguous, still benefit from sequential access patterns that match typical memory usage scenarios.
9. Ease of Implementation
Many programming languages offer built-in support for linear data structures, simplifying their implementation and use. Languages like C, C++, Java, and Python provide built-in array and linked list structures, along with libraries and functions to manipulate them. This built-in support makes it easier for developers to use these data structures without implementing them from scratch.
10. Order Preservation
Linear data structures preserve the order of elements, which is essential in many applications where the sequence of data matters such as task scheduling.
11. Flexibility
Linear data structures can be adapted to various use cases, providing flexibility in application design. For instance, arrays can be used for static data storage with fixed size, while linked lists offer dynamic size adjustments. This flexibility allows developers to choose the most appropriate linear data structure based on the specific needs of their application.
These advantages highlight why linear data structures are widely used and remain fundamental in both educational contexts and real-world applications.
What Is Nonlinear Data Structure?
Non-linear data structures are types of data structures where data elements are not arranged sequentially or linearly. Unlike linear data structures, non-linear data structures organize data in a hierarchical manner, allowing for multiple relationships among the elements.
- Non-linear data structures enable more complex data relationships and structures, which are essential for representing hierarchical and networked data.
- These structures include trees and graphs, commonly used in various applications like database management, networking, and artificial intelligence.
- Non-linear data structures are advantageous when dealing with data that requires flexible and intricate connections.
- They help in optimizing various operations such as searching, inserting, and deleting data, making them crucial for complex problem-solving scenarios.
Difference Between Linear & Non-Linear Data Structures
Understanding the differences between linear and non-linear data structures is crucial for selecting the appropriate structure for your application. The table below highlights the key differences between them:
| Basis/Parameter | Linear Data Structures | Non-Linear Data Structures |
|---|---|---|
| Arrangement | Elements are arranged in a sequential order | Elements are arranged hierarchically or in a network |
| Memory Utilization | Generally uses contiguous memory locations | Can use both contiguous and non-contiguous memory |
| Traversal | Linear traversal (one element after another) | Hierarchical traversal (parent-child relationships) |
| Complexity | Simpler to implement and understand | More complex in terms of implementation and understanding |
| Examples | Arrays, Linked Lists, Stacks, Queues | Trees, Graphs |
| Access Time | Typically, faster access times due to the sequential nature | Access time can vary depending on structure and hierarchy |
| Use Cases | Suitable for simple, linear data processing | Ideal for complex data relationships and hierarchical data |
| Flexibility | Less flexible, as structure size may be fixed (like arrays) | More flexible, can grow or shrink dynamically (like trees) |
For more information, read- What is The Difference Between Linear And Non Linear Data Structure?
Who Uses Linear Data Structures?
Linear data structures are utilized across various fields and applications due to their simplicity, efficiency, and versatility. Here are some key users and applications of linear data structures:
- Software Development: Linear data structures are fundamental in software development for organizing and managing data efficiently. They are used in applications ranging from simple data storage to complex algorithms and data processing tasks.
- Database Management Systems: Linear data structures play a key role in managing and organizing large data sets. For example, arrays and linked lists are employed in database systems to store and retrieve records sequentially.
- Operating Systems: Linear data structures are essential components of operating systems for managing memory allocation, process scheduling, and file systems. For example, arrays and linked lists are often used to store and manage system data structures.
- Web Development: Linear data structures are used in web development frameworks and applications for managing user sessions, storing user data, and handling server-side operations efficiently.
- Networking: Linear data structures like queues are employed in networking protocols for managing packet transmission and ensuring data flow control.
- Artificial Intelligence and Machine Learning: Linear data structures play a significant role in AI and ML algorithms for storing and processing large datasets. They are used in data preprocessing, feature extraction, and model training phases.
- Education and Academics: Linear data structures are extensively taught and used in educational settings to teach fundamental programming concepts, algorithms, and data handling techniques.
- Financial Applications: Linear data structures are used in financial applications for managing transactions, storing account information, and performing calculations efficiently.
- Embedded Systems: Linear data structures are employed in embedded systems programming for efficient memory management, data handling, and real-time processing tasks.
- Gaming and Graphics: Linear data structures are used in game development and graphics programming to manage game states, render objects, and handle user inputs.
As is evident, linear data structures are widely used across various domains and industries, given their versatility and crucial role in modern computing.
Conclusion
Linear data structures are indispensable tools in modern computing, providing efficient ways to organize and manipulate data. Every linear data structure type, including arrays, linked lists, stacks, and queues, offers distinct advantages tailored to specific tasks. These data structures have a wide range of applications across domains like software development, database management, optimizing network operations, artificial intelligence, financial systems, etc.
Linear data structures not only streamline data management but also enable seamless implementation of algorithms and processes. By mastering linear data structures, professionals across diverse industries can enhance system efficiency, improve data handling capabilities, and innovate with confidence.
Frequently Asked Questions
Q. What is an element in a data structure?
An element in a data structure refers to a single unit of data that is stored within the structure. It could be a number, character, object, or any other data type, depending on the structure. Elements are organized and manipulated according to the rules and operations defined by the respective linear data structure.
Q. Is heap a linear data structure?
No, a heap is not a linear data structure. It is a hierarchical data structure that follows the heap property, which specifies the relationship between parent and child nodes. Heaps are typically implemented using arrays, but they do not have a linear arrangement like arrays or linked lists.
Q. What is linear search in an array?
Linear search in an array is a simple searching algorithm where each element of the array is sequentially checked until the target element is found or the end of the array is reached. It has a time complexity of O(n), where n is the number of elements in the array.
Q. What is binary search?
Binary search is an efficient searching algorithm used on sorted arrays or lists. It works by repeatedly dividing the search interval in half until the target element is found or the interval is empty. It has a time complexity of O(log n), making it significantly faster than linear search for large datasets.
Q. What are some disadvantages of linear data structures?
Some disadvantages of linear data structures include:
- Limited Flexibility: Linear structures like arrays have fixed sizes, making it difficult to adjust dynamically.
- Inefficient Insertions and Deletions: Insertions and deletions can be inefficient in arrays, especially when elements need to be shifted.
- Limited Search Capabilities: Linear search algorithms can be slower compared to more advanced search algorithms like binary search.
- Lack of Hierarchical Organization: Linear data structures do not support hierarchical relationships between elements, limiting their use for certain types of data.
This compiles our discussion on what is linear data structure. Here are a few more interesting topics you must explore:
- 40+ Frequently Asked DBMS Interview Questions With Answers (2024)
- Most Common Programming Interview Questions With Answers 2024
- Data Structure Interview Questions For 2024 [With Detailed Answers]
- 53 Frequently Asked Linked List Interview Questions With Answers 2024
- Difference Between Structured and Unstructured Data Explained
An economics graduate with a passion for storytelling, I thrive on crafting content that blends creativity with technical insight. At Unstop, I create in-depth, SEO-driven content that simplifies complex tech topics and covers a wide array of subjects, all designed to inform, engage, and inspire our readers. My goal is to empower others to truly #BeUnstoppable through content that resonates. When I’m not writing, you’ll find me immersed in art, food, or lost in a good book—constantly drawing inspiration from the world around me.
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter












Comments
Add comment