- What Is Data Structure?
- Key Features Of Data Structures
- Basic Terminologies Related To Data Structures
- Types Of Data Structures
- What Are Linear Data Structures & Its Types?
- What Are Non-Linear Data Structures & Its Types?
- Importance Of Data Structure In Programming
- Basic Operations On Data Structures
- Applications Of Data Structures
- Real-Life Applications Of Data Structures
- Linear Vs. Non-linear Data Structures
- What Are Algorithms? The Difference Between Data Structures & Algorithms
- Conclusion
- Frequently Asked Questions
- What Is Asymptotic Notation?
- How Asymptotic Notation Helps In Analyzing Performance
- Types Of Asymptotic Notation
- Big-O Notation (O)
- Omega Notation (Ω)
- Theta Notation (Θ)
- Little-O Notation (o)
- Little-Omega Notation (ω)
- Summary Of Asymptotic Notations
- Real-World Applications Of Asymptotic Notation
- Conclusion
- Frequently Asked Questions
- Understanding Big O Notation
- Types Of Time Complexity
- Space Complexity In Big O Notation
- How To Determine Big O Complexity
- Best, Worst, And Average Case Complexity
- Applications Of Big O Notation
- Conclusion
- Frequently Asked Questions
- What Is Time Complexity?
- Why Do You Need To Calculate Time Complexity?
- The Time Complexity Algorithm Cases
- Time Complexity: Different Types Of Asymptotic Notations
- How To Calculate Time Complexity?
- Time Complexity Of Sorting Algorithms
- Time Complexity Of Searching Algorithms
- Writing And optimizing An algorithm
- What Is Space Complexity And Its Significance?
- Relation Between Time And Space Complexity
- Conclusion
- What Is Linear Data Structure?
- Key Characteristics Of Linear Data Structures
- What Are The Types Of Linear Data Structures?
- What Is An Array Linear Data Structure?
- What Are Linked Lists Linear Data Structure?
- What Is A Stack Linear Data Structure?
- What Is A Queue Linear Data Structure?
- Most Common Operations Performed in Linear Data Structures
- Advantages Of Linear Data Structures
- What Is Nonlinear Data Structure?
- Difference Between Linear & Non-Linear Data Structures
- Who Uses Linear Data Structures?
- Conclusion
- Frequently Asked Questions
- What is a linear data structure?
- What is a non-linear data structure?
- Difference between linear data structure and non-linear data structure
- FAQs about linear and non-linear data structures
- What Is Search?
- What Is Linear Search In Data Structure?
- What Is Linear Search Algorithm?
- Working Of Linear Search Algorithm
- Complexity Of Linear Search Algorithm In Data Structures
- Implementations Of Linear Search Algorithm In Different Programming Languages
- Real-World Applications Of Linear Search In Data Structure
- Advantages & Disadvantages Of Linear Search
- Best Practices For Using Linear Search Algorithm
- Conclusion
- Frequently Asked Questions
- What Is The Binary Search Algorithm?
- Conditions For Using Binary Search
- Steps For Implementing Binary Search
- Iterative Method For Binary Search With Implementation Examples
- Recursive Method For Binary Search
- Complexity Analysis Of Binary Search Algorithm
- Iterative Vs. Recursive Implementation Of Binary Search
- Advantages & Disadvantages Of Binary Search
- Practical Applications & Real-World Examples Of Binary Search
- Conclusion
- Frequently Asked Questions
- Understanding The Jump Search Algorithm
- How Jump Search Works?
- Code Implementation Of Jump Search Algorithm
- Time And Space Complexity Analysis
- Advantages Of Jump Search
- Disadvantages Of Jump Search
- Applications Of Jump Search
- Conclusion
- Frequently Asked Questions
- What Is Sorting In Data Structures?
- What Is Bubble Sort?
- What Is Selection Sort?
- What Is Insertion Sort?
- What Is Merge Sort?
- What Is Quick Sort?
- What Is Heap Sort?
- What Is Radix Sort?
- What Is Bucket Sort?
- What Is Counting Sort?
- What Is Shell Sort?
- Choosing The Right Sorting Algorithm
- Applications Of Sorting
- Conclusion
- Frequently Asked Questions
- Understanding Bubble Sort Algorithm
- Bubble Sort Algorithm
- Implementation Of Bubble Sort In C++
- Time And Space Complexity Analysis Of Bubble Sort Algorithm
- Advantages Of Bubble Sort Algorithm
- Disadvantages Of Bubble Sort Algorithm
- Applications of Bubble Sort Algorithms
- Conclusion
- Frequently Asked Questions
- Understanding The Merge Sort Algorithm
- Algorithm For Merge Sort
- Implementation Of Merge Sort In C++
- Time And Space Complexity Analysis Of Merge Sort
- Advantages And Disadvantages Of Merge Sort
- Applications Of Merge Sort
- Conclusion
- Frequently Asked Questions
- Understanding The Selection Sort Algorithm
- Algorithmic Approach To Selection Sort
- Implementation Of Selection Sort Algorithm
- Complexity Analysis Of Selection Sort
- Comparison Of Selection Sort With Other Sorting Algorithms
- Advantages And Disadvantages Of Selection Sort
- Application Of Selection Sort
- Conclusion
- Frequently Asked Questions
- What Is Insertion Sort Algorithm?
- How Does Insertion Sort Work? (Step-by-Step Explanation)
- Implementation of Insertion Sort in C++
- Time And Space Complexity Of Insertion Sort
- Applications Of Insertion Sort Algorithm
- Comparison With Other Sorting Algorithms
- Conclusion
- Frequently Asked Questions
- Understanding Quick Sort Algorithm
- Step-By-Step Working Of Quick Sort
- Implementation Of Quick Sort Algorithm
- Time Complexity Analysis Of Quick Sort
- Advantages Of Quick Sort Algorithm
- Disadvantages Of Quick Sort Algorithm
- Applications Of Quick Sort Algorithm
- Conclusion
- Frequently Asked Questions
- Understanding The Heap Data Structure
- Working Of Heap Sort Algorithm
- Implementation Of Heap Sort Algorithm
- Advantages Of Heap Sort
- Disadvantages Of Heap Sort
- Real-World Applications Of Heap Sort
- Conclusion
- Frequently Asked Questions
- Understanding The Counting Sort Algorithm
- Conditions For Using Counting Sort Algorithm
- How Counting Sort Algorithm Works?
- Implementation Of Counting Sort Algorithm
- Time And Space Complexity Analysis Of Counting Sort
- Comparison Of Counting Sort With Other Sorting Algorithms
- Advantages Of Counting Sort Algorithm
- Disadvantages Of Counting Sort Algorithm
- Applications Of Counting Sort Algorithm
- Conclusion
- Frequently Asked Questions
- Understanding Shell Sort Algorithm
- Working Of Shell Sort Algorithm
- Implementation Of Shell Sort Algorithm
- Time Complexity Analysis Of Shell Sort Algorithm
- Advantages Of Shell Sort Algorithm
- Disadvantages Of Shell Sort Algorithm
- Applications Of Shell Sort Algorithm
- Conclusion
- Frequently Asked Questions
- What Is Linked List In Data Structures?
- Types Of Linked Lists In Data Structures
- Linked List Operations In Data Structures
- Advantages And Disadvantages Of Linked Lists In Data Structures
- Comparison Of Linked Lists And Arrays
- Applications Of Linked Lists
- Conclusion
- Frequently Asked Questions
- What Is A Singly Linked List In Data Structure?
- Insertion Operations On Singly Linked Lists
- Deletion Operation On Singly Linked List
- Searching For Elements In Single Linked List
- Calculating Length Of Single Linked List
- Practical Applications Of Singly Linked Lists In Data Structure
- Common Problems With Singly Linked Lists
- Conclusion
- Frequently Asked Questions (FAQ)
- What Is A Linked List?
- Reverse A Linked List
- How To Reverse A Linked List? (Approaches)
- Recursive Approach To Reverse A Linked List
- Iterative Approach To Reverse A Linked List
- Using Stack To Reverse A Linked List
- Complexity Analysis Of Different Approaches To Reverse A Linked List
- Conclusion
- Frequently Asked Questions
- What Is A Stack In Data Structure?
- Understanding Stack Operations
- Stack Implementation In Data Structures
- Stack Implementation Using Arrays
- Stack Implementation Using Linked Lists
- Comparison: Array vs. Linked List Implementation
- Applications Of Stack In Data Structures
- Advantages And Disadvantages Of Stack Data Structure
- Conclusion
- Frequently Asked Questions
- What Is A Graph Data Structure?
- Importance Of Graph Data Structures
- Types Of Graphs In Data Structure
- Types Of Graph Algorithms
- Application Of Graphs In Data Structures
- Challenges And Complexities In Graphs
- Conclusion
- Frequently Asked Questions
- What Is Tree Data Structure?
- Terminologies Of Tree Data Structure:
- Different Types Of Tree Data Structures
- Basic Operations On Tree Data Structure
- Applications Of Tree Data Structures
- Comparison Of Trees, Graphs, And Linear Data Structures
- Advantages Of Tree Data Structure
- Disadvantages Of Tree Data Structure
- Conclusion
- Frequently Asked Questions
- What Is Dynamic Programming?
- Real-Life Example: The Jigsaw Puzzle Analogy
- How To Solve A Problem Using Dynamic Programming?
- Dynamic Programming Algorithm Techniques
- Advantages Of Dynamic Programming
- Disadvantages Of Dynamic Programming
- Applications Of Dynamic Programming
- Conclusion
- Frequently Asked Questions
- Understanding The Sliding Window Algorithm
- How Does The Sliding Window Algorithm Works?
- How To Identify Sliding Window Problems?
- Fixed-Size Sliding Window Example: Maximum Sum Subarray Of Size k
- Variable-Size Sliding Window Example: Smallest Subarray With A Given Sum
- Advantages Of Sliding Window Technique
- Disadvantages Of Sliding Window Technique
- Conclusion
- Frequently Asked Questions
- Introduction To Data Structures
- Data Structures Interview Questions: Basics
- Data Structures Interview Questions: Intermediate
- Data Structures Interview Questions: Advanced
- Conclusion
Time Complexity Of Algorithms: Types, Notations, Cases, and More
If you are studying computer science, you should have seen the notations of temporal complexity in some way or another. You should familiarize yourself with the concept of the running time complexity of algorithms as soon as possible because there is not a single technical interview that requires you to determine the running time complexity of a program. For most competitive programming languages you need to learn about time complexity.
What Is Time Complexity?
About the size of the input data, the number of operations that an algorithm must carry out to fulfill its task is referred to as the time complexity (considering each operation takes a constant time). It is generally agreed that the most effective algorithm is the one that can carry out the desired result with the fewest number of steps.
We overlook those external constant factors and are solely concerned about the number of times a particular statement is now being executed about the size of the input data. The amount of time it takes for an algorithm to complete its task is contingent not only on the computing speed of such a system that you are now using but also on the amount of time it takes the algorithm to process the data it receives. Let's say the amount of actual time needed to execute a single statement is one second; in such a case, how much unit time is needed to execute statements? This should take seconds for it to finish.

Why Do You Need To Calculate Time Complexity?
Using different problem-solving techniques might result in a variety of different outcomes when attempting to tackle the same issue. An assessment of the resources that are necessary for an algorithm to solve particular computer issues can be obtained through the use of algorithm analysis. In addition, the amount of time, memory space, plus resources that are required to carry out the execution can be figured out.
The time complexity of an algorithm is a metric that may be used to quantify the amount of time required for an algorithm to run as just a function of the length of the input. The space complexity of the algorithm is the measurement of how much memory or storage space it requires to run, and it is expressed as binary search functions of the amount of such data that is being processed.
1. Binary search algorithm
Finding an object in a sorted list of objects can be done quickly and effectively with the use of an algorithm called binary search. It works by continually dividing the area of the list in half that might contain the object until you have reduced the possible places to just one. This process continues until the list has only one viable location.
2. Linked list with data structures
It is a type of data structure known as a linear data structure or a succession of data objects in which the data pieces are not stored at memory locations that are contiguous to one another. The elements are connected by pointers, which results in the formation of a chain. Each component has its distinct object, which is referred to as a node. Each node contains two pieces of information: a data field as well as a reference toward the following node in the hierarchy. The beginning of a chain of connected items is referred to as the head of the linked list. When the list is empty, the head of the list is a null reference, and the node that is at the very end of the list also has a reference to the null value.
A linked list is an example of a dynamic data structure where the total number of nodes within the list is not predetermined; rather, the list can expand or contract according to the needs of the application.
3. BFS algorithm
The “Breadth-First Search” (BFS) algorithm is used to traverse graphs. It begins its journey across the graph at the node that serves as its origin and continues to investigate all of the nodes that border it. It chooses the node on the boundary and then navigates to all of the nodes that have not been explored previously. The algorithm repeats the same procedure for every neighboring node up until the point where it reaches the ambitious state.
4. Asymptotic notation and depth-first search algorithm
The asymptotic notation is utilized when describing the maximum algorithm with runtimes, also known as the amount of minimum time it takes for an algorithm to complete its task when given a certain number of inputs. There are 3 separate complex notations, which are denoted as follows: big Oh notation, big Theta notation, and big Omega notation.
Depth-first search technique is utilized in topological sorting, scheduling issues, cycle identification in graphs, and the resolution of puzzles with just one solution, including mazes and sudoku puzzles. Other uses include the careful analysis of networks, such as determining whether or not a graph has a bipartite structure.
The Time Complexity Algorithm Cases
- Best case: This is the time limit at which an algorithm can be run. We must be familiar with the scenario that results in the fewest amount of procedures being carried out. In the illustration, our array is [1, 2, 3, 4, 5], and the question we are attempting to answer is whether or not the number "1" is contained within the array. Now that you've made only one comparison, you should be able to deduce that the element in question is indeed contained within the array. Therefore, this represents the best possible outcome of your program.
- Average case: We first determine the amount of time required to complete the task based on each of the many inputs that could be used, then we add up all of the results, and finally, we divide the total by the total number of inputs. We must be aware of (or can forecast) the distribution of cases.
- Worst case: This is the upper bound on the amount of time it takes for an algorithm to complete its task. We must identify the scenario that results in the highest possible number of arithmetic operations being carried out. In the context of this discussion, the worst possible scenario would be if the array that was provided to us was [1, 2, 3, 4, 5], and we tried to determine whether or not the element "6" was included in the array. Following the completion of the if-condition of our loop's iteration five times, the algorithm will provide the value "0" as the final result.
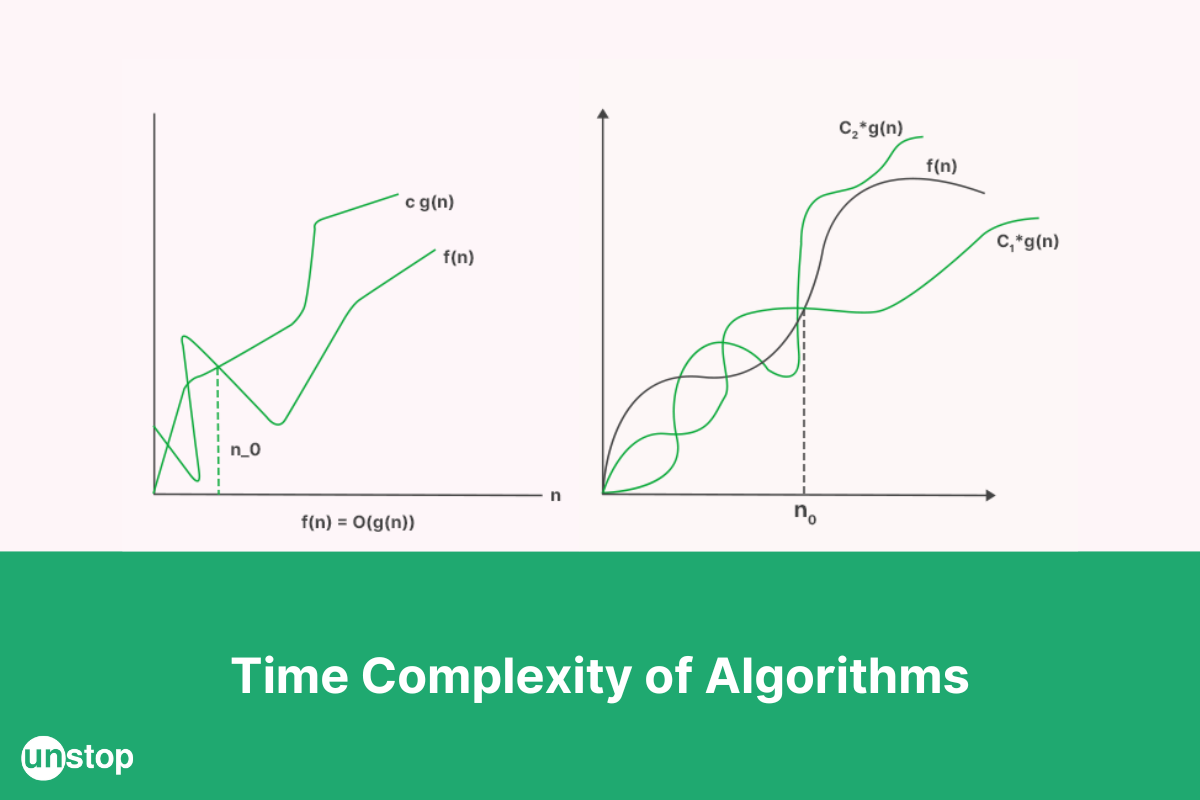
Time Complexity: Different Types Of Asymptotic Notations
Asymptotic notations are the mathematical tools to determine the time complexity of an algorithm. The following are the three different types of time complexity asymptotic notations:
1. Big-Theta (Θ) notation (+Small theta)
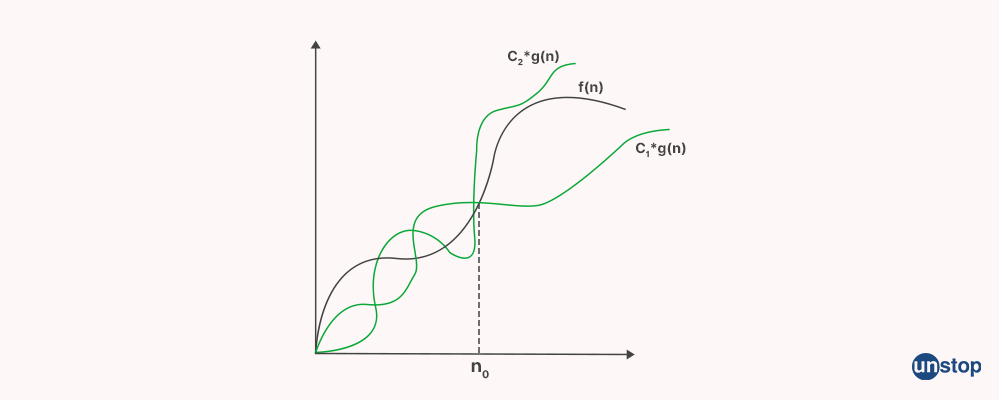
Theta encloses functions from both the lower and upper sides. Theta notation is used to describe the average time of the algorithm as it describes the lowers and the upper bound of the function.
Θ (g(n)) = {f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1 * g(n) ≤ f(n) ≤ c2 * g(n) for all n ≥ n0}
Note: Θ(g) is a set
2. Big-Oh (O) notation
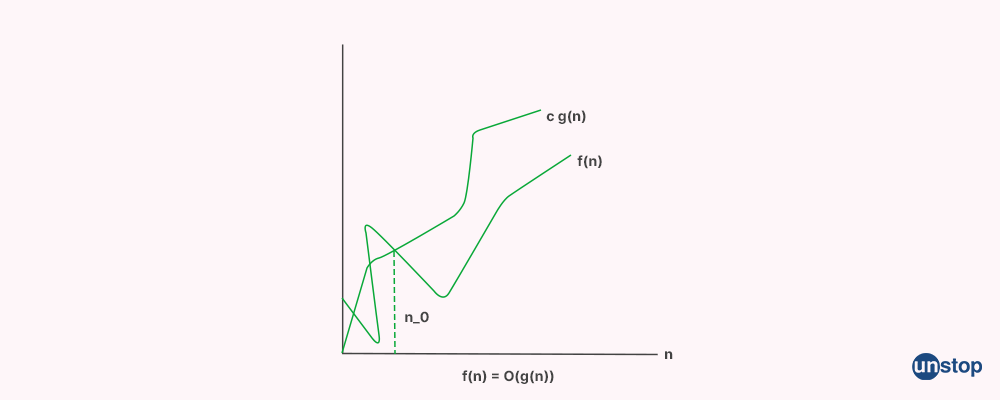
Big-O notation describes the upper bound or worst-case time complexity of an algorithm. It provides an asymptotic analysis of an algorithm's performance, focusing on how the runtime grows as the input size increases. For instance, in a linear search algorithm, the best-case time complexity is O(1) when the target element is found at the beginning of the list, and the worst-case time complexity is O(n) when the target element is at the end or not present at all. Therefore, the Big-O notation for linear search is O(n), as it represents the maximum time taken by the algorithm.
O(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }
3. Big-Omega (Ω) notation (+Small omega)
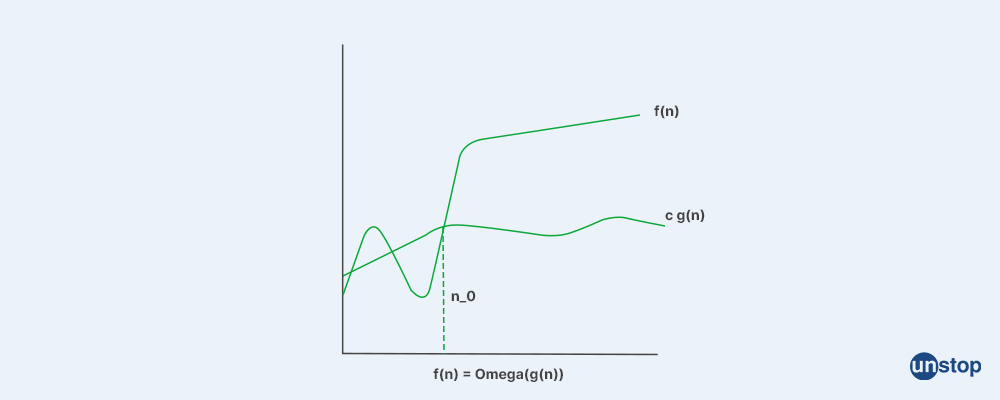
Omega notation gives the lower bound or the best-case running time of an algorithm's time complexity. In simple words, it gives the minimum time required by the algorithm.
Ωg(n) = { f(n): there exist positive constants c and n0 such that 0 ≤ c*g(n) ≤ f(n) for all n ≥ n0}
Note: Ω (g) is a set
Consider the example of selection sort where it takes O(1) in the best case and O(n^2) in the worst case. Now the Omega will be the O(1) as it is the lower bound of the algorithm.
The following steps are followed for calculating the Big - Omega (Ω) for any program:
- First, take the program and break them into smaller segments.
- Find the number of operations performed for each segment (in terms of the input size) assuming the given input is such that the program takes the least amount of time.
- Add up all the operations and calculate the time. Say it comes out to be f(n).
- Remove all the constants and choose the term having the least order or any other function which is always less than f(n) when n tends to infinity. Let's say it is g(n) then, Big - Omega (Ω) of f(n) is Ω(g(n)).
How To Calculate Time Complexity?
Good knowledge of calculating different types of time complexity lets us make informed decisions regarding algorithm design, optimization, and performance analysis.
In simple terms, the process of calculating the time complexity of an algorithm involves analyzing the number of operations performed as a function of the input size, enabling us to estimate its efficiency and scalability.
Constant Time Complexity Analysis: O(1)
Calculating the time complexity of an algorithm with constant time complexity is simple and straightforward. It indicates that the algorithm's runtime remains constant, regardless of the input size. It forbids the use of loops, recursion call, and calls to any other function having non-linear time.
For Example: When we search for an element in an array (say arr[]) with arr[1] so it's a constant time complexity.
swap function is also a constant time algorithm i.e. O(1)
Here C is a constant term (pre-defined in the code and not taken as input from the user)
for(int i=0;i<C;i++){
//having O(1) time complexity
}
Linear Time Complexity: O(n)
Linear time complexity denoted as O(n), involves analyzing the number of operations performed in proportion to the input size (n). Calculating the time complexity of an algorithm with linear time complexity involves identifying the key operations, counting iterations, and observing how the algorithm's runtime grows in a linear fashion as the input size increases.
//Here c is a constant
for(int i=0;i<n;i+=c){
//Here n is a variable
}
// In recursive Algorithm
void recursion(int n ){
if(n==1) return;
else{
// constant time expression only
}
recursion(n-1)
}
Explanation:
In the first snippet, we have a for loop that runs in linear time complexity. The loop iterates from 0 to n, incrementing the loop variable by a constant amount (c) in each iteration. Since the loop variable changes by a constant value, the time complexity is O(n). This means the runtime of the loop increases linearly with the input size (n).
While the time complexity of the recursive algorithm in the second snippet can vary depending on the presence and dominance of constant time expressions.
Quadratic Time Complexity: O(n²)
The time complexity of a function or loop statement is considered as O(n^2), and when there is a linear loop inside a linear loop, it is considered as quadratic time complexity.
for(int i=0;i<n;i++){
//here n is variable
//linear loop taking 0(n) time
for(int j=0;j<n;j++){
//loop inside a loop it also takes 0(n)
}
}
Explanation:
In the code, we have an outer for loop that iterates from 0 to n, with n being a variable. Inside the outer loop, there is an inner for loop that also iterates from 0 to n. This creates a nested loop structure where the inner loop is executed multiple times for each iteration of the outer loop.
The time complexity of the outer loop itself is O(n) because it runs linearly with the input size (n). Similarly, the inner loop also has a time complexity of O(n) as it iterates n times.
When we have a nested loop structure like this, the time complexity is determined by multiplying the time complexities of the individual loops. In this case,
O(n)*O(n) = o(n^2)
This multiplication is only done because it is a case of nested loop (loop inside a loop).
Similarly, if there are ‘m’ loops defined in the function, then the order is given by O (n ^ m), which are called polynomial time complexity functions.
Logarithmic Time Complexity: O(log n)
In algorithms with logarithmic time complexity, the loop variables are typically multiplied or divided by a constant amount. This pattern is commonly seen in algorithms like Binary Tree and Binary Search.
//here c is a constant
for(int i =1;i<n;i*=c){
//some O(1) expression
}
for(int i=1;i<n;i/=c){
// some O(1) expression
}
Explanation:
In the First loop, we are multiplying the variable ''with c in every iteration so it becomes 1,c,c^2,c^3,...…,c^k.
If we put k equals to Logcn, we get cLogcn which is n.
So here our Input data size shrinks after every iteration as -
1st Iteration i=1 && i becomes i*2 = 2
2nd Iteration i=2 && becomes I*2 = 4;
3rd Iteration i=4 && becomes i*2 = 8
and...so on
This means that after every iteration, our input data size shrinks so the algorithm is knowns as logarithms.
Exponential Time Complexity: O(2^n)
An exponential time algorithm refers to an algorithm that increases rapidly in magnitude as the input data grows. This type of algorithm is commonly found in recursive algorithms, where at each step, there are two possible options or paths to explore.
Through each iteration, the algorithm progressively divides the problem space until it reaches a stopping point defined by a base condition. The exponential growth arises from the branching nature of the algorithm, as the number of possibilities doubles with each iteration.
The Fibonacci series would be a great example of explaining the exponential time complexity. Below is the code of the Fibonacci series:
long int fib(int n){
//base condition
if(n<=1) return n;
//for every, we are calling to fib two times with different input
return fib(n-1)+fib(n-2);
}
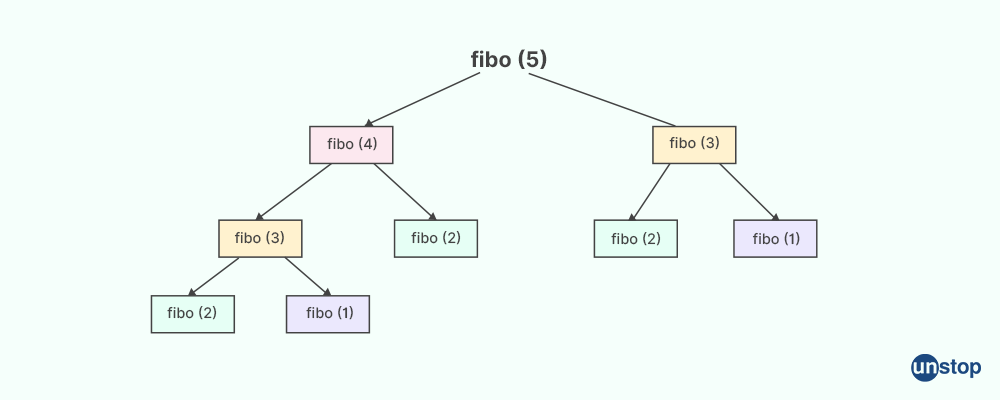
For example, if we give the input fib(5) the code goes like this -
Explanation:
In the fib function, we work with a recursive approach to calculate the Fibonacci sequence. To begin, we define a base condition that acts as the stopping point for the recursion. For any given input, we make recursive calls to fib(n-1) and fib(n-2) to calculate the values of the previous two elements in the Fibonacci sequence. The problem is repeatedly divided into smaller subproblems, and when we reach the base condition, the recursion ends and the final Fibonacci number is calculated.
Polynomial Time Complexity: O(n^c)
Polynomial time complexity, denoted as O(n^c), arises in situations with nested loops where 'c' represents the number of loops nested within each other. Each loop has a time complexity of O(n), meaning it scales linearly with the input size (n).
When we have 'c' nested loops, the time complexity is determined by multiplying the time complexities of each loop together. This can be expressed as -
O(n) * O(n) * O(n) * ..... upto c time = O(n^c)
It's important to note that polynomial time complexity can also occur in various other scenarios besides nested loops, depending on the problem and algorithm being analyzed.
Linearithmic: O(n log n)
Linearithmic time complexity is observed when there is a nested loop structure where the outer loop runs in linear time and the inner loop exhibits a time complexity of O(log n).
//here C is a constant
for(int i=0i<n;i+=C){
//this loop take O(n)
for(int j=0;j<n;j*=C){
//this loop takes O(logn) as discussed above
}
}
Explanation:
So here we have two loops - the outer loop takes O(n) and the Inner loop takes O(logn) so the time complexity becomes:-
O(n )* O(logn) = O(nlogn)
In this scenario, the outer loop iterates through the input in a linear manner, meaning its execution time grows linearly with the input size (n). Inside this outer loop, there is an inner loop that operates with a time complexity of O(log n). This implies that the inner loop's execution time increases logarithmically with the input size. This means the overall time complexity of the code, considering both the linear outer loop and the logarithmic inner loop, is expressed as O(n log n).
Time Complexity Of Sorting Algorithms
Understanding the time complexity of different sorting techniques will lead to a good understanding of the time complexity.
1. Selection Sort
It has O(n^2) time complexity in the best case, the average case as well as in the worst case.
2. Merge Sort
It has O(NlogN) time complexity in the best case, the average case as well as in the worst case.
3. Bubble Sort
This is the simplest sorting algorithm. it has an O(n^2) time complexity in both the worst as well as best-case.
4. Quick Sort
It has O(NlogN) complexity in the best and average case. But in the worst case, it becomes O(N^2).
5. Heap Sort
It has O(NlogN) time complexity in the best case, the average case as well as in the worst case.
6. Bucket Sort
It has O(N+k) complexity in the best and average case. But in the worst case, it becomes O(N^2).
7. Insertion Sort
The time complexity of the insertion sort algorithm in the best case is O(n) and in the worst case, it is O(n^2).
Time Complexity Of Searching Algorithms
Let's delve into the time complexity of various search algorithms.
Time Complexity of Linear Search Algorithm
Linear search is also called a sequential search algorithm. It is the simplest search algorithm. In Linear search, we simply traverse the list completely and match each element of the list with the item whose location is to be found. If the match is found, then the location of the item is returned; otherwise, the algorithm returns NULL. Its time complexity in different scenarios is as follows:
| Case | Time Complexity |
| Best Case | O(1) |
| Average Case | O(n) |
| Worst Case | O(n) |
Time Complexity of Binary Search Algorithm
Binary Search is an efficient searching algorithm specifically designed for sorted arrays. It works by dividing the search interval in half at each step, utilizing the fact that the array is already sorted. This approach drastically reduces the time complexity to O(log N), making it highly efficient for large arrays. It's time complexities in different scenarios are as follows:
| Case | Time Complexity |
| Best Case | O(1) |
| Average case | O(logN) |
| Worst Case | O(logN) |
Writing And Optimizing An Algorithm
Optimizing an algorithm means writing cleaner and more understandable code that can be easily comprehended by others.
We are going to see the optimized code for the sorting algorithm. Specifically, we will be focusing on the Bubble sort algorithm which has a time complexity of O(n^2) time in best and worst cases.
Example 1:
CODE SNIPPET IS HEREdm9pZCBidWJibGVTb3J0KGludCBhcnJbXSwgaW50IG4pCnsKaW50IGksIGo7CmZvciAoaSA9IDA7IGkgPCBuIC0gMTsgaSsrKQoKLy8gTGFzdCBpIGVsZW1lbnRzIGFyZSBhbHJlYWR5Ci8vIGluIHBsYWNlCmZvciAoaiA9IDA7IGogPCBuIC0gaSAtIDE7IGorKykKaWYgKGFycltqXSA+IGFycltqICsgMV0pCnN3YXAoYXJyW2pdLCBhcnJbaiArIDFdKTsKfQ==
Explanation:
The reason why this code always has a time complexity of O(n^2) is that for every outer loop, you have to travel the inner loop. There is no way that you can skip the inner loop condition.
However, there are some sorting algorithms that are more efficient than this. For example, Merge Sort is considered one of the fastest and more optimized sorting algorithms.
Example 2:
CODE SNIPPET IS HEREdm9pZCBtZXJnZShpbnQgYXJyW10sIGludCBsb3csIGludCBtaWQsIGludCBoaWdoKQp7Ci8vIFlvdXIgY29kZSBoZXJlCnZlY3RvcjxpbnQ+IHRlbXA7CmludCBsZWZ0PWxvdzsKaW50IHJpZ2h0PW1pZCsxOwp3aGlsZShsZWZ0PD1taWQgJiYgcmlnaHQ8PWhpZ2gpCnsKaWYoYXJyW2xlZnRdPD1hcnJbcmlnaHRdKQp7CnRlbXAucHVzaF9iYWNrKGFycltsZWZ0XSk7CmxlZnQrKzsKfQplbHNlCnsKdGVtcC5wdXNoX2JhY2soYXJyW3JpZ2h0XSk7CnJpZ2h0Kys7Cn0KfQp3aGlsZShsZWZ0PD1taWQpCnsKdGVtcC5wdXNoX2JhY2soYXJyW2xlZnRdKTsKbGVmdCsrOwp9CndoaWxlKHJpZ2h0PD1oaWdoKQp7CnRlbXAucHVzaF9iYWNrKGFycltyaWdodF0pOwpyaWdodCsrOwp9CmZvcihpbnQgaT1sb3c7aTw9aGlnaDtpKyspCnsKYXJyW2ldPXRlbXBbaS1sb3ddOwp9Cn0KCnZvaWQgbWVyZ2VTb3J0KGludCBhcnJbXSwgaW50IGwsIGludCByKQp7Ci8vY29kZSBoZXJlCmlmKGw+PXIpIHJldHVybjsKaW50IG1pZCA9IChsK3IpLzI7Cm1lcmdlU29ydChhcnIsbCxtaWQpOwptZXJnZVNvcnQoYXJyLG1pZCsxLHIpOwptZXJnZShhcnIsbCxtaWQscik7Cn0=
Explanation:
Merge Sort is a sorting algorithm that divides the array into smaller subarrays, sorting them and merging them in the final step so you get a sorted array in the final result. This code starts with the function mergeSort which is called from the main function. You are given low and high, then you find the mid and divide the given array into two subarrays. This continues until you are left with a single element.
Then function merge is called to merge the elements in sorted order (i.e. ascending order), ensuring efficient sorting with a time complexity of O(nlogn).
What Is Space Complexity And Its Significance?
Well, we mentioned the term space complexity a lot of times when talking about Time Complexity. Space complexity refers to the amount of storage required by the program/algorithm including the amount of space required by each variable.
However, people often get confused about space complexity with the term auxiliary space. Auxiliary space is just the temporary or extra space required by the algorithm.
Space Complexity = memory required by variable + extra space
A good algorithm should have low space complexity as it will then also affect its running time.
Relation Between Time And Space Complexity
The trade-offs between time and space complexity are often inversely proportional, meaning that improving one may worsen the other. For example, a hash table is a data structure that can perform insertions, deletions, and searches in constant time, O(1), regardless of the input size. However, a hash table also requires a lot of memory to store the data and avoid collisions, which are situations where two different keys map to the same index in the table.
A linked list, on the other hand, is a data structure that can perform insertions and deletions in constant time, O(1), but requires linear time, O(n), to search for an element. A linked list also requires less memory than a hash table, as it only stores the data and a pointer to the next node.
Conclusion
The concept of time complexity refers to the quantification of the length of time it takes a set of instructions/ algorithm to process or run as just a function of the total quantity of data that is fed into the system. To put it another way, time complexity refers to a native program function's efficiency as well as the amount of time it takes for the function to process a certain input. The quantity of memory that an algorithm requires to carry out its instructions and generate the desired output is referred to as its "space complexity".
You may also like to read:
- 50 Software Testing Interview Questions And Answers You Should Know!
- 51 Competitive Coding Questions (With Solutions) - Do NOT Skip These!
- List Of 50 Core Java Interview Questions With Answers (2022)
- Top 50 .NET Core Interview Questions And Answers 2022
- Linux Kernel, In A Nutshell, To Help You Prepare For Linux Interview Questions
As a biotechnologist-turned-writer, I love turning complex ideas into meaningful stories that inform and inspire. Outside of writing, I enjoy cooking, reading, and travelling, each giving me fresh perspectives and inspiration for my work.
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter














Comments
Add comment