- What Is Recursion In Python Programming?
- Importance Of Recursion In Python Programming
- How Does Factorial Recursion Work?
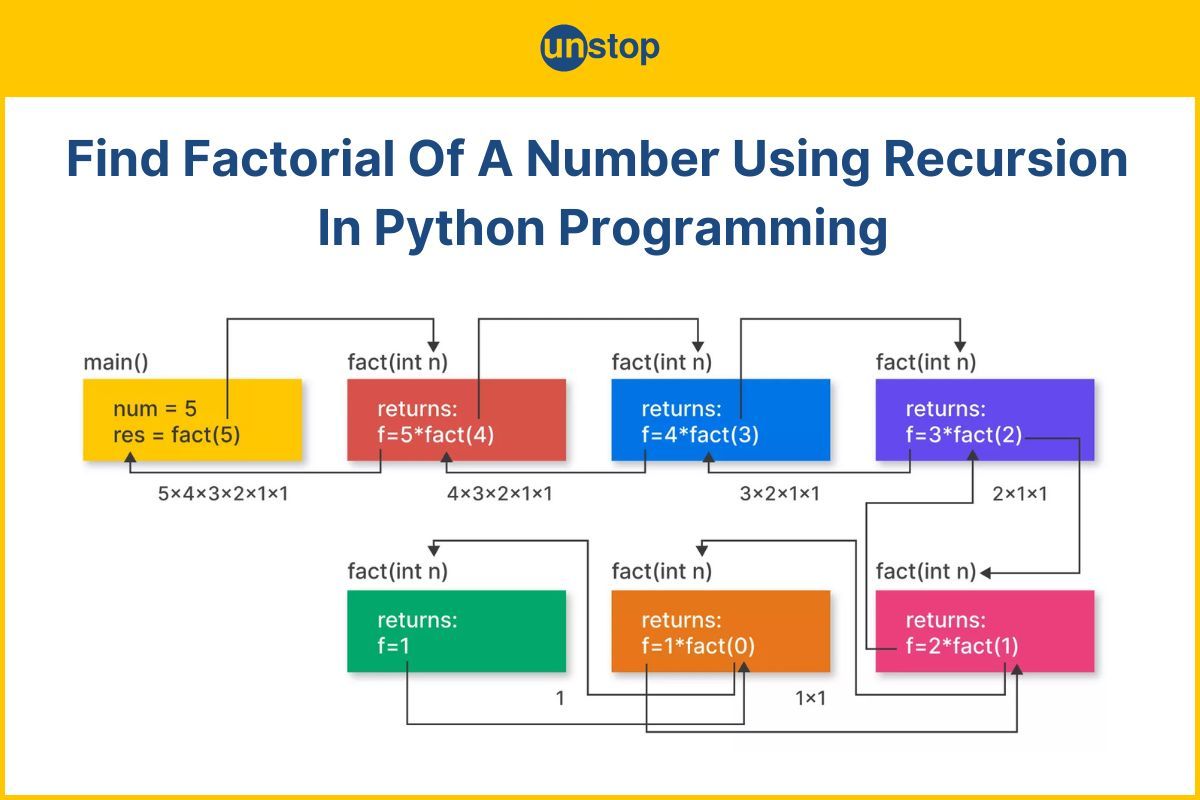
- Working Mechanism To Find Factorial Using Recursion In Python
- Python Program To Find Factorial Of A Number Using Recursion
- Python Program To Display An Error Message If A User Input Negative Number
- Limitations Of Using Recursion To Find Factorial Of A Number In Python
- Conclusion
- Frequently Asked Questions
Find Factorial Of A Number Using Recursion In Python Programming
Factorials are everywhere in math and computer science—whether you're working with probabilities, permutations, or even analyzing algorithms. But what exactly is a factorial, and how can we calculate it in Python? In this article, we'll explore a cool way to find factorials using a technique called recursion.
Recursion lets a function call itself to solve smaller pieces of a problem until it reaches a solution. Don't worry if that sounds a bit complex right now—we'll break it down step-by-step and show you how simple it can actually be! Plus, you’ll get some practice with Python functions and recursion concepts that are super useful for coding assignments and real-world applications.
What Is Recursion In Python Programming?
Recursion in Python programming is when a function calls itself to solve a problem by breaking it down into smaller, similar problems. Think of it as a loop, but instead of repeating code, the function calls itself until it reaches a stopping point, known as the base case.
Real-World Example: Nested Boxes
Imagine you have a set of boxes inside each other, like Russian nesting dolls. Each box contains a slightly smaller box until you reach the tiniest one with nothing inside. To find the smallest box, you would open each box in sequence, taking out the next one until you reach the smallest box.
In this scenario, each box-opening is a step in a recursive process, where:
- Each step is the same action: opening a box.
- You continue until the base case—when you find the smallest box.
Recursion in programming languages works similarly. You solve a small piece of the problem (opening one box), then call the function again to repeat the action until the base case is reached.
A base case serves as a crucial stopping point for the function. It prevents the function from calling itself infinitely, which would lead to problems such as infinite loops or stack overflow.
Importance Of Recursion In Python Programming
Recursion really shines when you use it to clean up code for complex, confusing algorithms. Here’s why recursion is important in Python:
- Simplifies Code for Complex Problems: Recursion is invaluable for problems that have a naturally recursive structure, like mathematical sequences (factorials, Fibonacci numbers), or tree and graph traversals. It often leads to cleaner and more readable code as it mirrors the problem’s structure directly.
- Reduces the Need for Loops: Recursive solutions can replace complex nested loops with a function that repeatedly calls itself until a condition is met. This is especially helpful in handling tasks like searching through nested directories or processing hierarchical data structures, which would otherwise require intricate looping.
- Improves Modularity: Recursive functions allow complex problems to be broken down into manageable parts, each solved by a simpler function call. This modularity makes it easier to understand, test, and maintain code.
- Enables Efficient Algorithms: In certain cases, recursive algorithms can be more efficient than their iterative counterparts. For example, quicksort and mergesort use recursion to achieve optimal sorting times, reducing time complexity in comparison to basic sorting techniques.
- Supports Backtracking Solutions: Recursive functions are crucial in problems where backtracking is involved, such as puzzles, mazes, and other combinatorial problems. By calling itself with different parameter values, recursion enables exploring all possible solutions in a structured manner.
- Enhances Code Readability: Recursion often provides a more intuitive approach for solving problems by reducing lines of code and making the logic behind the code easier to follow, particularly for problems that are inherently recursive.
Explore this amazing course and master all the key concepts of Python programming effortlessly!
How Does Factorial Recursion Work?
When we're speaking about factorials, we're actually talking about this mystical thing in mathematics. The factorial of a number is written as (n!). It’s the product of all positive integers from that number down to 1.
- For example, the factorial of 5, written as 5!, equals 5 × 4 × 3 × 2 × 1, which results in 120.
- Factorials are important in fields like combinatorics and probability, where they help us count arrangements or selections of items.
- So, whether you’re calculating probabilities or exploring permutations, understanding factorials is key.
Let’s look at some examples to see how this works.
- 1 is 1 (the factorial of one is just one).
- 2! = 2 x 1 = 2
- 3! = 3 x 2 x 1 = 6
- 4! = 4 x 3 x 2 x 1 = 24
It’s important to note that factorials are not defined for negative numbers, and by convention, 0! is equal to 1. This property of 0! = 1 might seem odd, but it's essential in mathematics to keep formulas consistent.
Role Of Recursion In Factorial Calculation
Recursion provides an elegant way to calculate factorials. In recursion, a function calls itself with a smaller version of the problem until it reaches a base case. This approach often leads to cleaner and more readable code.
For factorials, the recursive formula is straightforward:
(n! = n × (n-1)!).
To find the factorial of any number n, you multiply n by the factorial of (n - 1), continuing until you reach the base case of 0!, which is defined as 1.
This method not only simplifies the computation but also aligns perfectly with how factorials are mathematically defined.
Working Mechanism To Find Factorial Using Recursion In Python
To find the factorial of a number using recursion in Python, here’s a step-by-step breakdown of how it works:

Step 1: Define the Recursive Function
- Create a function that takes a number n as input. This function will call itself to compute the factorial of n until it reaches the base case.
Step 2: Set Up the Base Case
- In recursion, the base case is critical as it prevents infinite loops.
- For factorial, the base case is when n = 0 or n=1. By definition, 0!=1 and 1!=1. So, if n is 0 or 1, the function should return 1.
Step 3: Implement the Recursive Case
- If n is greater than 1, the function should call itself with n - 1 and multiply the result by n.
- This step is based on the mathematical formula for factorial: n!=n×(n−1)!.
Step 4: Recursive Calls Proceed Until the Base Case
- Each recursive call reduces n by 1, so eventually, n will reach 1 (or 0), where the base case is met.
- At this point, the recursion stops, and the function starts returning values back up the chain of recursive calls.
Step 5: Multiply and Return Results Back Up the Call Stack
- Each level of the recursion multiplies n by the result of (n−1)! calculated in the next recursive call.
- When the base case returns 1, the multiplications unwind back up, ultimately providing the factorial of the original n.
Sharpen your coding skills with Unstop's 100-Day Coding Sprint and compete now for a top spot on the leaderboard!
Python Program To Find Factorial Of A Number Using Recursion
Here’s a simple Python program to find the factorial of a number using recursion-
Code Example:
def factorial(n):
# Base case: if n is 0 or 1, return 1
if n == 0 or n == 1:
return 1
# Recursive case: multiply n by the factorial of (n-1)
else:
return n * factorial(n - 1)
# Take user input
number = int(input("Enter a number to find its factorial: "))
# Call the factorial function and print the result
print(f"The factorial of {number} is {factorial(number)}")
ZGVmIGZhY3RvcmlhbChuKToKICAgICMgQmFzZSBjYXNlOiBpZiBuIGlzIDAgb3IgMSwgcmV0dXJuIDEKICAgIGlmIG4gPT0gMCBvciBuID09IDE6CiAgICAgICAgcmV0dXJuIDEKICAgICMgUmVjdXJzaXZlIGNhc2U6IG11bHRpcGx5IG4gYnkgdGhlIGZhY3RvcmlhbCBvZiAobi0xKQogICAgZWxzZToKICAgICAgICByZXR1cm4gbiAqIGZhY3RvcmlhbChuIC0gMSkKCiMgVGFrZSB1c2VyIGlucHV0Cm51bWJlciA9IGludChpbnB1dCgiRW50ZXIgYSBudW1iZXIgdG8gZmluZCBpdHMgZmFjdG9yaWFsOiAiKSkKCiMgQ2FsbCB0aGUgZmFjdG9yaWFsIGZ1bmN0aW9uIGFuZCBwcmludCB0aGUgcmVzdWx0CnByaW50KGYiVGhlIGZhY3RvcmlhbCBvZiB7bnVtYmVyfSBpcyB7ZmFjdG9yaWFsKG51bWJlcil9IikK
Output:
Enter a number: 8
The factorial of 8 is 40320
Explanation:
In the above code example-
- We define a recursive function called factorial that calculates the factorial of a given integer n.
- Base Case: Inside the function, we check if n is 0 or 1. If it is, we return 1, because the factorial of both 0 and 1 is defined as 1. This serves as the stopping condition for the recursion.
- Recursive Case: If n is greater than 1, we return n * factorial(n - 1). This means we multiply n by the result of calling the factorial function with n - 1. The function continues to call itself with decreasing values of n, building up the factorial result step by step until the base case is reached.
- We then prompt the user to enter a number and convert the input to an integer, storing it in the variable number.
- Finally, we call the factorial function with the value of number and print the result, displaying the factorial of the entered number.
Python Program To Display An Error Message If A User Input Negative Number
To display an error message when the user inputs a negative number in the factorial program, we’ll add a check right after taking input. If the input is negative, the program will print an error message and stop further execution. Here’s how it can be done-
Code Example:
# Recursive function to calculate factorial
def factorial(n):
# Base case: if n is 0 or 1
if n == 0 or n == 1:
return 1
# Recursive case
else:
return n * factorial(n - 1)
# Taking input from the user
number = int(input("Enter a number: "))
# Checking if the input is valid
if number < 0:
print("Error: Factorial is not defined for negative numbers.")
else:
# Calculating and displaying the factorial
print(f"The factorial of {number} is {factorial(number)}")
IyBSZWN1cnNpdmUgZnVuY3Rpb24gdG8gY2FsY3VsYXRlIGZhY3RvcmlhbApkZWYgZmFjdG9yaWFsKG4pOgogICAgIyBCYXNlIGNhc2U6IGlmIG4gaXMgMCBvciAxCiAgICBpZiBuID09IDAgb3IgbiA9PSAxOgogICAgICAgIHJldHVybiAxCiAgICAjIFJlY3Vyc2l2ZSBjYXNlCiAgICBlbHNlOgogICAgICAgIHJldHVybiBuICogZmFjdG9yaWFsKG4gLSAxKQoKIyBUYWtpbmcgaW5wdXQgZnJvbSB0aGUgdXNlcgpudW1iZXIgPSBpbnQoaW5wdXQoIkVudGVyIGEgbnVtYmVyOiAiKSkKCiMgQ2hlY2tpbmcgaWYgdGhlIGlucHV0IGlzIHZhbGlkCmlmIG51bWJlciA8IDA6CiAgICBwcmludCgiRXJyb3I6IEZhY3RvcmlhbCBpcyBub3QgZGVmaW5lZCBmb3IgbmVnYXRpdmUgbnVtYmVycy4iKQplbHNlOgogICAgIyBDYWxjdWxhdGluZyBhbmQgZGlzcGxheWluZyB0aGUgZmFjdG9yaWFsCiAgICBwcmludChmIlRoZSBmYWN0b3JpYWwgb2Yge251bWJlcn0gaXMge2ZhY3RvcmlhbChudW1iZXIpfSIpCg==
Output:
Enter a number: -6
Error: Factorial is not defined for negative numbers.
Explanation:
In the above code example-
- We define a function factorial that calculates the factorial of a given number n using recursion.
- Base Case: Inside the function, we check if n is 0 or 1. If so, we return 1, since the factorial of 0 and 1 is defined as 1. This base case helps stop the recursion.
- Recursive Case: If n is greater than 1, we return n * factorial(n - 1). Here, the function calls itself with n - 1 as the argument. This process continues, with each recursive call reducing n by 1, until we reach the base case.
- We prompt the user to enter a number, which we convert to an integer and store as number.
- Input Validation: Before proceeding, we check if the entered number is negative. If number is less than zero, we print a message stating that the factorial is not defined for negative numbers.
- If number is non-negative, we call the factorial function with number and store the result.
- Finally, we print the factorial result, formatted to display the entered number and its calculated factorial value.
Limitations Of Using Recursion To Find Factorial Of A Number In Python
When using recursion to find the factorial of a number in Python, there are some common errors and issues that students and developers might encounter. Here are a few along with troubleshooting tips to resolve them:
1. RecursionError: Maximum Recursion Depth Exceeded
- Issue: Python sets a limit on the number of recursive calls to prevent infinite recursion and stack overflow. If the number is too large (e.g., 1000 or more), the recursion depth may exceed Python’s limit.
- Solution: For large numbers, consider using an iterative approach instead of recursion, or increase the recursion depth limit (not generally recommended) with sys.setrecursionlimit(). For instance:
import sys
sys.setrecursionlimit(2000) # Adjust based on your needs
2. Negative Input Handling
- Issue: Factorials are not defined for negative numbers, but if a negative number is passed to the recursive function, it could lead to infinite recursion or incorrect output.
- Solution: Before calling the factorial function, check if the input is negative. If it is, display an error message and avoid calling the function.
if number < 0:
print("Error: Factorial is not defined for negative numbers.")
else:
print(f"The factorial of {number} is {factorial(number)}")
3. Stack Overflow (Memory Issue)
- Issue: Recursion uses the call stack, and for very large inputs, the stack can overflow due to excessive recursive calls, causing the program to crash.
- Solution: For larger values, switch to an iterative approach, which avoids recursive calls and the risk of stack overflow.
4. Missing Base Case
- Issue: If the base case (n == 0 or n == 1) is not included in the recursive function, it will continue calling itself indefinitely, eventually leading to a RecursionError.
- Solution: Ensure the base case is properly defined. The factorial function should have a base case that returns 1 when n is 0 or 1:
if n == 0 or n == 1:
return 1
5. Syntax Errors And Typographical Mistakes
- Issue: Common syntax errors, such as missing colons, incorrect indentation, or misspelled function names, can lead to errors in Python.
- Solution: Double-check syntax, ensure proper indentation, and verify function names.
SyntaxError: invalid syntax
6. Passing Non-Integer Values
- Issue: If a non-integer value (like a float or string) is passed, the recursive function will fail because it expects integers.
- Solution: Check that the input is a non-negative integer before calling the factorial function. You can add input validation as follows:
if not isinstance(number, int) or number < 0:
print("Error: Please enter a non-negative integer.")
else:
print(f"The factorial of {number} is {factorial(number)}")
Conclusion
Finding the factorial of a number using recursion is a powerful example of how recursion can simplify complex mathematical calculations. By breaking the problem down into smaller, repetitive steps, recursion enables us to compute factorials with clean and concise code. While recursion is elegant and intuitive, especially for smaller numbers, it's essential to be mindful of potential pitfalls like excessive memory usage and stack overflow for larger inputs.
For efficiency in large-scale applications, exploring optimization techniques, such as memoization or iterative solutions, can be valuable. With these insights, you now have a solid foundation for using recursion to calculate factorials and apply similar techniques to other recursive problems in Python.
Searching for someone to answer your programming-related queries? Find the perfect mentor here.
Frequently Asked Questions
Q. What is recursion in programming?
Recursion is a programming technique that allows you to define a function that calls itself to solve a problem in a more manageable way. It’s commonly utilized for tasks such as factorial calculations, data structure traversals, and more.
Q. Can recursion be replaced with iteration?
Yes, recursion can often be replaced with iteration, though it depends on the problem. Many recursive problems can be solved iteratively, especially those with a simple recursive structure, like calculating factorials, Fibonacci numbers, or performing basic traversals.
For instance, the factorial function can be easily converted into an iterative loop, which avoids the overhead of recursive function calls and stack usage:
Q. What is the time complexity of recursive factorial?
The time complexity of calculating the factorial of a number using recursion is O(n). This is because the function calls itself n times, decreasing the number by 1 with each call, until it reaches the base case of n = 0 or n = 1. Therefore, the recursive factorial function has a linear time complexity with respect to n.
Q. Is recursion always the best approach?
Recursion isn’t always the best approach. While it can simplify problems like calculating factorials, traversing trees, or solving problems with a naturally recursive structure, recursion has trade-offs. Here are some key points to consider:
When Recursion Is Beneficial
- Simplifies Code: Recursive solutions often lead to cleaner, shorter, and more readable code, especially for problems like tree traversal or factorial calculation.
- Follows Natural Problem Structure: For problems that naturally break down into smaller subproblems (like the Fibonacci sequence or quicksort), recursion can feel intuitive and align well with the problem’s structure.
When Recursion Is Not Ideal
- Stack Overflow: Each recursive call takes up stack memory, so if there are too many calls (e.g., for large values of n in factorial), it can lead to a stack overflow error.
- Higher Memory Usage: Recursive functions use the call stack to store intermediate states, which can consume more memory compared to iterative solutions.
- Performance Limitations: In languages that don’t optimize tail recursion, recursion can be slower than iteration due to function call overhead.
Q. What are some common errors with recursive functions?
Common errors with recursive functions often stem from issues with the base case, excessive memory use, or unintended infinite loops. A missing or incorrect base case is a frequent mistake that can cause the recursion to run indefinitely, eventually leading to a stack overflow or RecursionError in Python. Stack overflow occurs when the recursion depth becomes too large, as each recursive call consumes additional stack memory.
Another issue is inefficient recursion, where the same subproblems are recalculated multiple times (e.g., naive Fibonacci recursion), leading to redundant computations and slow performance. Incorrect parameter adjustments between recursive calls can also cause errors, resulting in unexpected or incorrect outputs.
Q. How can I optimize my recursive functions?
Optimizing recursive functions can help reduce time complexity, memory usage, and prevent stack overflow errors. Here are some effective techniques:
-
Memoization: Cache the results of recursive calls to avoid redundant calculations.
-
Best for: Overlapping subproblems, like Fibonacci or dynamic programming problems.
-
-
Limit Recursive Depth: Avoid deep recursion by using iteration or increasing Python’s recursion limit with caution.
-
Best for: Functions with high recursion depth.
-
-
Tail Recursion: Use tail recursion to streamline calls, though Python doesn’t natively optimize it.
-
Best for: Situations where recursion can be written in a tail-recursive form, simplifying iterative conversion.
-
-
Convert to Iteration: Rewrite the recursive function as an iterative loop when possible.
-
Best for: Simple recursive calculations, like factorials or Fibonacci.
-
-
Bottom-Up Dynamic Programming: Use an iterative, bottom-up approach to solve subproblems.
-
Best for: Problems where each solution builds from previous subproblems, like coin change or Fibonacci.
-
-
Use Stack Data Structures: Simulate recursion using an explicit stack for control over recursive behavior.
-
Best for: Complex recursive problems, such as depth-first search (DFS) in graph traversal.
-
Each of these strategies can make recursive functions more efficient, especially for larger inputs.
With this, we conclude our discussion on how to find the factorial of a number using recursion in Python programming language. Here are a few other topics that you might be interested in reading:
- 12 Ways To Compare Strings In Python Explained (With Examples)
- Python Logical Operators, Short-Circuiting & More (With Examples)
- Python Bitwise Operators | Positive & Negative Numbers (+Examples)
- Python String.Replace() And 8 Other Ways Explained (+Examples)
- How To Reverse A String In Python? 10 Easy Ways With Examples!
I’m a Computer Science graduate with a knack for creative ventures. Through content at Unstop, I am trying to simplify complex tech concepts and make them fun. When I’m not decoding tech jargon, you’ll find me indulging in great food and then burning it out at the gym.
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter















Comments
Add comment