- What Is Array Sorting In C++?
- Types Of Sorting Techniques In C++
- How To Sort Array In C++ Using sort() Function?
- How To Sort Array In C++ Using qsort() Function?
- How To Sort Array In C++ Using Bubble Sort?
- How To Sort Array In C++ Using Insertion Sort?
- How To Sort An Array In C++ Using Selection Sort?
- How To Sort An Array In C++ Using Quicksort?
- How To Sort Array In C++ Using Merge Sort?
- How To Sort Data in C++ With Custom Function?
- Partial Sort Function To Sort An Array In C++
- Complexity Analysis
- Conclusion
- Frequently Asked Questions
9 Ways To Sort Array In C++ (A Detailed Guide With Code Examples)

An array is a collection of the same data type elements stored in contiguous memory locations, that can be retrieved using a common identifier or index. They are used to save and manage collections of data, which include a list of numbers, a sequence of characters, or a set of objects. They are regularly used in programming languages for various purposes, including storing data, sorting and searching algorithms, and mathematical calculations.
In this article, we will discuss how to sort an array in C++ programming. It is one of the most important aspects of working with an array especially if we are dealing with large quantities of data.
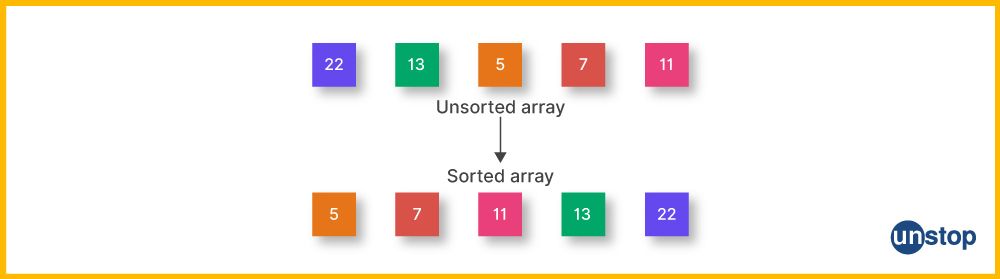
What Is Array Sorting In C++?
As we've mentioned above, arrays are a collection of data with elements belonging to a single data type. These may be one-dimensional, two-dimensional, or multidimensional, depending on the number of indices required. One-dimensional arrays are regularly known as vectors, while two-dimensional arrays are occasionally referred to as matrices. Now, let's see what sorting an array is all about!
Sorting an array in C++ language entails arranging its elements in a particular sequence. This process is useful in various applications, including data analysis, searching, and data processing. Essentially, sorting an array permits programmers to manage large quantities of information more accurately. This makes it easier to search for particular data, perform calculations, and access data.
In C++, sorting may be classified into two categories, i.e., internal sorting and external sorting.
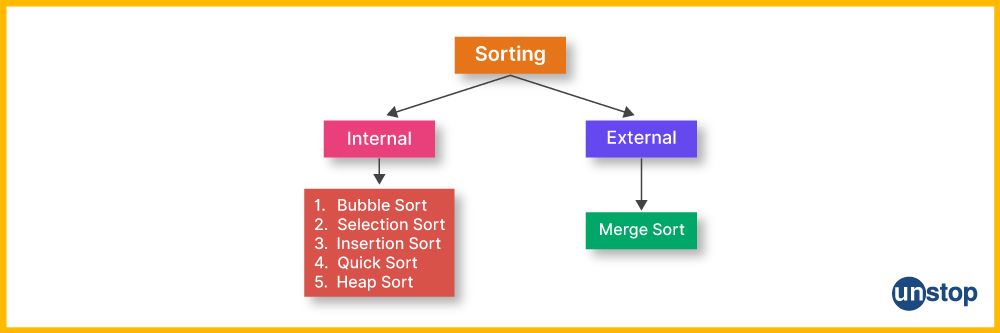
Internal sorting: Internal sorting is the method of sorting data that resides entirely within the computer's primary memory (RAM), as opposed to utilizing external storage devices like hard drives or solid-state drives. Internal sorting is the preferred approach for sorting small to medium-sized datasets due to the considerable speed advantage of accessing data from RAM compared to external storage devices.
External sorting: C++ employs external sorting techniques when working with big data sets that cannot fit into a computer's memory (RAM). This involves breaking down the data into smaller parts that can fit into memory space and applying internal sorting methods such as quicksort, mergesort, or heapsort on each chunk. Once each small part is sorted, they are merged to produce the final sorted output.
Types Of Sorting Techniques In C++
C++ provides several built-in function and algorithms for sorting arrays, including:
- sort(): C++ has a sort() function that comes pre-built in the algorithm library. This function sorts an array's elements in ascending order as the default behavior.
- qsort(): This function is a part of the C standard library but can be utilized to sort the elements of an array in C++, in ascending order. The sorting criteria are determined by a custom comparison function specified by the programmer.
- Bubble sort: Bubble sort is a user-defined, simple sorting algorithm that repeatedly compares and swaps adjacent elements if they are in the wrong order until the array is sorted.
- Insertion sort: This is another easy user-defined sorting algorithm that builds a sorted array of one element at a time by inserting each element into its correct position relative to the previously sorted elements.
- Selection sort: Selection sort is also a user-defined sorting algorithm that sorts an array by repeatedly locating the minimum element from the unsorted part of the array and putting it at the beginning of the sorted part.
- Quick Sort: This user-defined sorting algorithm is based on the divide-and-conquer method. It begins by selecting a pivot element from the input array. The remaining elements in the array are then partitioned into sub-arrays primarily based on whether they're less than or more than the pivot element. The algorithm recursively sorts the two sub-arrays using the same approach until all of the sub-arrays are sorted. Finally, the sub-arrays are merged to provide the final sorted array.
- Merge Sort: This algorithm is a variation on divide-and-conquer as it divides the unsorted array into n sub-arrays, each of which has one element, then continually merges the sub-arrays to create new sorted subarrays until there is only one sub-array left. It is typically implemented as a user-defined function.
Now, let's look at all these techniques in greater detail, along with proper code examples for each.
How To Sort Array In C++ Using sort() Function?
The sort() function is an integrated feature of the C++ Standard Library and is specified within the <algorithm> header. This function can be used to sort an array's elements either in ascending or descending order. Note that, in C++, the sort() function does not return anything, meaning it has a return type of void.
Syntax:
sort(start_address, end_address, optional_compare_function);
Here,
- start_address, end_address: The address of the range's first and last elements that need to be sorted.
- optional_compare_function: An optional parameter which specifies how to compare two elements and decide the order. If not provided, the default less-than operator(<) is used for comparison.
Code Example:
#include
#include
using namespace std;
int main() {
int arr[] = {3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5};
int n = sizeof(arr) / sizeof(arr[0]);
// Sort the array in ascending order
sort(arr, arr + n);
cout << "Sorted array in ascending order: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgojaW5jbHVkZSA8YWxnb3JpdGhtPgoKdXNpbmcgbmFtZXNwYWNlIHN0ZDsKCmludCBtYWluKCkgewppbnQgYXJyW10gPSB7MywgMSwgNCwgMSwgNSwgOSwgMiwgNiwgNSwgMywgNX07CmludCBuID0gc2l6ZW9mKGFycikgLyBzaXplb2YoYXJyWzBdKTsKCi8vIFNvcnQgdGhlIGFycmF5IGluIGFzY2VuZGluZyBvcmRlcgpzb3J0KGFyciwgYXJyICsgbik7Cgpjb3V0IDw8ICJTb3J0ZWQgYXJyYXkgaW4gYXNjZW5kaW5nIG9yZGVyOiAiOwpmb3IgKGludCBpID0gMDsgaSA8IG47IGkrKykgewpjb3V0IDw8IGFycltpXSA8PCAiICI7Cn0KY291dCA8PCBlbmRsOwoKcmV0dXJuIDA7Cn0=
Output:
Sorted array in ascending order: 1 1 2 3 3 4 5 5 5 6 9
Explanation:
This C++ program example explains how to sort an array of integers in ascending order using the sort function from the algorithm library in C++.
- We begin by including necessary header files <iostream> for input/output operations and <algorithm> for the sort() function, along with the namespace to use standard C++ names.
- Inside the main() function, we initialize an integer array called arr with the values {3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5}.
- Then, we calculated the size of the array using the sizeof() operator, i.e., dividing the total size of the array (sizeof(arr)) by the size of a single element (sizeof(arr[0])) and storing it in the integer variable n. Thus, the value of n will be 11 in this instance because the array contains 11 elements.
- Next, we sort the elements of the array arr in ascending order using the sort() function.
- For this, we pass arr as the starting memory address of the array and arr+n as the ending memory address of the array.
- The sort() function arranges these elements in ascending order by default.
- After sorting, we print the array to the console using the cout command and a for loop. The loop iterates over each element till condition i<n holds true while incrementing 'i' after every iteration.
- Lastly, the main() function ends with a return 0 statement indicating successful execution.
Time Complexity: The time complexity of the sort function is O(n log n).
Space Complexity: The space complexity of the sort function is O(log n).
To read more: Sort() Function In C++ & Algorithms Explained (+Code Examples)
How To Sort Array In C++ Using qsort() Function?
As mentioned before, the qsort() function is inherited from the C standard library <cstblib> and can be used to sort an array in C++ programs.
- The function accepts a base pointer to the array, the number of elements in it, the size of each element and a comparison function.
- The comparison function returns an integer to indicate the relative ordering of two elements being compared (i.e., sorting order).
- The function's return type is void as it directly modifies the array.
Syntax:
void qsort(void* base, size_t num, size_t size, int (*compar)(const void*,const void*));
Here,
- void* base refers to the base pointer, which is the first element of the array to be sorted.
- num is the number of elements in the array, while size is the size of each element in bytes.
- *compar is a pointer to a comparison function that acquires two const void* parameters and returns an int (integer) indicating the order of the elements.
Code Example:
#include
#include
int ascending(const void* x, const void* t) {
return (*(int*)x - *(int*)t);
}
int main() {
const int n = 9;
int values[n] = {71, 58, 99, 7, 13, 85, 68, 21, 38};
std::cout << "Before sorting the array: ";
for (int i = 0; i < n; ++i) {
std::cout << values[i] << " ";
}
std::cout << std::endl;
// Sort the array using qsort with the ascending comparator
qsort(values, n, sizeof(int), ascending);
std::cout << "After sorting the array in ascending order: ";
for (int i = 0; i < n; ++i) {
std::cout << values[i] << " ";
}
std::cout << std::endl;
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgojaW5jbHVkZSA8Y3N0ZGxpYj4KCmludCBhc2NlbmRpbmcoY29uc3Qgdm9pZCogeCwgY29uc3Qgdm9pZCogdCkgewpyZXR1cm4gKCooaW50Kil4IC0gKihpbnQqKXQpOwp9CgppbnQgbWFpbigpIHsKY29uc3QgaW50IG4gPSA5OwppbnQgdmFsdWVzW25dID0gezcxLCA1OCwgOTksIDcsIDEzLCA4NSwgNjgsIDIxLCAzOH07CgpzdGQ6OmNvdXQgPDwgIkJlZm9yZSBzb3J0aW5nIHRoZSBhcnJheTogIjsKZm9yIChpbnQgaSA9IDA7IGkgPCBuOyArK2kpIHsKc3RkOjpjb3V0IDw8IHZhbHVlc1tpXSA8PCAiICI7Cn0Kc3RkOjpjb3V0IDw8IHN0ZDo6ZW5kbDsKCi8vIFNvcnQgdGhlIGFycmF5IHVzaW5nIHFzb3J0IHdpdGggdGhlIGFzY2VuZGluZyBjb21wYXJhdG9yCnFzb3J0KHZhbHVlcywgbiwgc2l6ZW9mKGludCksIGFzY2VuZGluZyk7CgpzdGQ6OmNvdXQgPDwgIkFmdGVyIHNvcnRpbmcgdGhlIGFycmF5IGluIGFzY2VuZGluZyBvcmRlcjogIjsKZm9yIChpbnQgaSA9IDA7IGkgPCBuOyArK2kpIHsKc3RkOjpjb3V0IDw8IHZhbHVlc1tpXSA8PCAiICI7Cn0Kc3RkOjpjb3V0IDw8IHN0ZDo6ZW5kbDsKCnJldHVybiAwOwp9
Output:
Before sorting the array: 71 58 99 7 13 85 68 21 38
After sorting the array in ascending order: 7 13 21 38 58 68 71 85 99
Explanation:
In the C++ program example, we first include the <iostream> and <cstdlib> C++ libraries for input/output functions and the qsort() function, respectively.
- We then define an ascending() function (i.e., a comparison function) to compare two integers and determine the order of elements during sorting.
- This function takes two const void* parameters, x and t, which are generic pointers that doesn’t specify what kind of data it points to.
- Inside the function, we first typecast the pointers to int type (using casting operator) and then use the dereference operator to access the values being pointed to.
- Next, we use the subtraction arithmetic operator to deduct the integer value pointed to by t, from the value pointed to by x. The return value determines the order of sorting.
- Here, negative number indicates value pointed to by x is less than value pointed to by t, which is opposite for a positive number. Also, a zero indicates both values are equal.
- Inside the main() function, we first declare a constant integer variable n and initialize it with 9.
- We also declare an integer array called values, with the size of n (i.e., 9), and initialize it with values {71, 58, 99, 7, 13, 85, 68, 21, 38}.
- Then, using the cout command and a for loop, we iterate through each element of the array and print the unsorted array to the console.
- Next, we call the qsort() function to sort the values array in ascending order.
- The qsort() function takes four arguments: the array to sort (values), the number of elements(n), the size of each element(sizeof(int)), and the comparison function(ascending).
- After the function sorts the array, we print the sorted array using another for loop to show the result after sorting. Each element is output followed by a space.
Time Complexity: The time complexity of the qsort() function is O(n log n). However, the worst-case time complexity can be O(n^2).
Space Complexity: The space complexity of the qsort() function is O(log n).
How To Sort Array In C++ Using Bubble Sort?
Bubble sort is a simple yet efficient sorting algorithm used in the C++ language. It iteratively moves through an array to compare nearby elements and swaps them if they are in the wrong order. The process is repeated until the array is sorted.
Here is what happens when you sort an array in C++ using bubble sort-
- We start by comparing the first pair of elements. If the first element is greater than the second, we swap them.
- We then move to the following pair of elements, repeat this comparison, and switch processes until we reach the end of the array.
- The whole process repeats for n-1 passes, in which n is the overall quantity of elements inside the array. Each pass places the next largest element in its correct position.
- Once we have finished all n-1 passes, the array will be sorted in ascending order.
The Bubble Sort algorithm in C++ has the following syntax:
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// swap arr[j] and arr[j+1]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;}
}
}
}
Here,
- The integer array arr[] and number of elements/ array size n (integer variable) are the two parameters that the bubbleSort() function accepts.
- The for keywords mark the nested for loops, where the outer loop controls the number of passes, and the inner loop compares and swaps adjacent elements.
- The integer variable temp is the temporary variable used to perform the swap.
Code Example:
#include
using namespace std;
void bubbleSort(int arr[], int n) {
bool swapped = true;
while (swapped) {
swapped = false;
// Perform a pass through the array
for (int i = 0; i < n - 1; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr[i], arr[i + 1]);
swapped = true;
}
}
// Reduce the range of the next pass
n--;
}
}
int main() {
int arr[] = {5, 3, 8, 6, 7, 2};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Before sorting: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
// Sort the array using bubble sort
bubbleSort(arr, n);
cout << "After sorting: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgoKdXNpbmcgbmFtZXNwYWNlIHN0ZDsKCnZvaWQgYnViYmxlU29ydChpbnQgYXJyW10sIGludCBuKSB7CmJvb2wgc3dhcHBlZCA9IHRydWU7Cgp3aGlsZSAoc3dhcHBlZCkgewpzd2FwcGVkID0gZmFsc2U7CgovLyBQZXJmb3JtIGEgcGFzcyB0aHJvdWdoIHRoZSBhcnJheQpmb3IgKGludCBpID0gMDsgaSA8IG4gLSAxOyBpKyspIHsKaWYgKGFycltpXSA+IGFycltpICsgMV0pIHsKc3dhcChhcnJbaV0sIGFycltpICsgMV0pOwpzd2FwcGVkID0gdHJ1ZTsKfQp9CgovLyBSZWR1Y2UgdGhlIHJhbmdlIG9mIHRoZSBuZXh0IHBhc3MKbi0tOwp9Cn0KCmludCBtYWluKCkgewppbnQgYXJyW10gPSB7NSwgMywgOCwgNiwgNywgMn07CmludCBuID0gc2l6ZW9mKGFycikgLyBzaXplb2YoYXJyWzBdKTsKCmNvdXQgPDwgIkJlZm9yZSBzb3J0aW5nOiAiOwpmb3IgKGludCBpID0gMDsgaSA8IG47IGkrKykgewpjb3V0IDw8IGFycltpXSA8PCAiICI7Cn0KY291dCA8PCBlbmRsOwoKLy8gU29ydCB0aGUgYXJyYXkgdXNpbmcgYnViYmxlIHNvcnQKYnViYmxlU29ydChhcnIsIG4pOwoKY291dCA8PCAiQWZ0ZXIgc29ydGluZzogIjsKZm9yIChpbnQgaSA9IDA7IGkgPCBuOyBpKyspIHsKY291dCA8PCBhcnJbaV0gPDwgIiAiOwp9CmNvdXQgPDwgZW5kbDsKCnJldHVybiAwOwp9
Output:
Before sorting: 5 3 8 6 7 2
After sorting: 2 3 5 6 7 8
Explanation:
The bubble sort algorithm is shown in the code above indicating how to sort an array in C++, in ascending order.
- We define a bubbleSort() function, which takes two parameters, arr (an integer array) and integer n (i.e., the array's size).
- Inside the function, we declare a boolean variable/ flag called swapped and initialize it to the boolean value true. This variable will be used to track whether any swaps were made during each pass of the array.
- We then enter a while loop that will continue executing as long as variable swapped is true.
- At the beginning of each iteration, we set the value of swapped variable to false to track if any swaps occur during this pass.
- Then, we use a for loop with an if-statement nested inside it. The loop iterates from first to second to last element (i = 0 to i < n-1), comparing the current element with the next element in the array and performing swaps if they are found to be in an incorrect order.
- If the current element (arr[i]) is greater than the one following it (arr[i + 1]), we swap the two elements and assign the value true to swapped variable. This process ensures that the largest unsorted element bubbles up to its correct position at the end of the array.
- After the for loop completes iterations, we decrement the value of n, to reduce the range of the next pass by 1. This is because the last element in the current range is already sorted.
- Once all the array elements are sorted and there are no more values to be swapped in a pass, the value of swapped variable will become false. As a result, the while loop will terminate, indicating that the array is sorted.
- In the main() function, we declare an integer array, arr, and initialize it with values {5, 3, 8, 6, 7, 2}.
- We calculate the size of the array using the sizeof() operator and store it in the integer variable n. Then, print the array before sorting using the cout command and the for loop.
- Next, we call the bubbleSort() function, with the arr array and its size n as arguments to perform the sorting.
- Finally, we print the sorted elements of the array to the console.
Time Complexity: The time complexity of Bubble Sort in average cases is O(n^2). In the worst case, also, Bubble sort has a time complexity of O(n^2). For the best case, the time complexity of the Bubble sort is O(n).
Space Complexity: The space complexity of Bubble Sort is O(1).
How To Sort Array In C++ Using Insertion Sort?
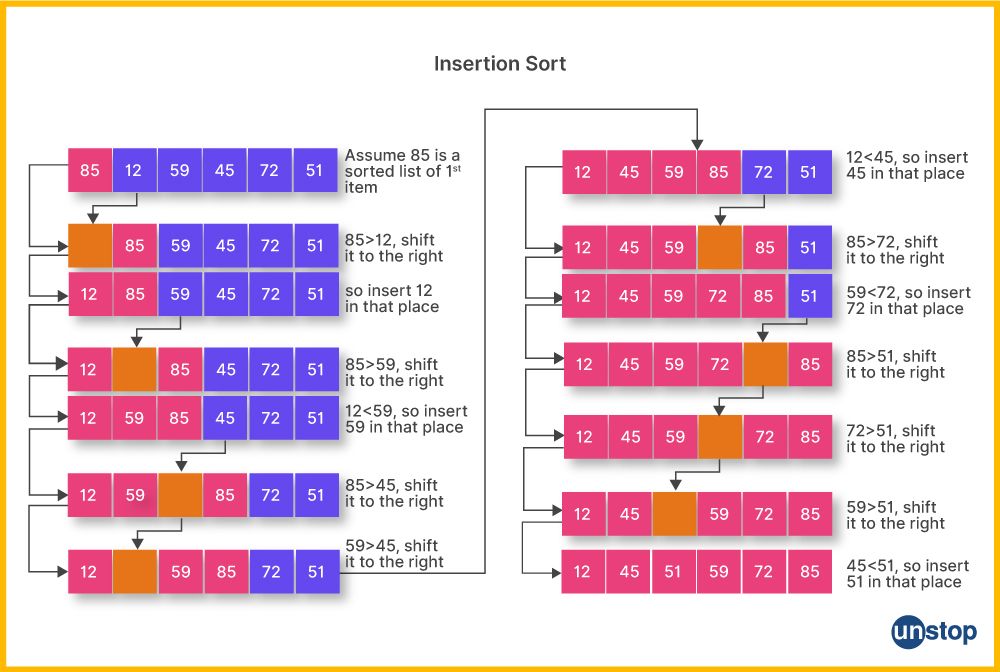
Insertion sort is a simple sorting algorithm that works by repeatedly taking an element from the unsorted portion of the array and inserting it into the correct position within the sorted portion. In other words, it builds the final sorted array one item at a time. Here's how insertion sort works:
- It starts by considering the first element of the array as the sorted portion.
- It then iterates through the remaining elements, inserting each element into its correct position within the already sorted portion.
- The algorithm continues this process until the entire array is sorted.
The algorithm iterates over the input listing, comparing each element to its adjoining values and transferring elements that are greater to the right.
This procedure is repeated till the entire array is sorted.
The Insertion Sort algorithm in C++ has the following syntax:
InsertionSort(p)
for j = 2 to length[p]
key = p[j]
i = j - 1
while i > 0 and p[i] > key
p[i + 1] = p[i]
i = i - 1
p[i + 1] = key
In this pseudocode,
- The character p refers to the array to be sorted using insertion sort.
- The for loop starts from the second element of the array and compares it with the preceding elements, moving them to the right till the correct position for the contemporary element (key) is determined.
- The key variable stores the element currently being sorted.
- The while loop shifts elements that are greater than the key to the right, making space for the key to be inserted into its correct position.
Note that the process in the pseudocode/syntax (of sorts) is repeated until the array at hand is sorted.
Code Example:
#include
using namespace std;
void insertionSort(int arr[], int n) {
int y, key, m;
// Loop through the array starting from the second element
for (y = 1; y < n; y++) {
key = arr[y];
m = y - 1;
// Shift elements that are greater than the key to one position ahead
while (m >= 0 && arr[m] > key) {
arr[m + 1] = arr[m];
m = m - 1;
}
// Insert the key at the correct position
arr[m + 1] = key;
}
}
int main() {
int arr[] = {9, 3, 5, 1, 8};
int n = sizeof(arr) / sizeof(arr[0]);
// Sort the array using insertion sort
insertionSort(arr, n);
// Print the sorted array
for (int y = 0; y < n; y++) {
cout << arr[y] << " ";
}
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgp1c2luZyBuYW1lc3BhY2Ugc3RkOwoKdm9pZCBpbnNlcnRpb25Tb3J0KGludCBhcnJbXSwgaW50IG4pIHsKaW50IHksIGtleSwgbTsKCi8vIExvb3AgdGhyb3VnaCB0aGUgYXJyYXkgc3RhcnRpbmcgZnJvbSB0aGUgc2Vjb25kIGVsZW1lbnQKZm9yICh5ID0gMTsgeSA8IG47IHkrKykgewprZXkgPSBhcnJbeV07Cm0gPSB5IC0gMTsKCi8vIFNoaWZ0IGVsZW1lbnRzIHRoYXQgYXJlIGdyZWF0ZXIgdGhhbiB0aGUga2V5IHRvIG9uZSBwb3NpdGlvbiBhaGVhZAp3aGlsZSAobSA+PSAwICYmIGFyclttXSA+IGtleSkgewphcnJbbSArIDFdID0gYXJyW21dOwptID0gbSAtIDE7Cn0KCi8vIEluc2VydCB0aGUga2V5IGF0IHRoZSBjb3JyZWN0IHBvc2l0aW9uCmFyclttICsgMV0gPSBrZXk7Cn0KfQoKaW50IG1haW4oKSB7CmludCBhcnJbXSA9IHs5LCAzLCA1LCAxLCA4fTsKaW50IG4gPSBzaXplb2YoYXJyKSAvIHNpemVvZihhcnJbMF0pOwoKLy8gU29ydCB0aGUgYXJyYXkgdXNpbmcgaW5zZXJ0aW9uIHNvcnQKaW5zZXJ0aW9uU29ydChhcnIsIG4pOwoKLy8gUHJpbnQgdGhlIHNvcnRlZCBhcnJheQpmb3IgKGludCB5ID0gMDsgeSA8IG47IHkrKykgewpjb3V0IDw8IGFyclt5XSA8PCAiICI7Cn0KCnJldHVybiAwOwp9
Output:
1 3 5 8 9
Explanation:
In the above C++ program,
- We define an insertionSort() function, which takes an integer array arr and its size n (int type) as parameters. Inside this function-
- We declare three integer variables, y, key, and m, where key will hold the current element we want to insert into the sorted portion of the array, while m helps in finding the correct position.
- Next, we enter a for loop, starting from the second element of the array (y = 1, since the first element arr[0] is considered as sorted) up to the last element (y = n-1).
- For each iteration of for loop, we store the element arr[y] in key variable and set m to y - 1, which represents the index of the previous element in the sorted portion.
- Then, we enter a while loop to compare and shift elements if needed. If any element in the sorted portion is greater than key, it is shifted one position to the right to make room for key. This process continues as long as m is greater than or equal to 0 and arr[m] is larger than the key.
- Outside the while loop, once the correct position is found, we insert key into arr[m + 1], which is the position just after the last shifted element.
- The for loop continues iterating until all elements of the array are sorted.
- Next, in the main() function, we declare an integer array arr and initialized with values {9, 3, 5, 1, 8}.
- After that, we calculate the size of the array, which is stored in the variable n using the sizeof() operator.
- We then call the insertionSort() function with the array arr and its size n as arguments to perform the sorting operation.
- Finally, we print the sorted array using for loop with the cout command.
Time Complexity: The time complexity of Insertion Sort for the best case scenario is O(n). In the worst case, the time complexity is O(n^2).
Space Complexity: The space complexity of Insertion Sort is O(1).
Check out this amazing course to become the best version of the C++ programmer you can be.
How To Sort An Array In C++ Using Selection Sort?
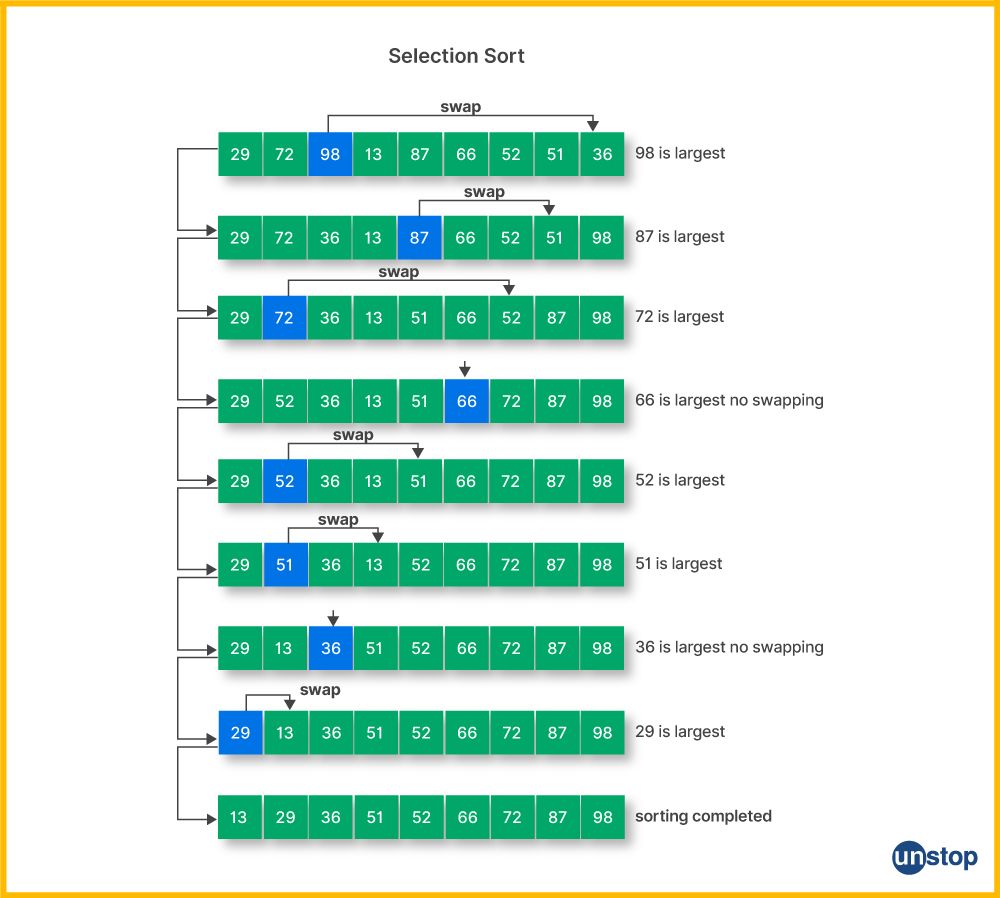
Selection sort is a straightforward sorting algorithm in C++ that works by repeatedly finding the minimum element from the unsorted portion of the array and swapping it with the first element of the unsorted subarray itself. Sounds confusing? Well, here is how selection sort works:
- The algorithm maintains two subarrays within the given array: a sorted subarray and an unsorted subarray.
- Note that initially, the unsorted subarray initially contains the full unsorted array, and the sorted subarray is empty (assumed to be at the beginning of the array).
- The algorithm finds the minimum/ least element of the unsorted subarray in every iteration, and swaps it with the element at the beginning of the unsorted subarray.
- This marks the beginning of the sorted portion of the array. This process continues until the unsorted subarray is empty and the entire array is sorted.
The Selection Sort algorithm in C++ has the following syntax:
void selectionSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
// to find the minimum element in the unsorted part of the array
int min_index = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[min_index]) {
min_index = j;}
}
//to swap the minimum element with the first element of the unsorted part
int temp = arr[i];
arr[i] = arr[min_index];
arr[min_index] = temp;
}
}
Here,
- The arr[] represents an integer array of size n, both of which are parameters for the selectionSort() function. It sorts the array in sort ascending order.
- The for keyword marks the beginning of for loop. We have a set of nested for loops, where the outer for loop traverses the array one current element at a time from index 0 to index n-2.
- Inner loop compares current element with the next element, to help decide if a swap must be made.
- The if statement inside the inner loop updates min_index if a smaller element is found.
- Once the minimum element is found, it is swapped with the first element of the unsorted part, effectively moving it to the beginning of the array.
Code Example:
#include
using namespace std;
void selectionSort(int arr[], int n) {
for (int h = 0; h < n - 1; h++) {
int min_index = h;
// Find the index of the minimum element in the unsorted part
for (int j = h + 1; j < n; j++) {
if (arr[j] < arr[min_index]) {
min_index = j;
}
}
// Swap the found minimum element with the first element of the unsorted part
int temp = arr[h];
arr[h] = arr[min_index];
arr[min_index] = temp;
}
}
int main() {
int arr[] = {5, 3, 8, 4, 2};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original array: ";
for (int h = 0; h < n; h++) {
cout << arr[h] << " ";
}
cout << endl;
// Sort the array using selection sort
selectionSort(arr, n);
cout << "Sorted array: ";
for (int h = 0; h < n; h++) {
cout << arr[h] << " ";
}
cout << endl;
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgoKdXNpbmcgbmFtZXNwYWNlIHN0ZDsKCnZvaWQgc2VsZWN0aW9uU29ydChpbnQgYXJyW10sIGludCBuKSB7CmZvciAoaW50IGggPSAwOyBoIDwgbiAtIDE7IGgrKykgewppbnQgbWluX2luZGV4ID0gaDsKCi8vIEZpbmQgdGhlIGluZGV4IG9mIHRoZSBtaW5pbXVtIGVsZW1lbnQgaW4gdGhlIHVuc29ydGVkIHBhcnQKZm9yIChpbnQgaiA9IGggKyAxOyBqIDwgbjsgaisrKSB7CmlmIChhcnJbal0gPCBhcnJbbWluX2luZGV4XSkgewptaW5faW5kZXggPSBqOwp9Cn0KCi8vIFN3YXAgdGhlIGZvdW5kIG1pbmltdW0gZWxlbWVudCB3aXRoIHRoZSBmaXJzdCBlbGVtZW50IG9mIHRoZSB1bnNvcnRlZCBwYXJ0CmludCB0ZW1wID0gYXJyW2hdOwphcnJbaF0gPSBhcnJbbWluX2luZGV4XTsKYXJyW21pbl9pbmRleF0gPSB0ZW1wOwp9Cn0KCmludCBtYWluKCkgewppbnQgYXJyW10gPSB7NSwgMywgOCwgNCwgMn07CmludCBuID0gc2l6ZW9mKGFycikgLyBzaXplb2YoYXJyWzBdKTsKCmNvdXQgPDwgIk9yaWdpbmFsIGFycmF5OiAiOwpmb3IgKGludCBoID0gMDsgaCA8IG47IGgrKykgewpjb3V0IDw8IGFycltoXSA8PCAiICI7Cn0KY291dCA8PCBlbmRsOwoKLy8gU29ydCB0aGUgYXJyYXkgdXNpbmcgc2VsZWN0aW9uIHNvcnQKc2VsZWN0aW9uU29ydChhcnIsIG4pOwoKY291dCA8PCAiU29ydGVkIGFycmF5OiAiOwpmb3IgKGludCBoID0gMDsgaCA8IG47IGgrKykgewpjb3V0IDw8IGFycltoXSA8PCAiICI7Cn0KY291dCA8PCBlbmRsOwoKcmV0dXJuIDA7Cn0=
Output:
Original array: 5 3 8 4 2
Sorted array: 2 3 4 5 8
Explanation:
In the sample C++ code, we show how to sort an array of numbers in ascending order using the selection sort method.
- To begin with, we define a selectionSort() function to perform the selection sort algorithm. It takes two parameters, i.e., an integer array arr, and the size of the array, i.e., variable n.
- Inside the selectionSort() function, we have a set of nested for loops:
- The outer for loop iterates from index 0 to n - 1. In each iteration, it first selects the next position in the sorted portion of the array, and places the minimum element from the unsorted portion in this place.
- Here, we declare and initialize an integer variable min_index to the value of h. This represents the index of the current minimum element, which is initially assumed to be the first element in the unsorted part of the array.
- Then, we use an inner for loop to iterate from h + 1 to n. In every iteration, it searches the unsorted part of the array for the smallest element by comparing each element to the current minimum (arr[min_index]) and updates min_index whenever a smaller element is found.
- Next, we have an if-statement inside the inner loop, which checks if an element is smaller than the current minimum (arr[j] < arr[min_index]). If this condition holds true, then min_index is modified to hold the value of j, thus ensuring that min_index always refers to the index of the smallest element of the unsorted section.
-
After finding the minimum element in the unsorted part, we swap this element with the first element of the unsorted portion. To do this, we temporarily store the value at index h in a variable temp, then assign the value at min_index to arr[h], and finally set arr[min_index] to temp.
- Then, in the main() function, we declare an integer array arr and initialized with unsorted values {5, 3, 8, 4, 2}. After that, we calculate the size of the array using the sizeof() operator and store it in variable n.
- The code then proceeds to print the elements of the array before sorting, using the cout command and a for loop.
- Next, we call the selectionSort() function with the arr array and its size n as arguments to perform the sorting.
- Finally, we use a for loop with a cout command to print the sorted array.
Time Complexity: The best-case time complexity is O(n^2), and the worst-case time complexity is O(n^2).
Space Complexity: The space complexity of the Selection Sort is O(1).
Level up your coding skills with the 100-Day Coding Sprint at Unstop and earn your bragging rights today!
How To Sort An Array In C++ Using Quicksort?
Quicksort is a widely used sorting algorithm in C++ that follows the "divide-and-conquer" approach. Meaning, it selects a pivot element, divides the array into sub-arrays (one with elements smaller than the pivot and other with remaining), and recursively sorts (conquers) the sub-arrays. Here’s how quicksort works:
- Under this technique, a pivot element is chosen from the array. This pivot can be any element (commonly the first, last, or middle element, or even a randomly selected one).
- The array undergoes a partitioning step in which it is divided into sub-arrays based mostly on a delegated pivot element.
- Elements smaller than the pivot are grouped into the left sub-array, whilst elements equal to or more than the pivot are positioned inside the right sub-array.
- This partitioning is completed by using the use of two pointers placed at the ends of the sub-array, gradually shifting towards each other till they converge.
- The left and right sub-arrays are then recursively sorted using the same manner using the quicksort() function.
- Finally, while all the sub-arrays have been sorted, the array is organized in ascending order.
The Quick Sort algorithm in C++ has the following syntax:
void quickSort(int arr[], int left, int right) {
//if sub-array has less than 2 elements
if (left >= right) {
return;
}
int pivot = arr[(left + right) / 2];
int i = left, j = right; // partition sub-array
while (i <= j) {
while (arr[i] < pivot) {
i++;}
while (arr[j] > pivot) {
j--;}
if (i <= j) {
std::swap(arr[i], arr[j]);
i++;
j--;}
}
quickSort(arr, left, j); // recursively sort left and right sub-arrays
quickSort(arr, i, right);
}
Here,
- Integer array arr[] refers to the array to be sorted, with integer variables left and right representing the subarray's leftmost and rightmost indexes, respectively. The quickSort() function accepts them as parameters.
- Integer variable pivot refers to the pivot element, i.e., the sub-array's middle element.
- We use while loops and if-statements to check conditions and carry out the sorting.
By swapping elements that might be on the incorrect side of the pivot, the sub-array is ultimately divided into two sub-arrays. The two ensuing sub-arrays are then sorted recursively using the QuickSort function.
Code Example:
#include
void quickSort(int arr[], int left, int right) {
if (left >= right) {
return;
}
int pivot = arr[left]; // Choose the pivot as the leftmost element
int i = left + 1; // Start from the element next to the pivot
int j = right;
while (i <= j) {
// Find an element greater than the pivot
while (i <= j && arr[i] <= pivot) {
i++;
}
// Find an element smaller than the pivot
while (i <= j && arr[j] > pivot) {
j--;
}
if (i < j) {
std::swap(arr[i], arr[j]);
}
}
// Move the pivot to its correct position
std::swap(arr[left], arr[j]);
// Recursively sort the sub-arrays
quickSort(arr, left, j - 1);
quickSort(arr, j + 1, right);
}
int main() {
int arr[] = {9, 4, 2, 7, 1, 5, 3};
int size = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, size - 1);
std::cout << "Sorted array: ";
for (int i = 0; i < size; i++) {
std::cout << arr[i] << " ";
}
std::cout << std::endl;
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgoKdm9pZCBxdWlja1NvcnQoaW50IGFycltdLCBpbnQgbGVmdCwgaW50IHJpZ2h0KSB7CmlmIChsZWZ0ID49IHJpZ2h0KSB7CnJldHVybjsKfQoKaW50IHBpdm90ID0gYXJyW2xlZnRdOyAvLyBDaG9vc2UgdGhlIHBpdm90IGFzIHRoZSBsZWZ0bW9zdCBlbGVtZW50CmludCBpID0gbGVmdCArIDE7IC8vIFN0YXJ0IGZyb20gdGhlIGVsZW1lbnQgbmV4dCB0byB0aGUgcGl2b3QKaW50IGogPSByaWdodDsKCndoaWxlIChpIDw9IGopIHsKLy8gRmluZCBhbiBlbGVtZW50IGdyZWF0ZXIgdGhhbiB0aGUgcGl2b3QKd2hpbGUgKGkgPD0gaiAmJiBhcnJbaV0gPD0gcGl2b3QpIHsKaSsrOwp9Ci8vIEZpbmQgYW4gZWxlbWVudCBzbWFsbGVyIHRoYW4gdGhlIHBpdm90CndoaWxlIChpIDw9IGogJiYgYXJyW2pdID4gcGl2b3QpIHsKai0tOwp9CmlmIChpIDwgaikgewpzdGQ6OnN3YXAoYXJyW2ldLCBhcnJbal0pOwp9Cn0KCi8vIE1vdmUgdGhlIHBpdm90IHRvIGl0cyBjb3JyZWN0IHBvc2l0aW9uCnN0ZDo6c3dhcChhcnJbbGVmdF0sIGFycltqXSk7CgovLyBSZWN1cnNpdmVseSBzb3J0IHRoZSBzdWItYXJyYXlzCnF1aWNrU29ydChhcnIsIGxlZnQsIGogLSAxKTsKcXVpY2tTb3J0KGFyciwgaiArIDEsIHJpZ2h0KTsKfQoKaW50IG1haW4oKSB7CmludCBhcnJbXSA9IHs5LCA0LCAyLCA3LCAxLCA1LCAzfTsKaW50IHNpemUgPSBzaXplb2YoYXJyKSAvIHNpemVvZihhcnJbMF0pOwoKcXVpY2tTb3J0KGFyciwgMCwgc2l6ZSAtIDEpOwoKc3RkOjpjb3V0IDw8ICJTb3J0ZWQgYXJyYXk6ICI7CmZvciAoaW50IGkgPSAwOyBpIDwgc2l6ZTsgaSsrKSB7CnN0ZDo6Y291dCA8PCBhcnJbaV0gPDwgIiAiOwp9CnN0ZDo6Y291dCA8PCBzdGQ6OmVuZGw7CgpyZXR1cm4gMDsKfQ==
Output:
Sorted array: 1 2 3 4 5 7 9
Explanation:
In the sample C++ program above,
- We define the quickSort() function to implement the QuickSort algorithm. It takes three parameters, i.e., arr (an integer array), left (index of the leftmost element in the sub-array to be sorted), and right (index of the rightmost element in the sub-array to be sorted).
- Inside the quickSort() function-
- We use an if-statement to check the base case for the recursive call. If the left index is greater than or equal to the right index, it means the sub-array has only one element or no elements. In such cases, the function returns immediately as there's nothing to sort.
- If not, then the function chooses the leftmost element (arr[left]) as the pivot element, i.e., int pivot = arr[left].
- Next, we initialize two pointers: i starts at left + 1 (just after the pivot), and j starts at right (the last element of the sub-array). These pointers are used to scan the array from both ends.
- We then initiate three nested while loops. The outermost loop continues until i <= j holds true.
- The two inner loops search for two elements to swap, i.e., an element greater than the pivot on the left side (arr[i]) and an element smaller than or equal to the pivot on the right side (arr[j]).
- The while loop that increments i searches for the element greater than the pivot, and the while loop that decrements j searches for the element smaller than or equal to the pivot.
- Then, an if statement checks condition (i<j), which means the two elements to be swapped have been found. The elements at positions i and j are then swapped using std::swap.
- The while loop continues until i becomes greater than j, indicating that all necessary swaps have been performed.
- After the loop, the pivot element (arr[left]) is swapped with the element at position j. This places the pivot element in its correct sorted position.
- Later, we apply recursion by invoking quickSort() multiple times to sort the sub-arrays positioned on the left and right sides of the pivot element. The process repeats until all sub-arrays are sorted.
- Then, in the main() function, we declare an integer array arr and initialize with values {9, 4, 2, 7, 1, 5, 3}. After that, we calculate the size of the array using sizeof() operator and store it in variable n.
- Next, we call the quickSort() function with the arr array, left initialized to 0, and right initialized to size - 1, as arguments. In other words, the entire array is the range for the function, which it sorts in place.
- Finally, we print the elements of the array after sorting using the cout command and a for loop to demonstrate the sorted order.
Time Complexity: The best-case scenario has a time complexity of O(n log n), and the worst-case scenario time complexity is O(n^2).
Space Complexity: The space complexity of Quick Sort is O(log n).
How To Sort Array In C++ Using Merge Sort?
Merge sort is another sorting algorithm in C++ that also follows the "divide-and-conquer" approach. It divides the input array into two equal halves and continues the division until the subarrays have only one element each (considered sorted).
It then recursively sorts the subarrays individually to produce a single sorted array by merging the subarrays back together. The elements from the two subarrays are compared throughout the merging process, and then they are added to the original array in the proper order.
Code Example:
#include
using namespace std;
// Merge two sorted subarrays into a single sorted array
void merge(int arr[], int left[], int leftSize, int right[], int rightSize) {
int i = 0, j = 0, k = 0;
// Compare elements from left and right subarrays and merge them into the original array
while (i < leftSize && j < rightSize) {
if (left[i] <= right[j]) {
arr[k] = left[i];
i++;
} else {
arr[k] = right[j];
j++;
}
k++;
}
// Copy the remaining elements of left subarray
while (i < leftSize) {
arr[k] = left[i];
i++;
k++;
}
// Copy the remaining elements of right subarray
while (j < rightSize) {
arr[k] = right[j];
j++;
k++;
}
}
// Merge sort implementation
void mergeSort(int arr[], int size) {
if (size < 2)
return;
int mid = size / 2;
int left[mid];
int right[size - mid];
// Divide the array into two halves
for (int i = 0; i < mid; i++)
left[i] = arr[i];
for (int i = mid; i < size; i++)
right[i - mid] = arr[i];
// Recursively sort the two halves
mergeSort(left, mid);
mergeSort(right, size - mid);
// Merge the sorted halves
merge(arr, left, mid, right, size - mid);
}
// Utility function to print an array
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
int main() {
int arr[] = {12, 11, 13, 5, 6, 7};
int size = sizeof(arr) / sizeof(arr[0]);
cout << "Original array: ";
printArray(arr, size);
mergeSort(arr, size);
cout << "Sorted array: ";
printArray(arr, size);
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgp1c2luZyBuYW1lc3BhY2Ugc3RkOwoKLy8gTWVyZ2UgdHdvIHNvcnRlZCBzdWJhcnJheXMgaW50byBhIHNpbmdsZSBzb3J0ZWQgYXJyYXkKdm9pZCBtZXJnZShpbnQgYXJyW10sIGludCBsZWZ0W10sIGludCBsZWZ0U2l6ZSwgaW50IHJpZ2h0W10sIGludCByaWdodFNpemUpIHsKaW50IGkgPSAwLCBqID0gMCwgayA9IDA7CgovLyBDb21wYXJlIGVsZW1lbnRzIGZyb20gbGVmdCBhbmQgcmlnaHQgc3ViYXJyYXlzIGFuZCBtZXJnZSB0aGVtIGludG8gdGhlIG9yaWdpbmFsIGFycmF5CndoaWxlIChpIDwgbGVmdFNpemUgJiYgaiA8IHJpZ2h0U2l6ZSkgewppZiAobGVmdFtpXSA8PSByaWdodFtqXSkgewphcnJba10gPSBsZWZ0W2ldOwppKys7Cn0gZWxzZSB7CmFycltrXSA9IHJpZ2h0W2pdOwpqKys7Cn0KaysrOwp9CgovLyBDb3B5IHRoZSByZW1haW5pbmcgZWxlbWVudHMgb2YgbGVmdCBzdWJhcnJheQp3aGlsZSAoaSA8IGxlZnRTaXplKSB7CmFycltrXSA9IGxlZnRbaV07CmkrKzsKaysrOwp9CgovLyBDb3B5IHRoZSByZW1haW5pbmcgZWxlbWVudHMgb2YgcmlnaHQgc3ViYXJyYXkKd2hpbGUgKGogPCByaWdodFNpemUpIHsKYXJyW2tdID0gcmlnaHRbal07CmorKzsKaysrOwp9Cn0KCi8vIE1lcmdlIHNvcnQgaW1wbGVtZW50YXRpb24Kdm9pZCBtZXJnZVNvcnQoaW50IGFycltdLCBpbnQgc2l6ZSkgewppZiAoc2l6ZSA8IDIpCnJldHVybjsKCmludCBtaWQgPSBzaXplIC8gMjsKaW50IGxlZnRbbWlkXTsKaW50IHJpZ2h0W3NpemUgLSBtaWRdOwoKLy8gRGl2aWRlIHRoZSBhcnJheSBpbnRvIHR3byBoYWx2ZXMKZm9yIChpbnQgaSA9IDA7IGkgPCBtaWQ7IGkrKykKbGVmdFtpXSA9IGFycltpXTsKZm9yIChpbnQgaSA9IG1pZDsgaSA8IHNpemU7IGkrKykKcmlnaHRbaSAtIG1pZF0gPSBhcnJbaV07CgovLyBSZWN1cnNpdmVseSBzb3J0IHRoZSB0d28gaGFsdmVzCm1lcmdlU29ydChsZWZ0LCBtaWQpOwptZXJnZVNvcnQocmlnaHQsIHNpemUgLSBtaWQpOwoKLy8gTWVyZ2UgdGhlIHNvcnRlZCBoYWx2ZXMKbWVyZ2UoYXJyLCBsZWZ0LCBtaWQsIHJpZ2h0LCBzaXplIC0gbWlkKTsKfQoKLy8gVXRpbGl0eSBmdW5jdGlvbiB0byBwcmludCBhbiBhcnJheQp2b2lkIHByaW50QXJyYXkoaW50IGFycltdLCBpbnQgc2l6ZSkgewpmb3IgKGludCBpID0gMDsgaSA8IHNpemU7IGkrKykKY291dCA8PCBhcnJbaV0gPDwgIiAiOwpjb3V0IDw8IGVuZGw7Cn0KCmludCBtYWluKCkgewppbnQgYXJyW10gPSB7MTIsIDExLCAxMywgNSwgNiwgN307CmludCBzaXplID0gc2l6ZW9mKGFycikgLyBzaXplb2YoYXJyWzBdKTsKCmNvdXQgPDwgIk9yaWdpbmFsIGFycmF5OiAiOwpwcmludEFycmF5KGFyciwgc2l6ZSk7CgptZXJnZVNvcnQoYXJyLCBzaXplKTsKCmNvdXQgPDwgIlNvcnRlZCBhcnJheTogIjsKcHJpbnRBcnJheShhcnIsIHNpemUpOwoKcmV0dXJuIDA7Cn0=
Output:
Original array: 12 11 13 5 6 7
Sorted array: 5 6 7 11 12 13
Explanation:
In the above C++ program,
- We define a merge() function to merge two sorted subarrays into a single sorted array. It takes five parameters, i.e., the original array arr[], two sorted subarrays left[] and right[], and their respective sizes leftSize and rightSize.
- Inside the function-
- We declare three integer variables, i, j, and k, to track the current index in the left, right, and original arrays, respectively, as we merge the two subarrays.
-
Then, we use a while loop to compare elements from the left and right subarrays. Using an if-else statement, we check if the element in the left subarray is smaller or equal to the element in the right subarray.
-
If the condition is true, we place the current element arr[k] in the original array at i-th position (left[i]), and increment both i and k.
-
If the element from the right subarray is smaller, we place it in the original array, and increment j and k.
- Once one of the subarrays is fully traversed, we use two additional while loops to copy any remaining elements from the left or right subarray into the original array.
- Next, we define a mergeSort() function to implement the merge sort algorithm. It takes two parameters, i.e., the original array arr and its size size. Inside the mergeSort() function-
- We use an if statement to check the condition if the size of the array is less than 2. If it is, then the function returns immediately as there's nothing to sort.
- If the condition is false, we calculate the midpoint mid of the array and declare two new arrays, left (with the size mid) and right (with capacity of size-mid), to hold the left and right half of the original array, respectively.
- We then use two for loops to divide the original array into two halves by copying elements at index less than mid, in the left subarray and the remaining in the right subarray.
- Next, we sort the two subarray by recursively calling the mergeSort() function on them.
- Once both halves are sorted, we call the merge() function to merge the sorted subarrays back into the original array.
- Next, we define a printArray() function, which prints the elements of an array using a for loop and the cout command.
- In the main() function, we declare an integer array arr and initialize it with integer values {12, 11, 13, 5, 6, 7}. Then, we calculate the size of the array using the sizeof() operatorand store that in variable n.
- We call the mergeSort() function with the arr array and its size as arguments, to sort the entire array. Afte that, we print it to the console using the printArray() function.
Time Complexity: The best-case time complexity is O(n log n), and the worst-case time complexity is O(n log n).
Space Complexity: The space complexity of Merge Sort is O(n).
How To Sort Data in C++ With Custom Function?
Instead of using the built-in comparison operations provided by the C++, you can employ a user-defined function to sort data based on specific requirements. This involves grouping together data components based on a specific comparison criterion:
- Say you have a list of complex items, and you want to reserve them by means of a positive attribute or set of attributes that the computer language's integrated sorting mechanism does not support.
- In this case, you can create a custom function that accepts two objects as input and outputs -1, 0, or 1 depending on whether the desired attribute values of the two objects compare favorably.
- The language's sorting algorithm can then be used with this custom function as an argument to decide the order of the items in the resulting sorted list.
Code Example:
#include
#include
using namespace std;
// Define the custom sorting function
bool customSort(int a, int b) {
// Sort even numbers first
if (a % 2 == 0 && b % 2 == 1) {
return true;
}
// Sort odd numbers last
else if (a % 2 == 1 && b % 2 == 0) {
return false;
}
// For even or odd numbers, sort in ascending order
else {
return a < b;
}
}
int main() {
int arr[] = {4, 1, 5, 2, 3, 6};
int n = sizeof(arr) / sizeof(arr[0]);
// Sort the array using the custom sorting function
sort(arr, arr + n, customSort);
// Print the sorted array to the console
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgojaW5jbHVkZSA8YWxnb3JpdGhtPgp1c2luZyBuYW1lc3BhY2Ugc3RkOwoKLy8gRGVmaW5lIHRoZSBjdXN0b20gc29ydGluZyBmdW5jdGlvbgpib29sIGN1c3RvbVNvcnQoaW50IGEsIGludCBiKSB7Ci8vIFNvcnQgZXZlbiBudW1iZXJzIGZpcnN0CmlmIChhICUgMiA9PSAwICYmIGIgJSAyID09IDEpIHsKcmV0dXJuIHRydWU7Cn0KLy8gU29ydCBvZGQgbnVtYmVycyBsYXN0CmVsc2UgaWYgKGEgJSAyID09IDEgJiYgYiAlIDIgPT0gMCkgewpyZXR1cm4gZmFsc2U7Cn0KLy8gRm9yIGV2ZW4gb3Igb2RkIG51bWJlcnMsIHNvcnQgaW4gYXNjZW5kaW5nIG9yZGVyCmVsc2UgewpyZXR1cm4gYSA8IGI7Cn0KfQoKaW50IG1haW4oKSB7CmludCBhcnJbXSA9IHs0LCAxLCA1LCAyLCAzLCA2fTsKaW50IG4gPSBzaXplb2YoYXJyKSAvIHNpemVvZihhcnJbMF0pOwoKLy8gU29ydCB0aGUgYXJyYXkgdXNpbmcgdGhlIGN1c3RvbSBzb3J0aW5nIGZ1bmN0aW9uCnNvcnQoYXJyLCBhcnIgKyBuLCBjdXN0b21Tb3J0KTsKCi8vIFByaW50IHRoZSBzb3J0ZWQgYXJyYXkgdG8gdGhlIGNvbnNvbGUKZm9yIChpbnQgaSA9IDA7IGkgPCBuOyBpKyspIHsKY291dCA8PCBhcnJbaV0gPDwgIiAiOwp9CmNvdXQgPDwgZW5kbDsKCnJldHVybiAwOwp9
Output
2 4 6 1 3 5
Explanation:
In the example above,
- We first define a customSort() function for sorting integers, which takes two integers, a and b, as parameters and returns a boolean value.
- The logic we implement in the customSort() function is:
- If a is even and b is odd, the function returns true, meaning a should come before b.
- If a is odd and b is even, the function returns false, indicating that b should come before a.
- For any other case, i.e., if both a and b are either even or odd, the function returns a < b to sort them in ascending order.
- In the main() function, we initialize an integer array arr with values {4, 1, 5, 2, 3, 6} and calculate its size n using the sizeof() operator.
- We then call the sort() function from the C++ Standard Library to sort the array. It takes three arguments: arr (the start of the array), arr+n (the end of the array), and out custom comparison function (customSort()), which defines the sorting logic.
- After that, we use a for loop (iterates from 0 to n-1) with a cout command to print each element of sorted array followed by a sapce.
Partial Sort Function To Sort An Array In C++
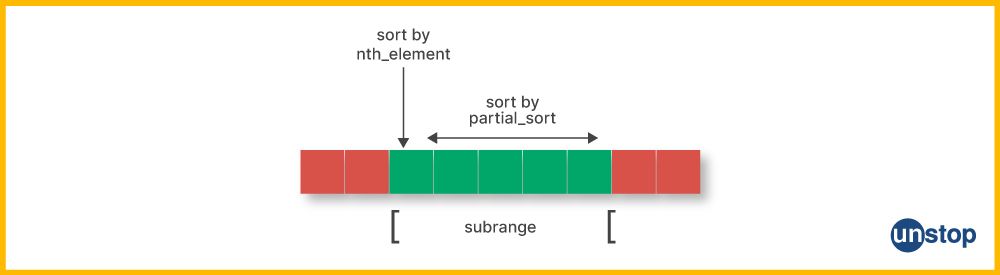
In C++, a partial sort is an algorithmic operation that sorts only a subset of a specified sequence or container rather than the complete collection. This allows you to bring the smallest (or largest, depending on the sorting order) elements to the front of the range while not necessarily sorting the entire range. The std::partial_sort function from the C++ Standard Library performs this task efficiently.
The syntax for Partial Sorting using std::partial_sort in C++ is as follows:
#include <algorithm>
std::partial_sort(first, middle, last);
Here:
- first: An iterator pointing to the beginning of the range to be partially sorted.
- middle: An iterator pointing to the element that marks the end of the partially sorted range. This is the position where the smallest (middle - first) elements will be placed in sorted order.
- last: An iterator pointing to the end of the range to be partially sorted.
Code Example:
#include
#include
int main() {
int numbers[] = {9, 5, 2, 8, 1, 7, 6, 3, 4};
int k = 4; // Number of elements to be partially sorted
// Partially sort the first 'k' elements in ascending order
std::partial_sort(numbers, numbers + k, numbers + 9);
// Print the partially sorted elements
for (int i = 0; i < k; i++) {
std::cout << numbers[i] << " ";
}
std::cout << std::endl;
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgojaW5jbHVkZSA8YWxnb3JpdGhtPgoKaW50IG1haW4oKSB7CmludCBudW1iZXJzW10gPSB7OSwgNSwgMiwgOCwgMSwgNywgNiwgMywgNH07CmludCBrID0gNDsgLy8gTnVtYmVyIG9mIGVsZW1lbnRzIHRvIGJlIHBhcnRpYWxseSBzb3J0ZWQKCi8vIFBhcnRpYWxseSBzb3J0IHRoZSBmaXJzdCAnaycgZWxlbWVudHMgaW4gYXNjZW5kaW5nIG9yZGVyCnN0ZDo6cGFydGlhbF9zb3J0KG51bWJlcnMsIG51bWJlcnMgKyBrLCBudW1iZXJzICsgOSk7CgovLyBQcmludCB0aGUgcGFydGlhbGx5IHNvcnRlZCBlbGVtZW50cwpmb3IgKGludCBpID0gMDsgaSA8IGs7IGkrKykgewpzdGQ6OmNvdXQgPDwgbnVtYmVyc1tpXSA8PCAiICI7Cn0Kc3RkOjpjb3V0IDw8IHN0ZDo6ZW5kbDsKCnJldHVybiAwOwp9
Output
1 2 3 4
Explanation
In this code,
- In the main() function, we declare and initialize an integer array called numbers, with the values {9, 5, 2, 8, 1, 7, 6, 3, 4}.
- We also declare an integer variable, k, and initialize it with the value of 4, indicating the number of elements to be partially sorted.
- Next, we call the std::partial_sort function to partially sort the first 'k' elements in ascending order. It takes three parameters-
- The initial parameter numbers, which is the beginning of the range to be partially sorted, representing the memory address of the first element in the array (numbers).
- The second parameter numbers + k, which is the end of the range to be sorted. This means we are sorting up to the first k elements.
- The third parameter numbers + 9, which specifies the end of the entire array. The function will use this to understand the bounds of the full array but only partially sort the specified range.
- The function will sort the first 'k' elements of the numbers array in ascending order, but the remaining elements beyond the 'k'-th position will not be sorted and may appear in any order.
- After performing the partial sort, we print the first k elements of the array. We use a for loop to iterate from 0 to k - 1, outputting each element followed by a space using the cout command.
Complexity Analysis
Given below is a comparison table, arranged in descending order from best to least based on average-case time complexity and space complexity:
| Sorting Algorithm | Time Complexity | Space Complexity |
| sort() Function | O(n log n) | O(log n) |
| qsort() Function | O(n log n) | O(log n) |
| Merge Sort Algorithm | O(n log n) | O(n) |
| Quicksort Algorithm | O(n log n) (Average Case) | O(log n) (Average Case) |
| Bubble Sort Algorithm | O(n^2) | O(1) |
| Insertion Sort Algorithm | O(n^2) | O(1) |
As we can notice from the above analysis, sort() and qsort() functions have the best average-case time complexity of O(n log n) with efficient space usage, followed by Merge Sort with similar time complexity but higher space requirements.
Quicksort also offers good average-case time complexity but has the potential for worst-case performance. Bubble Sort and Insertion Sort have poorer time complexity but minimal space needs.
Looking for mentors? Find the perfect mentor for select experienced coding & software experts here.
Conclusion
Sorting an array in C++ entails utilizing sorting algorithms like std::sort(), std::partial_sort(), bubble sort, insertion sort, selection sort, merge sort, or quicksort. Functions like std::sort() and std::partial_sort(), which are useful for quick sorting operations, are included in the C++ Standard Library.
When wondering how to sort an array in C++, all you have to do is choose the right algorithm according to your precise requirements. It is simpler to find and access individual elements when elements in an array are arranged in a particular order, thanks to sorting. Sorting arrays also makes the search operation easier. Overall, sorting arrays is a fundamental operation that offers a wide range of advantages in terms of data organization, search efficiency, data analysis, algorithmic efficiency, and result display.
Also read- 51 C++ Interview Questions For Freshers & Experienced (With Answers)
Frequently Asked Questions
Q. How to sort a 2D array in cpp using the sort function?
To sort a 2D array in C++, we need to use the std::sort function.
Code Example:
#include
#include
#include
bool compareRows(const std::vector& row1, const std::vector& row2) {
return row1[0] < row2[0]; // Sort based on the first column
}
int main() {
// Example 2D array
std::vector<std::vector> arr = {
{3, 2, 1},
{1, 4, 2},
{2, 3, 6}
};
// Sort the 2D array based on the first column
std::sort(arr.begin(), arr.end(), compareRows);
// Print the sorted array
for (const auto& row : arr) {
for (const auto& element : row) {
std::cout << element << " ";
}
std::cout << std::endl;
}
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgojaW5jbHVkZSA8YWxnb3JpdGhtPgojaW5jbHVkZSA8dmVjdG9yPgoKYm9vbCBjb21wYXJlUm93cyhjb25zdCBzdGQ6OnZlY3RvcjxpbnQ+JiByb3cxLCBjb25zdCBzdGQ6OnZlY3RvcjxpbnQ+JiByb3cyKSB7CnJldHVybiByb3cxWzBdIDwgcm93MlswXTsgLy8gU29ydCBiYXNlZCBvbiB0aGUgZmlyc3QgY29sdW1uCn0KCmludCBtYWluKCkgewovLyBFeGFtcGxlIDJEIGFycmF5CnN0ZDo6dmVjdG9yPHN0ZDo6dmVjdG9yPGludD4+IGFyciA9IHsKezMsIDIsIDF9LAp7MSwgNCwgMn0sCnsyLCAzLCA2fQp9OwoKLy8gU29ydCB0aGUgMkQgYXJyYXkgYmFzZWQgb24gdGhlIGZpcnN0IGNvbHVtbgpzdGQ6OnNvcnQoYXJyLmJlZ2luKCksIGFyci5lbmQoKSwgY29tcGFyZVJvd3MpOwoKLy8gUHJpbnQgdGhlIHNvcnRlZCBhcnJheQpmb3IgKGNvbnN0IGF1dG8mIHJvdyA6IGFycikgewpmb3IgKGNvbnN0IGF1dG8mIGVsZW1lbnQgOiByb3cpIHsKc3RkOjpjb3V0IDw8IGVsZW1lbnQgPDwgIiAiOwp9CnN0ZDo6Y291dCA8PCBzdGQ6OmVuZGw7Cn0KCnJldHVybiAwOwp9
Output:
1 4 2
2 3 6
3 2 1
Explanation:
In this example,
- The code first includes the iostream, algorithm, and vector header files. These header files provide the necessary functions and classes for the code to work.
- We then define a compareRows() function that takes two 2D arrays as input and returns true if the first array is less than the second array based on the first column. This function is used by the std::sort() algorithm to sort the 2D array.
- In the main() function, we declare a 2D array of integers and assign it some values.
- We then call the std::sort() function to sort the 2D array based on the first column. This function takes the beginning and end iterators of the array, as well as a comparison function, as input.
- The comparison function is used to determine the order of the elements in the array.
- Finally, we use a for loop to iterate through the sorted 2D array and the cout command to print each row to the console.
Q. How to sort an array in C++ using begin and end?
You can utilize the std::sort algorithm from the algorithm header in C++ to sort an array using the begin and end iterators. The std::sort() function takes two iterators as arguments to specify the range of elements to be sorted. The begin() and end() functions are used to obtain these iterators.
Code Example:
#include
#include
int main() {
int arr[] = {5, 2, 8, 1, 9};
int size = sizeof(arr) / sizeof(arr[0]); // Determine the size of the array
// Sort the array using begin and end
std::sort(std::begin(arr), std::end(arr));
// Print the sorted array
for (int i = 0; i < size; ++i) {
std::cout << arr[i] << " ";
}
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgojaW5jbHVkZSA8YWxnb3JpdGhtPgoKaW50IG1haW4oKSB7CmludCBhcnJbXSA9IHs1LCAyLCA4LCAxLCA5fTsKaW50IHNpemUgPSBzaXplb2YoYXJyKSAvIHNpemVvZihhcnJbMF0pOyAvLyBEZXRlcm1pbmUgdGhlIHNpemUgb2YgdGhlIGFycmF5CgovLyBTb3J0IHRoZSBhcnJheSB1c2luZyBiZWdpbiBhbmQgZW5kCnN0ZDo6c29ydChzdGQ6OmJlZ2luKGFyciksIHN0ZDo6ZW5kKGFycikpOwoKLy8gUHJpbnQgdGhlIHNvcnRlZCBhcnJheQpmb3IgKGludCBpID0gMDsgaSA8IHNpemU7ICsraSkgewpzdGQ6OmNvdXQgPDwgYXJyW2ldIDw8ICIgIjsKfQoKcmV0dXJuIDA7Cn0=
Output:
1 2 5 8 9
Explanation:
- The code first includes the <iostream> and <algorithm> header files. These header files provide the necessary functions and classes for the code to work.
- in the main() function, we declare an array of integers and assign it some values.
- We then use the std::sort() algorithm to sort the array using the begin() and end() iterators. The begin() iterator points to the beginning of the array, and the end() iterator points to the end of the array.
- Finally, using a for loop we iterate through the sorted array and the cout command to print each element to the console.
Q. How to sort two arrays in one array?
One way to sort two arrays into a single array is by first combining the two arrays and then sorting the merged array.
Code Example:
#include
#include
int main() {
int arr1[] = {5, 2, 8};
int arr2[] = {1, 9, 3};
int size1 = sizeof(arr1) / sizeof(arr1[0]);
int size2 = sizeof(arr2) / sizeof(arr2[0]);
int mergedSize = size1 + size2;
int merged[mergedSize];
// Merge the arrays
std::merge(arr1, arr1 + size1, arr2, arr2 + size2, merged);
// Sort the merged array
std::sort(merged, merged + mergedSize);
// Print the sorted merged array
for (int i = 0; i < mergedSize; ++i) {
std::cout << merged[i] << " ";
}
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgojaW5jbHVkZSA8YWxnb3JpdGhtPgoKaW50IG1haW4oKSB7CmludCBhcnIxW10gPSB7NSwgMiwgOH07CmludCBhcnIyW10gPSB7MSwgOSwgM307CgppbnQgc2l6ZTEgPSBzaXplb2YoYXJyMSkgLyBzaXplb2YoYXJyMVswXSk7CmludCBzaXplMiA9IHNpemVvZihhcnIyKSAvIHNpemVvZihhcnIyWzBdKTsKCmludCBtZXJnZWRTaXplID0gc2l6ZTEgKyBzaXplMjsKaW50IG1lcmdlZFttZXJnZWRTaXplXTsKCi8vIE1lcmdlIHRoZSBhcnJheXMKc3RkOjptZXJnZShhcnIxLCBhcnIxICsgc2l6ZTEsIGFycjIsIGFycjIgKyBzaXplMiwgbWVyZ2VkKTsKCi8vIFNvcnQgdGhlIG1lcmdlZCBhcnJheQpzdGQ6OnNvcnQobWVyZ2VkLCBtZXJnZWQgKyBtZXJnZWRTaXplKTsKCi8vIFByaW50IHRoZSBzb3J0ZWQgbWVyZ2VkIGFycmF5CmZvciAoaW50IGkgPSAwOyBpIDwgbWVyZ2VkU2l6ZTsgKytpKSB7CnN0ZDo6Y291dCA8PCBtZXJnZWRbaV0gPDwgIiAiOwp9CgpyZXR1cm4gMDsKfQ==
Output:
1 2 3 5 8 9
Explanation:
In this example,
- We declare and initialize two arrays, arr1, and arr2, in the main() function.
- Then, we calculate the size of both arrays and store them in two different variables, i.e., size1 and size2.
- Using the addition operator, we add the sizes of the two arrays and store them in a new variable, mergedSize. We then use this size to declare a new array called merged to store the merged array.
- Next, we use the std::merge() algorithm to merge the two arrays into the merged array.
- We then call the std::sort() function to sort the merged array.
- Finally, we use a for loop and the cout command to print the collection of elements of the sorted merged array to the console.
Q. How do you write a custom sort function in CPP?
To write a custom sort function in C++, you can use the std::sort() algorithm with a custom comparison function. The custom comparison function takes two elements as input and returns true if the first element is less than the second element and false otherwise. Let's look at an example of a custom sort function that sorts an array of integers in descending order.
Code Example:
#include
#include
bool compare(int a, int b) {
return a > b;
}
int main() {
int arr[] = {1, 5, 2, 8, 9};
// Sort the array in descending order
std::sort(std::begin(arr), std::end(arr), compare);
// Print the sorted array
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); ++i) {
std::cout << arr[i] << " ";
}
return 0;
}
I2luY2x1ZGUgPGlvc3RyZWFtPgojaW5jbHVkZSA8YWxnb3JpdGhtPgoKYm9vbCBjb21wYXJlKGludCBhLCBpbnQgYikgewpyZXR1cm4gYSA+IGI7Cn0KCmludCBtYWluKCkgewppbnQgYXJyW10gPSB7MSwgNSwgMiwgOCwgOX07CgovLyBTb3J0IHRoZSBhcnJheSBpbiBkZXNjZW5kaW5nIG9yZGVyCnN0ZDo6c29ydChzdGQ6OmJlZ2luKGFyciksIHN0ZDo6ZW5kKGFyciksIGNvbXBhcmUpOwoKLy8gUHJpbnQgdGhlIHNvcnRlZCBhcnJheQpmb3IgKGludCBpID0gMDsgaSA8IHNpemVvZihhcnIpIC8gc2l6ZW9mKGFyclswXSk7ICsraSkgewpzdGQ6OmNvdXQgPDwgYXJyW2ldIDw8ICIgIjsKfQoKcmV0dXJuIDA7Cn0=
Output:
9 8 5 2 1
Explanation:
- This code first defines a custom comparison function called compare(). It takes two integers as input and returns true if the first integer is greater than the second integer and false otherwise.
- In the main() function, we declare an array of integers called arr and initialize it with the values 1, 5, 2, 8, and 9.
- We then sort this array in descending order using the std::sort() algorithm. In the sort function, the std::begin() iterator points to the beginning of the array, and the std::end() iterator points to the end of the array.
- The std::sort() algorithm will sort the array elements in descending order using the compare() function.
- Finally, we print the sorted output array using a for loop and the cout command.
This compiles our discussion on how to sort an array in C++. You might also be interested in reading the following:
- References In C++ | Declare, Types, Properties & More (+Examples)
- Virtual Function In C++ | A Comprehensive Guide For All (+Examples)
- Array Of Objects In C++ | A Complete Guide To Creation (Using Examples)
- Inline Function In C++ | Declare, Working, Examples & More!
- C++ Type Conversion & Type Casting Demystified (With Examples)
An economics graduate with a passion for storytelling, I thrive on crafting content that blends creativity with technical insight. At Unstop, I create in-depth, SEO-driven content that simplifies complex tech topics and covers a wide array of subjects, all designed to inform, engage, and inspire our readers. My goal is to empower others to truly #BeUnstoppable through content that resonates. When I’m not writing, you’ll find me immersed in art, food, or lost in a good book—constantly drawing inspiration from the world around me.
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter












Comments
Add comment