Sort() Function In C++ & Algorithms Explained (+Code Examples)

0 min read

Sorting algorithms play a crucial role in thе world of computеr sciеncе, bringing ordеr to thе chaotic rеalm of data. It is a tool used in computеr programming to arrangе a collеction of itеms in a specific ordеr, such as ascеnding or dеscеnding. It is an essential coding skill because sorting data makes it easier to sеarch, analyzе, and prеsеnt. In this article, we will discuss the inbuilt sort() function in C++, explore its usage and underlying algorithms, and discuss best practices.

The concept of sorting has been around since the еarly days of computing, and various sorting algorithms like Bubblе Sort, Quick Sort, and Merge Sort were developed to efficiently organize data. Today, the sort function is a standard feature in programming languages, providing a convenient way to sort data without implеmеnting the sorting algorithm from scratch. So let's get started. 

What Is Sort() Function In C++?

The sort() function in C++ language is a built-in function that is used to sort any form of data structure in a desired order. It is defined in the <algorithm> header file. The syntax to use the inbuilt sort function in C++ is given below with components. 

Default Syntax For Sort() Function In C++:

template <typename RandomAccessIterator>
void sort(RandomAccessIterator first, RandomAccessIterator last);

Here,

• template <typename RandomAccessIterator> is the template declaration. Templates in C++ allow us to write code that can work with multiple data types without rewriting the code for each type.
• RandomAccessIterator is the parameter representing an iterator type that provides random access to elements, such as pointers and iterator types for arrays, vectors, and other containers.
• void sort(RandomAccessIterator first, RandomAccessIterator last) is the function signature for the std::sort function template.
• Void refers to the data type of the return value of the sort() function in C++
• RandomAccessIterator first represents an iterator pointing to the first element of the range you want to sort.
• RandomAccessIterator last represents an iterator pointing to the one-past-the-last element of the range we want to sort.

This syntax is the default form of the sort() function in C++. It sorts the elements in the range specified by the iterators first and last in ascending order using the default comparison operator (<).

Custom Syntax For Sort() Function In C++

bool comp(const data_type &a, const data_type &b) {
// function checks the desired relation between a and b and returns true if, according to the given relation, a should come before b in the sorted array
}

template <typename RandomAccessIterator, typename Compare>
void sort(RandomAccessIterator first, RandomAccessIterator last, Compare comp);

Here,

• bool comp(const data_type &a, const data_type &b) is a user-defined comparison function named comp. It takes two constant references to data_type objects as parameters, usually representing elements that need to be compared. The function returns true if a should come before b in the sorted array according to the defined relation.
• template <typename RandomAccessIterator, typename Compare> indicates the start of a function template declaration. 
• RandomAccessIterator is a type placeholder that represents an iterator type that supports random access (like pointers or vector iterators).
• Compare is another type of placeholder that represents a callable type (like a function pointer or a callable object) used for comparison.
• The sort() function syntax is similar to the one above. The only addition is a third parameter, Compare comp, which is an instance of the user-defined comparison function. This function will be used to determine the desired order of elements during the sorting process.

This syntax allows for custom sorting criteria. It takes the same range of elements to sort, specified by the iterators first and last. Additionally, it accepts a custom comparison function comp as its third argument. The return type of the comp function is boolean, and it performs the necessary checks while comparing two elements to decide their order in the sorted data structure.

Parameters Of The Sort() Function In C++

Based on the syntax classification made above, the following is the explanation of parameters used in the sort() function in C++:

1. First: It is an iterator, specifically a random access iterator, which can be used to access any element in a container directly without having to iterate through the elements in order. In this particular case, the iterator named as first points to the first element of the range to be sorted.
2. Last: Yes, you guessed it right! The last iterator used in the sort() function in C++ is also a random access iterator. But it points to the position just after the last element in the range to be sorted.
3. Comp: The comparator function passed as the third argument in the sort() function is a user-defined function that compares two elements of the container and returns true if the first element is less than the second element according to the desired criteria of sorting, which is defined inside the function body. The default value of the comparator function is std::less<T>, which compares two elements of type T and returns true if the first element is less than the second element.
4. Greater<data_type> (): It is a function object provided by the C++ Standard Library's <functional> header, specifically used to compare two elements of type data_type and determine if the first element is greater than the second element. It returns true if the first element is greater, which helps the sort() function in C++ rearrange the elements in descending order.

The Return Value Of Sort() Function In C++

The return type of the sort() function in C++ is void, which means it does not return any value that can be utilized by the caller. The purpose of the sort function is to rearrange the elements of the container in a desired order without providing any information or feedback about the sorting process.

Time Complexity Of Sort() Function In C++

The sorting algorithm used by std::sort() is typically an implementation of the introsort algorithm, which is a hybrid sorting algorithm combining quicksort, heapsort, and insertion sort (discussed in detail in the section ahead). Given below are the terms of time complexity for this function/ algorithm. 

• Worst Case: O(N log N)
  In the worst-case scenario, std::sort() exhibits a time complexity of O(N log N), where N is the number of elements to be sorted. If this happens, i.e., when the algorithm encounters a balanced split of the data and each level of recursion call, the data is split into nearly half the size.

• Average Case: O(N log N)

• Best Case: O(N log N)
  Unlike some other sorting algorithms, introsort (the implementation behind std::sort()) does not have a specific best-case behavior that results in significantly lower time complexity. So, the best-case time complexity is the same as that of the average case.

Space Complexity Of Sort() Function/ Algorithm In C++

The space complexity of std::sort() primarily involves the memory required for the recursive calls and the temporary storage for the algorithm's swaps and comparisons.

• Stack Space: The sorting algorithm uses a call stack for recursion. In the worst case, where the recursion depth is logarithmic with respect to the input size, the space complexity due to the call stack is O(log N).
• Auxiliary Space: The introsort algorithm requires some additional memory for temporary storage during the sorting process. This space complexity is generally considered to be O(N).

Note- Here, N is the number of elements being sorted.

Data Races In C++ Sort() Algorithm

A data race condition occurs in a program where two or more threads access the same memory location concurrently. At least one of them is a write operation, given there is the absence of any synchronization mechanism in place to ensure the correct order of these accesses.

When it comes to using the C++ std::sort() algorithm in a multithreaded context, potential data race conditions can arise if multiple threads are simultaneously modifying the elements of the container that are being sorted due to the involvement of multiple operations such as swapping, reordering, and comparison on the elements of the list.

We should ensure proper synchronization mechanisms are in place to avoid data races when using std::sort() in a multithreaded environment. Some of the strategies generally employed are:

• Mutexes or Locks: We can use mutexes or locks to protect access to the container while it's being sorted. This will prevent multiple threads from accessing and modifying the container's elements simultaneously.
• Thread-Local Containers: If each thread has its own set of elements to sort, we can avoid data races by ensuring that each thread operates on its own copy of the container.
• Parallel Algorithms: C++17 introduced parallel algorithms like std::sort()'s parallel version, std::sort(std::execution::par, ...), which automatically divides the work among multiple threads. These algorithms handle synchronization internally without the programmer’s intervention and can help mitigate data race issues.

Sort() Function In C++ From Standard Template Library

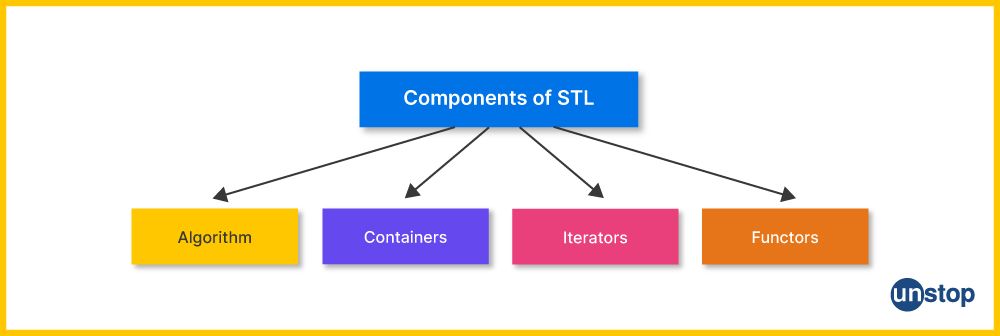
The Standard Template Library (STL) is a set of template classes that provides us the convenience of applying widely used components in C++ program development with ease. It is also the sort function in the C++ header file.

• STL has four main components, i.e., Containers, Algorithms, Iterators, and Functors (or function objects).
• Think of C++ STL as an application of the abstraction principle we studied in OOPS (Object Oriented Programming System), which basically aims at simplifying complex systems by breaking them down into manageable and understandable components.
• It involves hiding unnecessary implementation details and providing a simplified interface for users to interact with.

Similarly, STL abstracts away the low-level implementation details of various data structures and algorithms, allowing programmers to focus on the high-level logic of their programs.

Algorithms provided by the C++ STL are basically methods or functions that act on containers. However, here, we will focus on discussing some of the most widely used algorithms of C++ STL, the sort, and all the related algorithms.

Exceptions Of Sort() Function/ Algorithm In C++

While the sorting algorithms in C++ STL are generally robust, they can throw exceptions in certain scenarios. Some common exceptions that can be encountered while using C++ sorting algorithms include:

1. std::bad_alloc: This exception is thrown when there's insufficient memory available to perform the sorting operation. This is especially true if the sorting algorithms require extra memory space for temporary storage during the sorting process.
2. std::out_of_range: This exception can occur if the provided range for sorting is invalid. For example, if the iterators provided for the sorting range are out of bounds of the given list or incorrectly ordered, an out_of_range exception might be thrown.
3. Custom Exceptions: Depending on the specific sorting algorithm, their time and space complexity, the container type, and custom exceptions might be defined. For instance, some sorting algorithms like std::sort_heap and std::partial_sort throw a custom exception, std::invalid_argument, if the provided range or arguments are not valid.

The Stable Sort() Function In C++

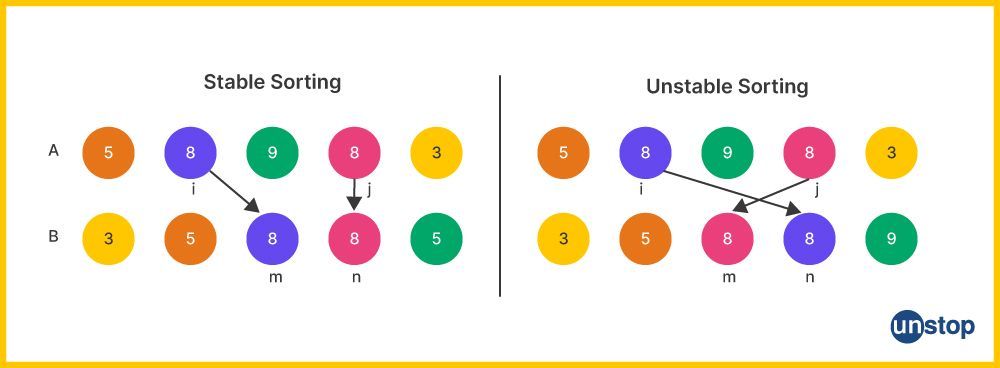
When sorting a collection of elements, the concept of a sort key becomes essential. The sort key is the basis for determining the order in which elements are arranged. In many sorting algorithms, if the sort key is the entire element itself, equal elements are considered indistinguishable. This means that elements with the same value may not necessarily maintain their relative order in the sorted collection.

However, there are scenarios where preserving the relative order of equal elements is crucial. This is where stable sorting algorithms come into play. A stable sort algorithm ensures that equal elements, when compared based on a sort key composed of one or more attributes of the element, retain their original order in the sorted result.

The syntax for stable sort is similar to the case of the normal sort() function in C++, given above. We just add the stable keyword right before sorting, as described below:

template <typename RandomAccessIterator>
void stable_sort(RandomAccessIterator first, RandomAccessIterator last);

Here,

• template <typename RandomAccessIterator> is the template parameter declaration. It signifies that the stable_sort function is a template function that works with a generic type.
• stable_sort is the name of the function you are using. It's the standard C++ algorithm that performs a stable sort on a given range of elements.

To use the stable_sort function, you need to provide the appropriate iterators that define the range of elements you want to sort, i.e., first and last. The function will then sort the elements in that range based on their values or use a custom comparison function if specified.

Code implementation of the stable sort() function in C++

I2luY2x1ZGUgPGJpdHMvc3RkYysrLmg+CnVzaW5nIG5hbWVzcGFjZSBzdGQ7CgppbnQgbWFpbigpIHsKdmVjdG9yPHBhaXI8aW50LCBzdHJpbmc+PiBkYXRhID0gewp7MywgIkFwcGxlIn0sCnsyLCAiT3JhbmdlIn0sCnsyLCAiQmFuYW5hIn0sCnsxLCAiR3JhcGUifSwKezEsICJNYW5nbyJ9Cn07Cgpzb3J0KGRhdGEuYmVnaW4oKSwgZGF0YS5lbmQoKSk7CmNvdXQgPDwgIkFmdGVyIHNvcnRpbmcgdXNpbmcgc29ydCAodW5zdGFibGUgc29ydCk6IiA8PCBlbmRsOwpmb3IgKGNvbnN0IGF1dG8mIHBhaXIgOiBkYXRhKSB7CmNvdXQgPDwgcGFpci5maXJzdCA8PCAiOiAiIDw8IHBhaXIuc2Vjb25kIDw8IGVuZGw7fQpjb3V0IDw8IGVuZGw7CmRhdGEgPSB7CnszLCAiQXBwbGUifSwKezIsICJPcmFuZ2UifSwKezIsICJCYW5hbmEifSwKezEsICJHcmFwZSJ9LAp7MSwgIk1hbmdvIn0KfTsKCnN0YWJsZV9zb3J0KGRhdGEuYmVnaW4oKSwgZGF0YS5lbmQoKSk7CmNvdXQgPDwgIkFmdGVyIHNvcnRpbmcgdXNpbmcgc3RhYmxlX3NvcnQgKHN0YWJsZSBzb3J0KToiIDw8IGVuZGw7CmZvciAoY29uc3QgYXV0byYgcGFpciA6IGRhdGEpIHsKY291dCA8PCBwYWlyLmZpcnN0IDw8ICI6ICIgPDwgcGFpci5zZWNvbmQgPDwgZW5kbDt9CnJldHVybiAwOwp9

This example compares the result of using the sort() function in C++ to that of using the stable sort function.

Output:

After sorting using sort (unstable sort):
1: Grape
1: Mango
2: Banana
2: Orange
3: Apple

After sorting using stable_sort (stable sort):
1: Grape
1: Mango
2: Orange
2: Banana
3: Apple

Explanation:

1. We begin the C++ program above by including the <bits/stdc++.h > header file, which includes most standard C++ headers.
2. Next, we start the main() function with a return type of int, which serves as the program's entry point.
3. We declare and initialize a vector of pairs named data inside the main function. Each pair consists of an integer and a string. This data represents items with associated numeric values.
4. We then use the sort() function in C++ from the Standard Library to sort the data vector. This sort is an unstable sort, meaning that items with equal values might not retain their original order.
5. We print the output of the console using the cout command and a for loop. 
6. Next, the data vector is reinitialized to its original values, and we call the stable_sort algorithm from the C++ Standard Library to sort the data vector again.
7. This result is printed to the console using cout and for loop.

The std::stable_sort in the C++ Standard Library typically uses a stable sorting algorithm such as mergesort to preserve the relative order of elements with equal sort keys.

Like the std::sort() function, the return type of the std::stable_sort() function is void. It modifies the container and doesn't return any information/feedback on the sorting process.

Time and Space complexity:

The time complexity of std::stable_sort depends on the available memory and the distance between the first and last elements in the range being sorted.

• If enough extra memory is available, then the time complexity of std::stable_sort is linearithmic, O(Nlog(N)), where N is the number of elements to be sorted.
• If limited extra memory is available, i.e., when the available memory is limited, the time complexity of std::stable_sort becomes poly log-linear, O(Nlog^2(N)).

Partial Sort() Function In C++

The partial sort function offers a specialized way to sort a portion of a collection or extract the smallest elements from a larger range. With partial_sort, we can efficiently obtain a sorted sub-range containing the smallest elements while leaving the remaining elements in an unspecified order.

This basic function is particularly useful when you only need a partial sort or want to prioritize performance by reducing the sorting effort to a specific portion of the collection.

There are two versions of the std::partial_sort() function in C++. The syntax is as follows:

template <class RandomAccessIterator>
void partial_sort(RandomAccessIterator first, RandomAccessIterator middle, RandomAccessIterator last);

And-

template <class RandomAccessIterator, class Compare>
void partial_sort(RandomAccessIterator first, RandomAccessIterator middle, RandomAccessIterator last, Compare comp);

Here,

• partial_sort is the name of the function. It's the identifier you use when you want to call this function.

• RandomAccessIterator first is the iterator pointing to the element at the beginning of the range we want to sort.
• RandomAccessIterator middle is the middle iterator pointing to the element that will be the middle of the sorted range. Elements before the middle element will be sorted in ascending order up to and including middle - 1, and elements after the middle will be unsorted.
• RandomAccessIterator last is the iterator pointing to the end of the range we want to sort partially.
• Compare comp is a function or functor that defines the comparison criterion for sorting the elements.

The elements present in the range from first to the middle are sorted according to the desired order, ensuring that the elements before the middle are sorted and the elements after the middle are left in an unspecified order.

Code implementation of the Partial Sort function in C++

I2luY2x1ZGUgPGJpdHMvc3RkYysrLmg+CnVzaW5nIG5hbWVzcGFjZSBzdGQ7CgppbnQgbWFpbigpIHsKdmVjdG9yPGludD4gbnVtYmVycyA9IHs0LCAyLCA1LCAxLCA3LCAzLCA4LCA2LCA5fTsKCi8vIFBhcnRpYWxseSBzb3J0IHRoZSBmaXJzdCA1IGVsZW1lbnRzIGluIGFzY2VuZGluZyBvcmRlcgpwYXJ0aWFsX3NvcnQobnVtYmVycy5iZWdpbigpLCBudW1iZXJzLmJlZ2luKCkgKyA1LCBudW1iZXJzLmVuZCgpKTsKCi8vIFByaW50IHRoZSBwYXJ0aWFsbHkgc29ydGVkIGVsZW1lbnRzCmNvdXQgPDwgIlBhcnRpYWxseSBzb3J0ZWQgZWxlbWVudHMgdXAgdG8gbWlkZGxlOiAiOwpmb3IgKGludCBpID0gMDsgaSA8IDU7IGkrKykgY291dCA8PCBudW1iZXJzW2ldIDw8ICIgIjsKY291dCA8PCBlbmRsOwoKLy8gT3JpZ2luYWwgZWxlbWVudHMgYmV5b25kIHRoZSBwYXJ0aWFsbHkgc29ydGVkIHJhbmdlIHJlbWFpbiB1bmNoYW5nZWQKY291dCA8PCAiT3JpZ2luYWwgZWxlbWVudHMgYWZ0ZXIgbWlkZGxlOiAiOwpmb3IgKGludCBpID0gNTsgaSA8IG51bWJlcnMuc2l6ZSgpOyBpKyspIHsKY291dCA8PCBudW1iZXJzW2ldIDw8ICIgIjt9CgpyZXR1cm4gMDsKfQ==

Output:

Partially sorted elements up to middle: 1 2 3 4 5
Original elements after middle: 7 8 6 9

Explanation:

The above code partially sorts the given vector up to index 4 and leaves the rest of the elements in an unspecified order.

1. Once again, we begin by including the bits/stdc++.h header file, which eliminates the need to include each library individually.
2. The std namespace contains all the standard C++ library functions, thus eliminating the need to write std:: before every function call.
3. Inside the int main() function, we declare and initialize a vector data structure named numbers, which is a dynamic array. This means it can grow and shrink as needed.
4. We then call the partial_sort() function to sort the first n (here, 5) elements in a range, where n is the second argument to the function. The remaining elements are not sorted.
5. Next, we use the cout object to print text to the console. Here, the endl object is used to print a newline character to the console.
6. The return statement returns a value from a function. In this case, the program returns 0 to indicate that it terminated successfully.

Time and Space complexity:

On average, the time complexity of partial_sort is less than linearithmic in the distance between the first and last iterators.

• It performs approximately N * log(M) comparisons of elements, where N represents the distance between first and last, and M represents the distance between first and middle.
• This sort of complexity indicates that the number of comparisons grows logarithmically with the size of the range being sorted.

The auxiliary space complexity of the std::partial_sort is considered to be constant O(1).

Thus far, we have discussed the sort() function in C++ in detail and have seen an implementation of the stable as well as partial sort. In the sections ahead, we will discuss how the sort function and other variations of the sorting algorithms can be used to sort data in various orders. 

Sorting In Ascending Order With Sort() Function In C++

The most common use case of the sort() function in C++ is to arrange elements of a container in ascending order. By default, the sort function arranges elements in ascending order when no custom comparison function is provided. The syntax for this is the same as the default syntax mentioned above in the article, which is:

template <typename RandomAccessIterator>
void sort(RandomAccessIterator first, RandomAccessIterator last);

Let’s take a look at an example of the implementation of the same.

Code Example:

I2luY2x1ZGUgPGJpdHMvc3RkYysrLmg+CnVzaW5nIG5hbWVzcGFjZSBzdGQ7CgppbnQgbWFpbigpIHsKdmVjdG9yPGludD4gbnVtYmVycyA9IHsxMCwgNCwgOCwgNSwgMTIsIDIsIDYsIDExLCAzLCA5LCA3LCAxfTsKY291dCA8PCAiT3JpZ2luYWwgQXJyYXk6ICI7CmZvciAoYXV0byBlOiBudW1iZXJzKSBjb3V0IDw8IGUgPDwgIiAiOwoKc29ydChudW1iZXJzLmJlZ2luKCksIG51bWJlcnMuZW5kKCkpOwpjb3V0IDw8ICJcblNvcnRlZCBBcnJheTogIjsKZm9yIChhdXRvIGU6IG51bWJlcnMpIGNvdXQgPDwgZSA8PCAiICI7CgpyZXR1cm4gMDsKfQ==

Output:

Original Array: 10 4 8 5 12 2 6 11 3 9 7 1
Sorted Array: 1 2 3 4 5 6 7 8 9 10 11 12

Code Explanation:

1. We define the int main() function in the example above, which is the entry point of the program.
2. In the main() function, we create a vector of integers, called numbers and initialize it with values- 10, 4, 8, 5, 12, 2, 6, 11, 3, 9, 7, 1.
3. Next, using the cout command and a for loop we print the original array to the console.
4. We then call the sort() fucntion in C++ to sort the array in descending order.
5. Finally, the program prints the sorted array to the console.

Sorting In Descending Order With Sort Function In C++

To sort elements in descending order, we use the greater<data_type>() function object provided by the C++ Standard Library's <functional> header. Given below is the syntax and an example for the same.

Sorting Syntax for Descending Order:

template <typename RandomAccessIterator, typename Compare>
void sort(RandomAccessIterator first, RandomAccessIterator last, greater<data_type>());

Here,

• void sort(RandomAccessIterator first, RandomAccessIterator last, greater<data_type>()) is the function call that sorts the range of elements defined by first and last using the greater<data_type> comparison object.
• The syntax is similar to that of the normal sort() function in C++, with the only difference being the third parameter, i.e., greater<data_type>().
• This is an instance of the greater template function object from the C++ Standard Library's <functional> header. It's used as the comparison function to sort the elements in descending order.

This syntax is a specific use case of sorting with a custom order of type such that the largest element is at the start and the smallest at the end. It utilizes the greater<data_type>() function object from the <functional> header. This functional object provides the comparison logic for sorting in reverse order.

Code Example:

I2luY2x1ZGUgPGJpdHMvc3RkYysrLmg+CnVzaW5nIG5hbWVzcGFjZSBzdGQ7CgppbnQgbWFpbigpIHsKdmVjdG9yPGludD4gbnVtYmVycyA9IHsxMCwgNCwgOCwgNSwgMTIsIDIsIDYsIDExLCAzLCA5LCA3LCAxfTsKY291dCA8PCAiT3JpZ2luYWwgQXJyYXk6ICI7CmZvciAoYXV0byBlOiBudW1iZXJzKSBjb3V0IDw8IGUgPDwgIiAiOwoKc29ydChudW1iZXJzLmJlZ2luKCksIG51bWJlcnMuZW5kKCksIGdyZWF0ZXI8aW50PigpKTsKY291dCA8PCAiXG5Tb3J0ZWQgQXJyYXk6ICI7CmZvciAoYXV0byBlOiBudW1iZXJzKSBjb3V0IDw8IGUgPDwgIiAiOwoKcmV0dXJuIDA7Cn0=

Output:

Original Array: 10 4 8 5 12 2 6 11 3 9 7 1
Sorted Array: 12 11 10 9 8 7 6 5 4 3 2 1

Code Explanation:

1. We begin the example by including the bits/stdc++.h header file and then define the main() function.
2. In the main() function, we declare a vector of integers called numbers and initialize it with some values. These values are printed to the console using cout and for loop. 
3. We then call the sort() function with greater<int> as a parameter to sort the numbers vector in descending order. 
4. The result is once again printed to the console before the program completes execution with return 0. 

Sorting In Desired Order With Custom Comparator Function & Sort Function In C++

The sort() function in C++ allows the use of a custom comparison function with a boolean return type to define a specific sorting order. By providing a comparison function, you can specify the criteria based on which the elements should be sorted. The comparison function should return true if the first element should come before the second element in the desired order.

Syntax for Custom Comparator function:

bool comp(const data_type &a, const data_type &b) {
// Define your comparison logic here
// Return true if 'a' should come before 'b', and false otherwise
// For example, to sort in descending order: return a > b;
}

Now, this comp function must be passed as a third argument to the sort function as described below:

std::sort(elements.begin(), elements.end(), comp);

Code Example:

I2luY2x1ZGUgPGJpdHMvc3RkYysrLmg+CnVzaW5nIG5hbWVzcGFjZSBzdGQ7Cgpib29sIGN1c3RvbV9jb21wYXJhdG9yKHBhaXI8aW50LCBpbnQ+IGEsIHBhaXI8aW50LCBpbnQ+IGIpIHsKcmV0dXJuIGEuc2Vjb25kIDwgYi5zZWNvbmQ7fQoKaW50IG1haW4oKSB7CnZlY3RvcjxwYWlyPGludCwgaW50Pj4gbnVtYmVycyA9IHt7MTAsIC0xfSwKezUsIDIwfSwKezEwMDAsIDJ9LAp7MTMsIDUwMH19Owpjb3V0IDw8ICJPcmlnaW5hbCBBcnJheTogXG4iOwpmb3IgKGF1dG8gZTogbnVtYmVycykgY291dCA8PCBlLmZpcnN0IDw8ICIgIiA8PCBlLnNlY29uZCA8PCBlbmRsOwoKc29ydChudW1iZXJzLmJlZ2luKCksIG51bWJlcnMuZW5kKCksIGN1c3RvbV9jb21wYXJhdG9yKTsKY291dCA8PCAiXG5Tb3J0ZWQgQXJyYXk6IFxuIjsKZm9yIChhdXRvIGU6IG51bWJlcnMpIGNvdXQgPDwgZS5maXJzdCA8PCAiICIgPDwgZS5zZWNvbmQgPDwgZW5kbDsKCnJldHVybiAwOwp9

Output:

Original Array:
10 -1
5 20
1000 2
13 500

Sorted Array:
10 -1
1000 2
5 20
13 500

Code Explanation:

1. in the example above, we define the custom_comparator function to implement a custom comparison for sorting pairs. It takes two pairs of integers, a and b, and compares their second elements.
2. The function returns true if the second element of a is less than the second element of b, indicating that a should come before b in the sorted order.
3. In the main() function, we declare a vector of integers in pairs, called numbers.
4. We initialize the vector with some values and print them to the console using the cout statement and a for loop.
5. Next, we call the sort() function to sort the elements in the vector if the initial condition is met. The sort function takes the beginning and ending iterators of the vector and the custom_comparator function as arguments.
6. This call to sort() function in C++ sorts the pairs based on the comparison defined in custom_comparator, which compares the second element of each pair.
7. After the sort function completes, the vector numbers with sorted pairs are printed to the console.

Note: The above custom comparator function sorts the elements of a vector, which happens to be a pair of integers, according to the second value in the pair.

Sorting Elements In Desired Order Using Lambda Expression & Sort Function In C++

The lambda expressions provide a concise way to define custom comparison functions inline. Instead of explicitly defining a separate comparison function, you can use lambda expressions directly as arguments to the sort function. This allows you to define the sorting criteria right at the point of invocation.

Syntax:

sort(array_name.begin(), array_name.end(), [](const data_type &a, const data_type &b) {
return (condition to keep a before b in sorted order);
})

Here,

• sort is the name of the sorting algorithm from the C++ Standard Library. It sorts the elements in the specified range according to the provided sorting criterion.
• array_name.begin() is an iterator pointing to the beginning of the range you want to sort.
• array_name.end() is an iterator pointing to the end of the range you want to sort.
• [](...) { ... } is the lambda function itself. A lambda function is an inline anonymous function that can be defined directly within the scope of a function call.
• (const data_type &a, const data_type &b) are the lambda function parameters. In this case, the lambda function takes two const references to elements of the array (or container) being sorted.
• return (condition to keep a before b in sorted order) is the return statement of the lambda function.

Code Example:

I2luY2x1ZGUgPGJpdHMvc3RkYysrLmg+CnVzaW5nIG5hbWVzcGFjZSBzdGQ7CgppbnQgbWFpbigpIHsKdmVjdG9yPHBhaXI8aW50LCBpbnQ+PiBudW1iZXJzID0ge3sxMCwgLTF9LAp7NSwgMjB9LAp7MTAwMCwgMn0sCnsxMywgNTAwfX07CmNvdXQgPDwgIk9yaWdpbmFsIEFycmF5OiBcbiI7CmZvciAoYXV0byBlOiBudW1iZXJzKSBjb3V0IDw8IGUuZmlyc3QgPDwgIiAiIDw8IGUuc2Vjb25kIDw8IGVuZGw7Cgpzb3J0KG51bWJlcnMuYmVnaW4oKSwgbnVtYmVycy5lbmQoKSwgW10ocGFpcjxpbnQsIGludD4gJmEsIHBhaXI8aW50LCBpbnQ+ICZiKSB7CnJldHVybiBhLnNlY29uZCA8IGIuc2Vjb25kOwp9KTsKY291dCA8PCAiXG5Tb3J0ZWQgQXJyYXk6IFxuIjsKZm9yIChhdXRvIGU6IG51bWJlcnMpIGNvdXQgPDwgZS5maXJzdCA8PCAiICIgPDwgZS5zZWNvbmQgPDwgZW5kbDsKCnJldHVybiAwOwp9

Here, the sorting criteria are similar to the example of a custom comparator function, just that we have defined the comparator at the call of the sort function itself.

Output:

Original Array:
10 -1
5 20
1000 2
13 500

Sorted Array:
10 -1
1000 2
5 20
13 500

Code Explanation:

1. In the main() function of the example above, we declare an integers vector called numbers, and initialize it with some values, which are printed using cout and a for loop. 
2. We then call the sort() function to sort the elements in the vector. It takes the beginning and ending iterators of the vector and a lambda expression as arguments.
3. The lambda expression [](pair<int, int>& a, pair<int, int>& b) { return a.second < b.second; } defines an anonymous function(function with no name) that acts as a custom comparator.
4. It compares two pairs of integers, a and b, based on their second elements and returns true if a should come before b in the sorted order (in this case, sorting in ascending order of the second element).
5. After the sort function completes, the vector numbers contain the sorted pairs, which are again printed to the console.

Types of Sorting Algorithms In C++

By now, you must know how to use the sort() function in C++ for sorting the elements of a structure/ container in ascending, descending, and even a custom order. 

Now, let’s dig deeper into the low-level procedure to sort a container and observe in detail the motion of elements inside the container based on various sorting algorithms. It's fascinating to witness how the arrangement of elements evolves as each algorithm applies its unique approach. Different sorting algorithms offer distinct trade-offs in terms of time and space performance, primarily influenced by the initial arrangement (or rather derangement) of the data. So let's get started!

Bubble Sort In C++

Bubble sort is a simple sorting algorithm that repeatedly steps through the array, compares adjacent elements, and swaps them if they are in the wrong order. This process is repeated until the entire array is sorted.

• The name bubble sort stems from the analogy between the movement of the smallest element in an array during one iteration of the algorithm and the upward movement of an air bubble in water.
• This comparison highlights the behavior of the sorting process, where the smallest (or largest) element 'bubbles' its way to its final position at the end (or beginning) of the array.

Let’s say the size of the array (which is to be sorted by bubble sort) is N. Then-

1. In the first pass, the total number of comparisons made will be N - 1.
2. In the second pass, as we are sure that one element is definitely at its desired position, which is the beginning of the array, the total number of comparisons made will be N - 2.
3. In the next pass, the number of comparisons will be N - 3, and so on.

Now, let's take a look at an example that showcases the implementation of the BubbleSort algorithm in C++.

Code Example:

I2luY2x1ZGUgPGJpdHMvc3RkYysrLmg+CnVzaW5nIG5hbWVzcGFjZSBzdGQ7Cgp2b2lkIGJ1YmJsZVNvcnQodmVjdG9yPGludD4mIGFycikgewppbnQgbiA9IGFyci5zaXplKCk7CmZvciAoaW50IGkgPSAwOyBpIDwgbiAtIDE7ICsraSkgewpmb3IgKGludCBqID0gMDsgaiA8IG4gLSBpIC0gMTsgKytqKSB7CmlmIChhcnJbal0gPiBhcnJbaiArIDFdKSB7CnN3YXAoYXJyW2pdLCBhcnJbaiArIDFdKTsKfQp9Cn0KfQoKaW50IG1haW4oKSB7CnZlY3RvcjxpbnQ+IGFyciA9IHs1LCA5LCA2LCA0LCA3LCAyLCAzLCAxLCA4fTsKaW50IE4gPSBhcnIuc2l6ZSgpOwpjb3V0IDw8ICJPcmlnaW5hbCBBcnJheTogIjsKZm9yIChhdXRvIGUgOiBhcnIpIHsKY291dCA8PCBlIDw8ICIgIjt9CgpidWJibGVTb3J0KGFycik7CmNvdXQgPDwgIlxuU29ydGVkIEFycmF5OiAiOwpmb3IgKGF1dG8gZSA6IGFycikgewpjb3V0IDw8IGUgPDwgIiAiO30KCnJldHVybiAwOwp9

Output:

Original Array: 5 9 6 4 7 2 3 1 8
Sorted Array: 1 2 3 4 5 6 7 8 9

Code explanation:

In the example above,

1. We define the bubbleSort() function to implement the Bubble Sort algorithm. In this function-
   • We have a reference to a vector arr as its parameter.
   • A variable n is declared and initialized with the size of the input array arr.
   • We also use a nested for loop with an if-statement. The outer loop iterates n-1 times while the inner loop compares adjacent elements and swaps them if they are in the wrong order.
   • If an adjacent pair of elements is out of order, the swap() function is called to swap their positions.
   • After the completion of each iteration of the outer loop, the largest element is guaranteed to be at the end of the array.
2. In the main() function, we declare and initialize an array called arr with some values. We also declare an integer variable N and initialize it with the size of the array.
3. Then, we print the array using the cout command and a for loop. 
4. Next, we call the bubbleSort() function to sort the array, and the sorted function is printed.

Time and Space complexity:

• Worst case: O(N2). This is when the array is sorted in descending order, and we need to sort it in ascending order.
• Average case: O(N2)
• Best case: O(N). This is when the array is already sorted.
• The auxiliary space required by the BubbleSort algorithm is O(1).

Insertion Sort In C++

Insertion sort is a straightforward sorting algorithm that builds the final sorted array one element at a time. It iterates through the array and inserts each element into its proper position within the sorted portion of the array, starting by assuming the first element to be sorted.

• The name 'insertion sort' reflects the process of inserting an element into its correct position.
• It shares a similarity with arranging a hand of cards in a card game, where the player repeatedly picks up a card and inserts it into the correct position in their hand.

Insertion sort basically consists of the following steps:

1. Assume the first element to be at the correct position that is sorted, and now pick the next element and store it as a key.
2. Compare the key with all the elements in the sorted part of the array. If the element in the sorted array is smaller than the current element, then move to the next element. Else, shift greater elements in the array towards the right.
3. Insert the key value and repeat until the entire array is sorted.

Code implementation of the InsertionSort algorithm in C++

I2luY2x1ZGUgPGJpdHMvc3RkYysrLmg+CnVzaW5nIG5hbWVzcGFjZSBzdGQ7Cgp2b2lkIGluc2VydGlvblNvcnQodmVjdG9yPGludD4mIGFycikgewppbnQgbiA9IGFyci5zaXplKCk7CmZvciAoaW50IGkgPSAxOyBpIDwgbjsgKytpKSB7CmludCBrZXkgPSBhcnJbaV07CmludCBqID0gaSAtIDE7CndoaWxlIChqID49IDAgJiYgYXJyW2pdID4ga2V5KSB7CmFycltqICsgMV0gPSBhcnJbal07CmotLTt9CmFycltqICsgMV0gPSBrZXk7fQp9CgppbnQgbWFpbigpIHsKdmVjdG9yPGludD4gYXJyID0gezYsIDUsIDMsIDEsIDgsIDcsIDIsIDR9OwppbnQgTiA9IGFyci5zaXplKCk7CmNvdXQgPDwgIk9yaWdpbmFsIEFycmF5OiAiOwpmb3IgKGF1dG8gZSA6IGFycikgewpjb3V0IDw8IGUgPDwgIiAiO30KCmluc2VydGlvblNvcnQoYXJyKTsKY291dCA8PCAiXG5Tb3J0ZWQgQXJyYXk6ICI7CmZvciAoYXV0byBlIDogYXJyKSB7CmNvdXQgPDwgZSA8PCAiICI7fQoKcmV0dXJuIDA7Cn0=

Output:

Original Array: 6 5 3 1 8 7 2 4
Sorted Array: 1 2 3 4 5 6 7 8

Code Explanation:

1. To begin with, we define the insertionSort() function to implement the insertion sort algorithm. It takes a reference to a vector arr as its parameter where n is the size of the vector.
2. Inside the function-
   • We have a for loop with a nested while loop inside. 
   • The outer loop iterates from the second element to the last element of the array. Inside this loop, the key variable stores the value of the current element being considered for insertion.
   • The inner loop checks if the current element is greater than the key. If so, it shifts the element one position to the right or continues moving backward until either the beginning of the array is reached, or an element that is smaller than or equal to the key is encountered.
   • Once the correct position for the key is found, it is inserted into the array at the appropriate index.
3. In the main() function, we declare an array called arr and initialize it with some values that are printed using the cout statement with a for loop.
4. We also declare a variable N and assign the size of the array to it. 
5. Next, we call the insertionSort() function to sort the array, after which the sorted array is printed to the console.

Time and Space complexity:

• Worst case: O(N2), i.e., when the array is sorted in descending order.
• Average case: O(N2)
• Best case: O(N), i.e., when the array is already sorted, the outer loop runs for n number of times, whereas the inner loop does not run at all.
• The auxiliary space required by the InsertionSort algorithm is O(1).

Selection Sort In C++

Selection sort is a straightforward sorting algorithm that divides the input array into two portions:

1. The sorted portion and
2. The unsorted portion.

It repeatedly selects the smallest (or largest) element from the unsorted portion and places it at the end (or beginning) of the sorted portion. The name 'selection sort' reflects the process of selecting the smallest (or largest) element and placing it in its correct position.

The selection sort process comprises the following three steps-

1. Identify the unsorted portion of the array. Initially, the entire array is considered unsorted.
2. Find the smallest (or largest) element in the unsorted portion. This involves iterating through the unsorted portion to compare each element with the current smallest (or largest) element.
3. Once the smallest (or largest) element is identified, swap it with the first element of the unsorted portion.

The last step increases the size of the sorted portion by one unit while simultaneously decreasing the size of the unsorted portion by one unit.

Code implementation of the SelectionSort algorithm in C++:

I2luY2x1ZGUgPGJpdHMvc3RkYysrLmg+CnVzaW5nIG5hbWVzcGFjZSBzdGQ7Cgp2b2lkIHNlbGVjdGlvblNvcnQodmVjdG9yPGludD4gJmFycikgewppbnQgbiA9IGFyci5zaXplKCk7CmZvciAoaW50IGkgPSAwOyBpIDwgbiAtIDE7ICsraSkgewppbnQgbWluSW5kZXggPSBpOwpmb3IgKGludCBqID0gaSArIDE7IGogPCBuOyArK2opIHsKaWYgKGFycltqXSA8IGFyclttaW5JbmRleF0pIHsKbWluSW5kZXggPSBqO30KfQpzd2FwKGFycltpXSwgYXJyW21pbkluZGV4XSk7Cn0KfQoKaW50IG1haW4oKSB7CnZlY3RvcjxpbnQ+IGFyciA9IHs4LCA1LCAyLCA2LCA5LCAzLCAxLCA0LCAwLCA3fTsKaW50IE4gPSBhcnIuc2l6ZSgpOwpjb3V0IDw8ICJPcmlnaW5hbCBBcnJheTogIjsKZm9yIChhdXRvIGU6IGFycikgewpjb3V0IDw8IGUgPDwgIiAiO30KCnNlbGVjdGlvblNvcnQoYXJyKTsKY291dCA8PCAiXG5Tb3J0ZWQgQXJyYXk6ICI7CmZvciAoYXV0byBlOiBhcnIpIHsKY291dCA8PCBlIDw8ICIgIjt9CgpyZXR1cm4gMDsKfQ==

Output:

Original Array: 8 5 2 6 9 3 1 4 0 7
Sorted Array: 0 1 2 3 4 5 6 7 8 9

Code Explanation:

1. We first define the selectionSort() function to implement the Selection Sort algorithm. It takes a reference to a vector, arr as its parameter, and n is the size of that vector.
2. Inside the function-
   • We have a nested for loop, where the inner loop has an if-statement. 
   • The outer loop iterates from the beginning of the array up to the second-to-last element, while the inner loop starts from the element after the current position and searches for the minimum element in the unsorted portion.
   • If an element smaller than the current minimum is found, its index is stored as the minIndex.
   • Once the inner loop finishes, the smallest element swaps with the element at the current position.
   • The outer loop continues until the entire array is sorted.
3. In the main() function, we declare a random array of integers called arr and print its values using cout and for loop.  
4. Next, we call the selectionSort() function to sort the array, after which the values are once again printed using the cout command. 

Time and Space complexity:

• Worst case: O(N2) (when the array is sorted in descending order)
• Average case: O(N2)
• Best case: O(N2) (When the array is already sorted)
• The auxiliary space required by the InsertionSort algorithm is O(1).

Advanced Sorting Algorithms In C++

Now that we've learned about basic sorting algorithms like Bubble Sort, Insertion Sort, and Selection Sort, it's time to venture into the world of more advanced techniques. These smart methods are specifically crafted to handle bigger sets of data and often outshine the simpler ones in terms of efficiency. In this section, we'll introduce a few advanced sorting algorithms, including Merge Sort, QuickSort, Counting Sort, Radix Sort, etc. Each of these methods uses unique strategies, some based on breaking the problem into smaller parts, while others take advantage of special characteristics of the data to achieve the best possible performance.

Merge Sort

Merge sort is a method of arranging items in an array from smallest to largest.

• It works by breaking the array into smaller pieces and sorting each piece separately.
• Then, it puts the sorted pieces back together to get the final sorted array.
• To do this, merge sort repeatedly divides the array in half until it can't be split any further (when there's only one item left in an array, it's already considered sorted).
• After that, it combines the sorted pieces one by one until the entire array is sorted.

Quick Sort

QuickSort is a sorting method that works by choosing a special element in the array called the 'pivot'. The goal is to put the pivot in its correct position in the sorted array.

• To achieve this, the algorithm divides the array into two parts, i.e., one with smaller elements than the pivot and another with greater elements.
• The pivot is placed between these two parts.
• To sort the entire array, QuickSort uses a process called partitioning.
• It repeatedly selects a pivot, arranges it in the correct position, and then recursively applies the same process to the smaller sub-array on each side of the pivot.
• This continues until the entire array is sorted.

Counting Sort

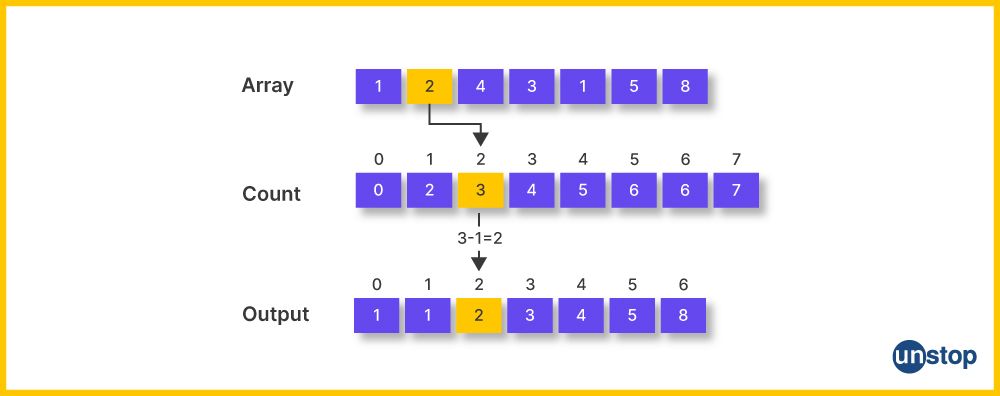
Counting sort is a method of sorting that is best suited when we have a range of specific numbers to sort.

• Instead of comparing individual elements like in some other sorting methods, counting sort counts how many times each number appears in the array.
• It then uses this counting information to figure out the correct order of the numbers in the final sorted array.
• It's like putting things in their places based on how many of each thing you have rather than comparing them one by one.
• This makes the counting sort() function in C++ very efficient for certain types of data sets.

Heap Sort

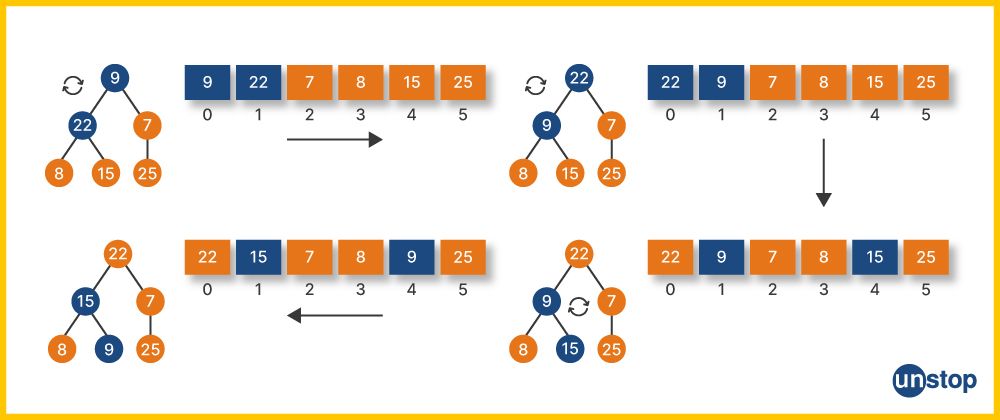
Heap sort is a way of sorting items in an array by using a special data structure called 'Binary Heap'. It works a bit like selection sort, where we find the smallest item and put it in the front. But in heap sort, we use a 'Max-heap', which means the largest item is at the root.

Here's how it works:

• First, we turn the array into a Max-heap. Think of it like arranging the items in a way that the biggest one is at the top and the rest follow in a specific order.
• Then, we repeatedly take the biggest item (at the top), move it to the end of the array, and make sure the remaining items are still in Max-heap order.
• We keep doing this until the whole array is sorted. It's like repeatedly picking the largest card from a deck and placing it at the back until all the cards are in ascending order.

Shell Sort

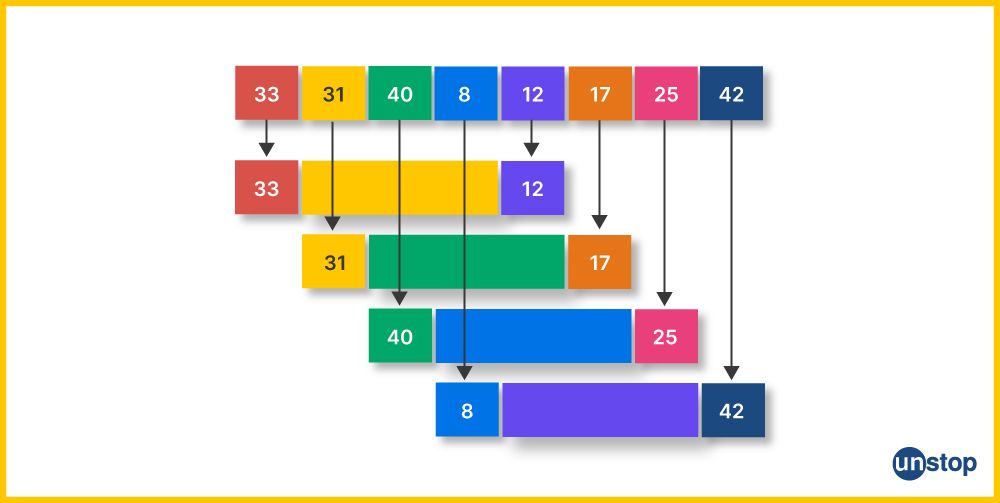
Shell sort is a modified version of Insertion Sort, a simple way of arranging items in an array. The problem with Insertion Sort is that when we need to move an item far ahead in the array, it requires many movements, which can be time-consuming. Shell sort aims to improve this by allowing the exchange of items that are far apart.

• Instead of sorting the array all at once, we first sort it partially for a relatively large 'h' value.
• Then, we gradually reduce the value of 'h' and sort the array again, repeating this process until 'h' becomes 1.
• When we say the array is 'h-sorted, it means that every h-th element and its sub-elements are sorted.
• This way, Shell sort tries to avoid excessive movement of items and makes the sorting process more efficient.

It's like taking smaller steps to sort the array and then fine-tuning it to get the final sorted order.

Radix Sort

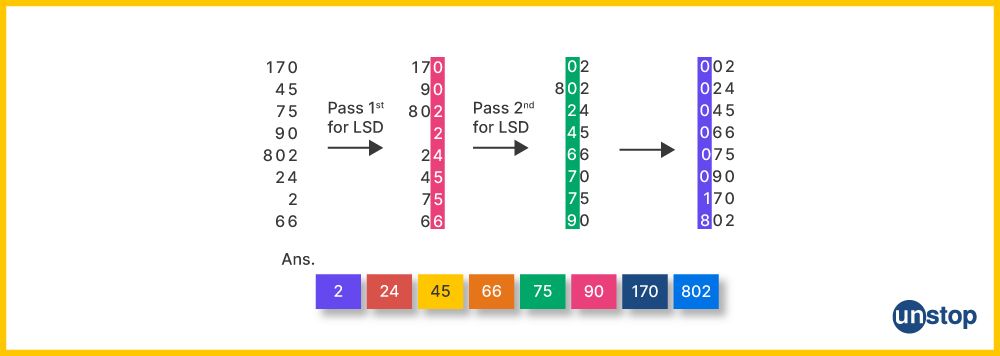
Radix Sort is a special way of sorting numbers or words with a fixed number of digits or letters. Instead of comparing the items directly, it sorts them digit by digit or letter by letter.

Imagine you have a bunch of numbers, and you want to sort them from smallest to largest using the RadixSort() function in C++.

• First, you start by looking at the rightmost digit of each number (the one's place) and put the numbers into separate buckets based on that digit.
• Then, you combine the numbers back together in the order they appear in the buckets.
• Next, you look at the next digit to the left (the tens place) and do the same process again.
• You keep doing this for each digit, moving from right to left until all the numbers are in the correct order.

Radix Sort is like organizing numbers by their place value, sorting them one place at a time until the whole array is sorted. It's a unique way of sorting that works well for numbers or words with the same length, and it can be done in different ways depending on which end you start from.

How Does the Sort() Function Algorithm Work In C++?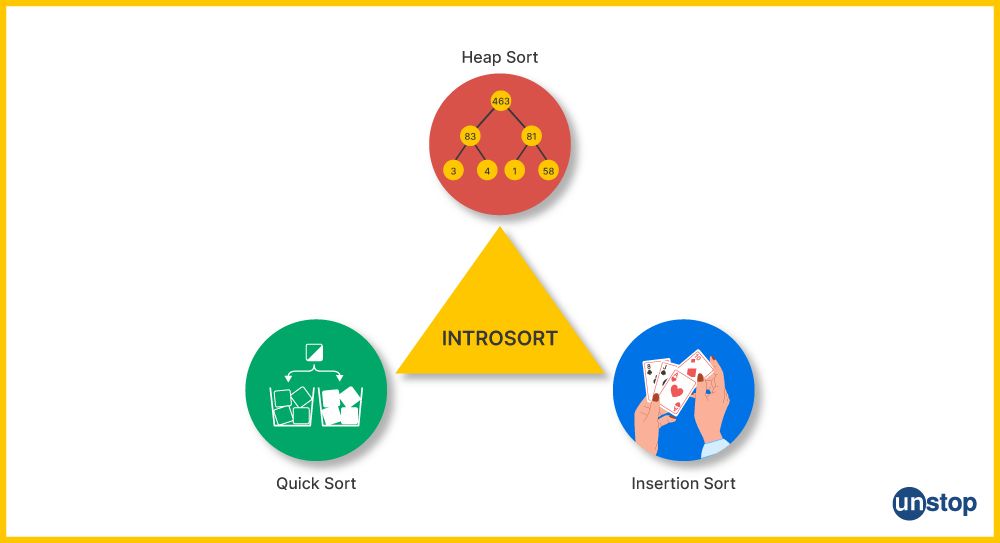

After exploring numerous sorting algorithms, you might be wondering which algorithm is actually used by the built-in sort() function in C++.

Well, the sort() function in C++ implements an algorithm called introsort. Introsort, also known as introspective sort, is a hybrid sorting algorithm that offers a balance between fast average performance and optimal worst-case performance.

• It starts by utilizing quicksort, a popular sorting algorithm known for its efficiency on average data sets.
• However, introsort dynamically adjusts its strategy to prevent potential performance issues.
• When the recursion depth reaches a certain level based on the logarithm of the number of elements being sorted, introsort switches to heapsort.
• Heapsort guarantees a worst-case runtime of O(n log n). Additionally, if the number of elements to be sorted is below a specific threshold, introsort transitions to insertion sort, which performs well on small input sizes.

By combining the strengths of these three algorithms, introsort achieves practical performance comparable to quicksort on typical data sets while maintaining the worst-case time complexity of O(n log n) thanks to the inclusion of heapsort. This makes introsort a reliable and versatile choice for sorting tasks.

Code implementation of the IntroSort algorithm in C++ (Iterative)

I2luY2x1ZGUgPGJpdHMvc3RkYysrLmg+CnVzaW5nIG5hbWVzcGFjZSBzdGQ7Cgp0ZW1wbGF0ZTx0eXBlbmFtZSBUPgp2b2lkIGluc2VydGlvblNvcnQodmVjdG9yPFQ+ICZhcnIsIGludCBsZWZ0LCBpbnQgcmlnaHQpIHsKZm9yIChpbnQgaSA9IGxlZnQgKyAxOyBpIDw9IHJpZ2h0OyBpKyspIHsKVCBrZXkgPSBhcnJbaV07CmludCBqID0gaSAtIDE7CndoaWxlIChqID49IGxlZnQgJiYgYXJyW2pdID4ga2V5KSB7CmFycltqICsgMV0gPSBhcnJbal07CmotLTt9CmFycltqICsgMV0gPSBrZXk7fQp9Cgp0ZW1wbGF0ZTx0eXBlbmFtZSBUPgppbnQgcGFydGl0aW9uKHZlY3RvcjxUPiAmYXJyLCBpbnQgbG93LCBpbnQgaGlnaCkgewpUIHBpdm90ID0gYXJyW2hpZ2hdOwppbnQgaSA9IChsb3cgLSAxKTsKZm9yIChpbnQgaiA9IGxvdzsgaiA8PSBoaWdoIC0gMTsgaisrKSB7CmlmIChhcnJbal0gPD0gcGl2b3QpIHsKaSsrOwpzd2FwKGFycltpXSwgYXJyW2pdKTsKfQp9CnN3YXAoYXJyW2kgKyAxXSwgYXJyW2hpZ2hdKTsKcmV0dXJuIChpICsgMSk7fQoKdGVtcGxhdGU8dHlwZW5hbWUgVD4Kdm9pZCBpbnRyb3NvcnRSZWN1cnNpdmUodmVjdG9yPFQ+ICZhcnIsIGludCBsb3csIGludCBoaWdoLCBpbnQgZGVwdGhMaW1pdCkgewppZiAobG93IDwgaGlnaCkgewppZiAoZGVwdGhMaW1pdCA9PSAwKSB7Cm1ha2VfaGVhcChhcnIuYmVnaW4oKSArIGxvdywgYXJyLmJlZ2luKCkgKyBoaWdoICsgMSk7CnNvcnRfaGVhcChhcnIuYmVnaW4oKSArIGxvdywgYXJyLmJlZ2luKCkgKyBoaWdoICsgMSk7Cn0gZWxzZSB7CmludCBwYXJ0aXRpb25JbmRleCA9IHBhcnRpdGlvbihhcnIsIGxvdywgaGlnaCk7CmludHJvc29ydFJlY3Vyc2l2ZShhcnIsIGxvdywgcGFydGl0aW9uSW5kZXggLSAxLCBkZXB0aExpbWl0IC0gMSk7CmludHJvc29ydFJlY3Vyc2l2ZShhcnIsIHBhcnRpdGlvbkluZGV4ICsgMSwgaGlnaCwgZGVwdGhMaW1pdCAtIDEpOwp9Cn0KfQoKdGVtcGxhdGU8dHlwZW5hbWUgVD4Kdm9pZCBpbnRyb3NvcnQodmVjdG9yPFQ+ICZhcnIpIHsKaW50IHNpemUgPSBhcnIuc2l6ZSgpOwppbnQgZGVwdGhMaW1pdCA9IDIgKiBsb2cyKHNpemUpOwppbnRyb3NvcnRSZWN1cnNpdmUoYXJyLCAwLCBzaXplIC0gMSwgZGVwdGhMaW1pdCk7Cmluc2VydGlvblNvcnQoYXJyLCAwLCBzaXplIC0gMSk7Cn0KCmludCBtYWluKCkgewp2ZWN0b3I8aW50PiBhcnIgPSB7OSwgNSwgMSwgNCwgM307CmNvdXQgPDwgIk9yaWdpbmFsIEFycmF5OiAiOwpmb3IgKGF1dG8gZTogYXJyKSBjb3V0IDw8IGUgPDwgIiAiOwoKaW50cm9zb3J0KGFycik7CmNvdXQgPDwgIlxuU29ydGVkIEFycmF5OiAiOwpmb3IgKGF1dG8gZTogYXJyKSBjb3V0IDw8IGUgPDwgIiAiOwoKcmV0dXJuIDA7Cn0=

Output:

Original Array: 9 5 1 4 3
Sorted Array: 1 3 4 5 9

Code explanation:

1. In this code, we first define an insertionSort() function, which implements the Insertion Sort algorithm.
2. The parameters this function takes are- a reference to a vector arr and the indices left and right to specify the range of elements to be sorted.
3. Next, we define a partition() function, which implements the partition step of the QuickSort algorithm. Its parameters are- a reference to a vector arr, along with the indices low and high to specify the range of elements to be partitioned.
4. We define another function called the introsortRecursive() function, which implements the recursive part of the Introsort algorithm. The function takes a reference to a vector arr, the indices low and high (they specify the range of elements to be sorted), and the depthLimit variable (to control the recursion depth) as parameters.
5. The introsort() function is defined next to implement the Introsort algorithm. It takes a reference to a vector arr as a parameter and calculates the depthLimit based on the array size. It then calls introsortRecursive to perform the sorting.
6. In the main() function, we declare and initialize an array arr, whose values are printed to the console using the cout command and a for loop. 
7. We then call the introsort() function to sort the array, after which the values are once again printed to the console.  

Time and Space complexity:

• Worst case: O(N log N)
• Average case: O(N log N)
• Best case: O(N log N)
• The auxiliary space required by the introsort algorithm is O(n) for the call stack when the naive quicksort algorithm is used.

Conclusion

Sorting algorithms play a vital role in programming, as they are utilized to solve a wide range of problems while optimizing the time complexity. This field of study encompasses extensive research and development efforts, with many individuals dedicated to enhancing these algorithms. Fortunately for developers, most programming languages provide pre-implemented sorting algorithms within their standard libraries.

• The sort function in C++ is a part of the STL library and allows us to perform sorting operations on a range of elements.
• It uses the IntroSort algorithm internally, providing a complexity of N*log(N), where N represents the number of elements in the range being sorted.
• We can define custom functions or lambda expressions to perform sorting based on specific requirements or conditions.
• For stable sorting, where equal elements maintain their relative order, the stable_sort() function in C++ is used. It ensures that elements with the same value retain their original order even after the sorting operation.
• In cases where we only need a partial sorting of the collection, the partial_sort() function comes into play.
• It rearranges the elements in the range such that the first part contains the smallest elements in ascending order, while the remaining elements are left without any specific order.

Also read- 51 C++ Interview Questions For Freshers & Experienced (With Answers)

Frequently Asked Questions

Q. How does the std::sort() function handle duplicate elements in the container?

The std::sort() function arranges the elements of the container in the specified order by default. When it encounters duplicate elements during the sorting process, the relative order of those duplicate elements is not guaranteed to be preserved.

The exact order of duplicate elements may vary depending on the specific implementation of the sort algorithm used by the C++ standard library. However, when the maintenance of the related order of elements is important, and the elements with duplicate sort keys are distinguishable based on other attributes, We should consider using the std::stable_sort() function in C++ for such cases.

Q. Can we use the sort() function on Linked lists or other non-random access data structures?

No! The standard sort function in C++ cannot be directly used on linked lists or other non-random access data structures. The sort function relies on random access iterators to efficiently rearrange elements in the container. We must iterate from the beginning and reach the desired position to access a particular position.

If we want to sort a linked list or other non-random access data structure, we have a few options, like using Insertion sort, Merge sort, and Quicksort. Choosing which sorting algorithm to use depends on the specific requirements of the application.

For example, if the linked list is small, then the insertion sort algorithm may be the most efficient algorithm to use. In contrast, if the linked list is large, then the merge sort or quicksort algorithm may be more efficient.

Q. Is it possible to sort elements based on multiple criteria using the sort() function in C++?

Yes, it is possible to sort the elements based on multiple criteria. All we need to do is define the appropriate custom comparator function that determines the order of elements during the sorting process. The comparator function should return true if the first element should be placed before the second element in the sorted sequence and false otherwise.

Here is an example that uses multiple criteria with the sort() function in C++:

Output:

Shivangi - 80
Shivani - 100
Shivani - 85
Shreeya - 85
Srishti - 95
Srishti - 91

Q. What is the difference between the sort function and the nth_element function?

The sort function in C++ and the nth_element function are both part of the C++ standard library's algorithm library and are used for sorting elements. However, they have different purposes and behaviors, as mentioned in the table below.

Q. Why do we need to learn different Sorting algorithms when the STL sort function is already available to us in C++?

Sorting algorithms continue to evolve, and new algorithms or variations are developed to address specific challenges. By staying updated with different algorithms, you can stay informed about new approaches that may offer improved efficiency or be a better fit for certain scenarios.

• Sorting is not just about obtaining a sorted result but also about improving time and space complexity.
• Different algorithms have their own strengths and weaknesses, and selecting the most efficient algorithm for a particular scenario can significantly impact performance.
• Apart from that, no single algorithm works best in all cases. It's important to understand the pros and cons of different algorithms to choose the most suitable one based on factors such as input size, data characteristics, and performance requirements.

Q. Are there any similar inbuilt sorting functions in languages other than C++?

Yes. Many programming languages provide built-in functions or methods similar to C++ std::sort(). A few instances of popular programming languages  with inbuilt sort functions are listed below:

1. Python: Python provides the built-in sorted() function, which returns a new sorted list from the given iterable or sequence. It also has the list.sort() method that sorts the list in-place.
2. Java: Java has the Arrays.sort() method for sorting arrays of primitive types and objects. It also provides the Collections.sort() method for sorting lists and other collection types.
3. JavaScript: JavaScript has the Array.prototype.sort() method that sorts the elements of an array in-place and returns the sorted array.
4. C#: C# provides the Array.Sort() method for sorting arrays of primitive types and objects. It also has the List<T>.Sort() method for sorting lists.
5. Ruby: Ruby offers the Array#sort method that sorts the elements of an array and returns a new sorted array. It also has the Array#sort! method for in-place sorting.

Q. Does the choice of pivot element affect the performance of IntroSort?

Yes, the choice of pivot element can affect the performance of IntroSort. The pivot element is the element around which the array is partitioned, and the performance of IntroSort depends on how well the pivot element divides the array.

• If the pivot element is chosen poorly, such as always selecting the first or last element, it can lead to an imbalanced partitioning, resulting in suboptimal performance.
• In the worst-case scenario, this can lead to quadratic time complexity, which is highly undesirable.
• However, if the pivot element is chosen well, then the array may be divided into two halves that are roughly equal in size. This can lead to a best-case scenario where IntroSort takes O(n log n) time to sort the array.

There are a few different strategies for choosing a pivot element. One common strategy is to choose the median of the array. This strategy is generally considered to be the best way to choose a pivot element, as it minimizes the chances of creating a very uneven partition.

Q. Can IntroSort handle user-defined comparison functions?

Yes, IntroSort can handle user-defined comparison functions. This means that we can use IntroSort to sort array elements that are compared using a custom comparison function.

By passing a user-defined element comparison function to the sort function, you can specify your own criteria for sorting the elements. The comparison function should take two arguments and return a bool value(using bool operator) indicating the relative order of the elements.

Q. Can we change the implementation of the sort() function in C++ from intro sort to some other sorting algorithms?

No, you cannot directly change the implementation of the sort() function in C++ from IntroSort to some other sorting algorithm. The C++ Standard Library determines the implementation of the sort() function, and it is typically based on IntroSort.

• The compiler and library implementers make the choice of using IntroSort in the implementation of the sort() function.
• This is because IntroSort offers a good balance of average-case performance and worst-case time complexity.
• It combines the benefits of quicksort, heapsort, and insertion sort to achieve efficient sorting.

Still, if you are determined enough to use a different sorting algorithm, you will have to implement it yourself or find a different library that provides the specific sorting algorithm you desire.

This compiles our discussion on the sort() function in C++. You might also be interested in reading the following:

1. Constructor In C++ & Its Types Explained (With Examples)
2. Static Member Function In C++ Explained With Proper Examples
3. Pure Virtual Function In C++ & Abstract Classes ( With Examples)
4. Function Prototype In C++ | Definition, Purpose & More (+Examples)
5. C++ Type Conversion & Type Casting Demystified (With Examples)