Python Program To Find LCM Of Two Numbers | 5 Methods With Examples

In mathematics, the concept of the Least Common Multiple (LCM) helps determine the smallest positive integer divisible by multiple numbers without any remainder. Calculating the LCM of two numbers is a common task in math and has multiple applications in programming. In this article, we will learn to find the LCM of two numbers in Python programming language. 

The simplicity and readability of Python language make it easy to create a program that tackles this mathematical problem efficiently. We can write a Python program to find the LCM of two numbers using basic coding concepts and Python's built-in functionalities. So, let's get started with the basics!

What Is LCM (Least Common Multiple)?

The Least Common Multiple (LCM) of two numbers is the smallest possible integer that is divisible by the given numbers. In other words, dividing the LCM by either of the two given numbers does not leave a remainder. In mathematics, the LCM of two numbers is denoted as LCM(a,b), where a and b are the two integers for which we need to find the Least Common Multiple. The method to find the LCM of two numbers is:

1. Firstly, find the prime factors of two numbers.
2. Next, in every case, write every number as a product of primes or matching primes vertically if possible.
3. Then, in each column, bring down all the primes and multiply the factors to get the LCM of those two numbers.

For example, say we want to find the LCM of 12 and 18. Then-

Prime factorization of 12: 2*2*3
Prime factorization of 18: 2*3*3

Now, when we write the matching primes vertically, we will get LCM(12,18): 2*2*3*3 = 36. Therefore, the LCM of 12 and 18 is 36.

How To Find The LCM Of Two Numbers In Python?

We use the Python math module to find the LCM of two numbers in Python. The math module in Python consists of many mathematical operations, of which the lcm() function is used to find the least common multiple of two integers. Let’s take a look at the basic approach/ algorithm to write a program to find the LCM of two numbers in Python:

• Step 1: From the math module, import the gcd function, which is used to calculate the LCM of two numbers.
• Step 2: Now define a function that is used to calculate LCM.
• Step 3: In this step, input any two numbers to find the LCM of them.
• Step 4: Next, with the given input numbers, call the LCM calculation function, i.e., lcm().
• Step 5: In the last step, display the results, which show the LCM of the given integers.

Below is a simple Python program that showcases how to apply the approach discussed above to find the LCM of two numbers. 

Code Example: 

# Import the gcd function from the math module
from math import gcd

# Function to calculate the LCM of two numbers
def lcm(x, y):
    # Calculate the product of the numbers
    product = x * y
    # Calculate the GCD (Greatest Common Divisor) of the numbers
    gcd_result = gcd(x, y)
    # Calculate the LCM using the formula: LCM = (x * y) / GCD(x, y)
    lcm_result = product // gcd_result
    return lcm_result

# Input from user for num1 & num2
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))

# Calculate the LCM
result = lcm(num1, num2)

# Display the LCM
print(f"The LCM of {num1} and {num2} is {result}")

Output:

Enter the first number: 20
Enter the second number: 100
The LCM of 20 and 100 is 100

Code Explanation:

In the sample Python program-

1. We begin by importing the gcd function from the math module, which is used to find the LCM of two numbers.
2. Next, we define an lcm() function, which takes x and y as function arguments. Inside the function-
• We calculate the product of those values and store it in the variable named product.
• Then, we call the gcd function with the two arguments x and y and then calculate the GCD(Greatest common divisor) of two numbers. Here, the result is stored in the variable named gcd_result.
• Next, we use results from previous steps to calculate the LCM of the two numbers and store the value in the variable lcm_result.
3. After that, we prompt the user to enter values using the input() function, convert the values into integer data type using the int() function and store them in variables num1 & num2, respectively.
4. We then call the lcm() function and pass the two input values to it. The result is then stored in the variable called result.
5. Finally, we use the print function to output the LCM (Least Common Multiple) of the two integers on the output screen.

This approach provides a simple solution to find the LCM of two numbers in Python. The math module is a rich library that offers multiple other functions to carry out various manipulations on data/ variables in Python. 

Find LCM Of Two Numbers In Python Using For Loop

We can use the for loop construct to write a Python program to find the LCM of two numbers. This approach systematically determines the least common multiple (LCM) of the given numbers.

• Within the Python program, a for loop iterates through a range of numbers, starting from the larger of the two input numbers and moving up to and including the product of the two numbers.
• At each iteration, the program checks if the current number is divisible by both input numbers without leaving a remainder.
• This check is performed using the modulo operator (%). If the current number satisfies this condition, it is identified as the LCM, and the program returns this value.

Now, let's look at the syntax and a Python program sample where we find the LCM of two numbers in Python language using a for loop.

Syntax:

for i in range(larger, x * y + 1):
    if i % x == 0 and i % y == 0:
        return i

Code Example:

# Function to calculate the LCM of two numbers
def lcm(x, y):
    # Find the larger of the two numbers
    larger = max(x, y)
        for i in range(larger, x * y + 1):
        if i % x == 0 and i % y == 0:
            return i

# Prompting the user to input values for num1 & num2
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))

# Calculate the LCM
result = lcm(num1, num2)

# Display the LCM
print(f"The LCM of {num1} and {num2} is {result}")

Output:

Enter the first number: 3
Enter the second number: 18
The LCM of 3 and 18 is 18

Code Explanation:

In this sample Python code-

1. We define the lcm() function, which takes two variables, x and y, as input and calculates their LCM. Inside the function definition-
   • We use the max() function to find the largest of two numbers and store it in the variable called larger. 
   • Then, we initiate a for loop to iterate a range of numbers using the range() function.
   • The loop control variable initially starts from the larger variable and continues until its value is equal to the product of x and y plus 1, i.e., x*y +1. 
   • In every iteration of the for loop, the if-statement inside it checks if the remainder of the loop variable divided by x as well as y is zero.
   • For this, we use the module operator to perform division, then the relational equality operator to check equality with zero, and finally, the logical AND operator to connect the two expressions. 
   • If the statement condition is true, i.e., i % x == 0 and i % y == 0 return true, then the if-statement returns i, the LCM of the two numbers to the loop.
   • If the condition is false, the iteration continues until the LCM is found and the condition is satisfied.
2. After defining the function to find the LCM of two numbers, we prompt the user to input two values using the input() function and a string message.
3. We convert the value provided to integer type using the int() function and store them in variables num1 & num2, respectively. 
4. Following this, we call the lcm() function with the num1 and num2 as arguments. The function finds the LCM, and the outcome is stored in the variable result.
5. In the final step, we display the LCM of the two numbers to the console using the print() function with formatted string where interpolation {} is the placeholder of integer values.

Time Complexity: This function has a time complexity of O(x * y - max(x, y)), which depends upon the corresponding values of x and y. 

Using While Loop To Find LCM Of Two Numbers In Python

In this method, we use a while loop to calculate the Greatest Common Divisor (GCD) and the Least Common Multiple (LCM) of two given numbers without relying on imported libraries. This method enables us to derive the GCD and subsequently compute the LCM by iteratively checking and computing the necessary values through a logical and iterative process.

Given below is the syntax of the while loop when we want to find the LCM of two numbers in Python, followed by an example Python program that gives the code implementation of the same.

Syntax:

while true:
    process=do_something()
    if progress is done:
        break

Code Example:

# Function to calculate the LCM of two numbers
def lcm_with_gcd(x, y):
    a, b = x, y
    while b:
        a, b = b, a % b
        gcd_result = a
        lcm_result = (x * y) // gcd_result
        return lcm_result

# Prompting user to input num1
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))

# Calculate the LCM using GCD
result = lcm_with_gcd(num1, num2)

# Display the LCM
print(f"The LCM of {num1} and {num2} is {result}")

Output:

Enter the first number: 10
Enter the second number: 100
The LCM of 10 and 100 is 100

Code Explanation:

In the example Python code-

1. We begin by defining a function called lcm_with_gcd(), which takes two integer values and calculates the LCM of two numbers and the GCD.
2. Inside the function, we assign the values of x and y to a and b. These are the variables that are used to calculate the GCD of two numbers.
3. Next, we employ a while loop to find GCD using the Euclidean algorithm. The loop continues to iterate until the smallest number becomes zero.
   • In every iteration, we assign the value of a to b and the remainder of the division of a by b to variable b.
   • The iterations continue till the smallest number(b) becomes zero, at which point the value of a is the GCD  of the two numbers. This is then stored in the variable named gcd_result.
4. After that, we use the value of the GCD in the basic formula for LCM, i.e., [LCM = (x * y) /GCD(x, y)], to find the LCM of the two numbers in the Python program.  
5. The outcome of this calculation is stored in the lcm_result variable, which is returned by the loop and, subsequently, the function. 
6. Moving to the main application part of the code, we prompt the user to enter the input two values using input(), convert them to integers using int() and store them in the respective variables.
7. Next, we call the lcm() function with those two given input values and then the final result will be stored in the variable result.
8. Lastly, we use the print() function to display the values of the input variables and the LCM of the two numbers.

Time Complexity: O(log(min(x, y))). Here, the time complexity is due to the efficient algorithm used by the gcd() function, which was more time-consuming.
Space complexity: O(1): By using the constant amount of memory, it has a space complexity of O(1).

The Recursive Function To Find LCM Of Two Numbers In Python

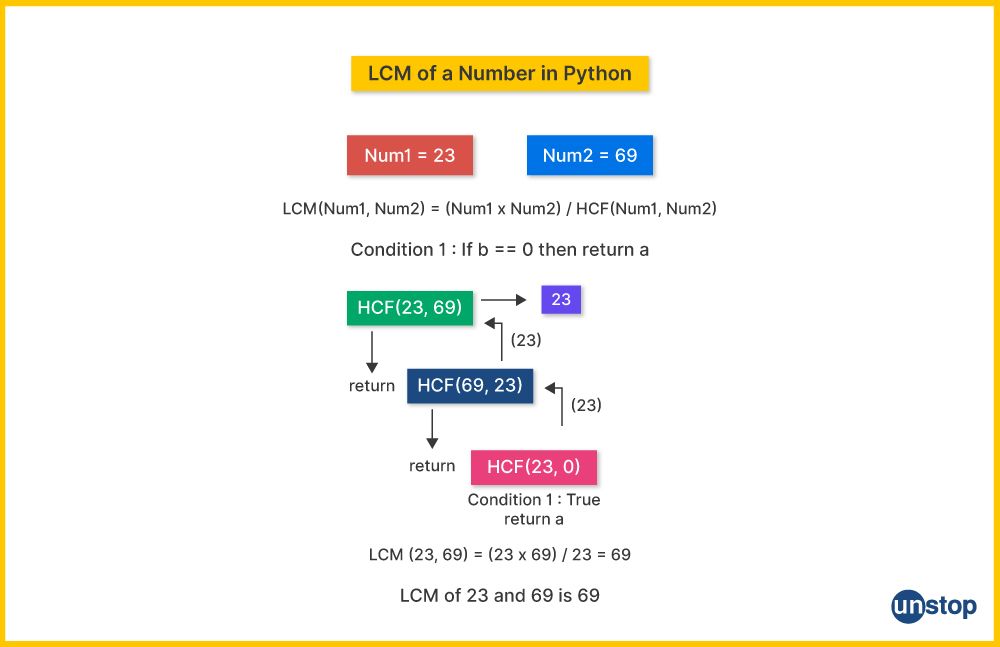
A recursive function is a special kind of function that recursively calls itself until a desired result is obtained. We can use a recursive function to compute both the Greatest Common Divisor (GCD) and the Least Common Multiple (LCM) of two specified numbers without relying on imported libraries. 

Syntax:

def function_name(parameters):
   # Base case: condition to end the recursion
   if base_case_condition:
      return base_case_value
   else:
      return function_name(modified_parameters)

Given above is the syntax of a recursion function to find the LCM of two numbers in Python. And below is a Python program example showcasing the implementation of the same.

Code Example:

# Recursive function to calculate the GCD of two numbers
def gcd_recursive(x, y):
    if y == 0:
        return x
    else:
        return gcd_recursive(y, x % y)

# Function to calculate the LCM of two numbers using GCD
def lcm_with_gcd_recursive(x, y):
    gcd_result = gcd_recursive(x, y)
    lcm_result = (x * y) // gcd_result
    return lcm_result

# Prompting for user input num1
num1 = int(input("Enter the first number: "))
# Prompting for user input num2
num2 = int(input("Enter the second number: "))

# Calculate the LCM using GCD
result = lcm_with_gcd_recursive(num1, num2)

# Display the LCM
print(f"The LCM of {num1} and {num2} is {result}")

Output:

Enter the first number: 2
Enter the second number: 6
The LCM of 2 and 6 is 6

Code Explanation:

In the Python code example-

1. We first define a recursive function gcd_recursive() used to calculate the GCD of two numbers, x and y. 
   • The recursive function contains an if-else statement where the if condition checks the equality of y with zero. If the condition y==0 is true, then the function returns the value of x value as GCD.
   • If not, then the function is recursively called again with variable x and the remainder of the division of x by y as arguments. The else-code block is implemented until the if-condition is satisfied and the GCD is found.
2. After that, we define a recursive function of lcm_with_gcd_recursive(x, y), which calculates the LCM of the value of two numbers.
   • Inside this function, we first call the gcd_recursive() function to calculate the GCD of input variables x and y and the outcome is stored in the gcd_result variable.
   • Then, we use the gcd_result variable and apply it to the LCM formula to calculate the LCM of the two numbers. 
   • The outcome of this calculation is stored in the lcm_result variable, which the function returns.
3. Moving to the main part, we prompt the user to enter the input two values which are stored in the variables named num1 and num2, respectively.
4. Following this, we call the lcm_with_gcd_recursive() function with user-provided variables as arguments.
5. The function calculates the GCD and, subsequently, the LCM of the two numbers and returns the value stored inside the lcm_result variable.
6. Finally, we use the print() function with f-strings to display the original input numbers and their LCM to the console. 

Time Complexity: O(log(min(x, y))), i.e., due to the use of the Euclidean algorithm in the recursion process, recursive GCD calculations are more time-consuming.
Space complexity: O(log(min(x, y))). In addition, the space complexity for a recursive call depends on its depth.

The gcd() Function To Find LCM Of Two Numbers In Python

The gcd() function belongs to the math module in Python, and its purpose is to compute the Greatest Common Divisor (GCD) of input numbers. The gcd() function provides a convenient solution for determining the GCD of two numbers without extensive manual implementation. Just like in some other approaches to find the LCM of two numbers in Python, we then use the GCD calculated to get the LCM of the input numbers.

Syntax:

from math import gcd
result = gcd(number1, number2)

Here, we first import the math module and then use the gcd() function with number1 and number2 as parameters. Given below is an illustrative Python program example that finds the LCM of two numbers using the gcd() function.

Code Example:

#Importing the gcd() function from the math module
from math import gcd

#Defining the 
def lcm(a, b):
    return (a * b) // gcd(a, b)

#Example implementation
number1 = 12
number2 = 20
result = lcm(number1, number2)
print("LCM of", number1, "and", number2, "is:", result)

Program Output:

LCM of 12 and 20 is: 60

Code Explanation:

In the Python code sample-

1. We begin by importing the gcd() function directly from the math module, which is a part of the Python library. This facilitates our computation related to the Greatest Common Divisor (GCD).
2. Following the import statement, we define a function named lcm(a, b). This function is designed to calculate the Least Common Multiple (LCM) of two given numbers, a and b.
3. Inside the function, we employ the gcd() function, passing a and b as arguments, to determine their GCD. This value is utilized in the subsequent computation.
4. The function applies the GCD to the basic LCM formula, LCM = (a * b) / GCD, computes the LCM of the two numbers a and b, and returns the LCM value.
5. In the example implementation section, we initialize two variables number1 and number2, with the values 12 and 20, respectively.
6. We then invoke the lcm() function with number1 and number2 as arguments. This function effectively calculates the LCM of the provided numbers and stores the result in the variable result.
7. Finally, we print a message to the output console indicating the LCM of number1 and number2, along with the calculated result using the print() function.

Time Complexity: The time complexity of the provided code is O(log min(a, b)), where 'a' and 'b' are the input parameters to the lcm() function.
Space complexity: The space complexity of the provided code is O(1).

Find LCM Of Two Numbers In Python Using The lcm() Function

Just like the gcd() function, the lcm() function is also an in-built function within the rich math module of Python libraries. As the name suggests, the primary purpose of the lcm() function is to calculate the Least Common Multiple (LCM) of argument numbers.

Other Python libraries like NumPy and SymPy also have methods to calculate the LCM of two numbers. However, in this approach, we will use the lcm() function to get the desired results.

Syntax:

from math import gcd
outcome = math.lcm(parameters)

In the syntax above, we import the math module and use the lcm() function. The term outcome refers to the variable that will hold the LCM of the parameters that represent the input numbers. Let's look at a Python program example to calculate the LCM of the provided arguments using the lcm() function.

Code Example:

# Importing the math module 
import math

# Input two numbers from the user
num1 = int(input("Enter the first number: "))
num2 = int(input("Enter the second number: "))

# Calculate the LCM using the lcm() function
result = math.lcm(num1, num2)

# Display the LCM
print(f"The LCM of {num1} and {num2} is {result}")

Output:

Enter the first number: 4
Enter the second number: 8
The LCM of 4 and 8 is 8

Code Explanation:

In this Python example program-

1. We first import the math module, which contains the lcm() function.
2. Then, we prompt the user to provide values for two variables, num1 and num2, using the input() function. The values are stored in the respective variable after conversion to integer type with the int() function.
3. Following this, we use the period/ dot notation to access the lcm() function from the math module. 
4. We pass the variables num1 and num2 as arguments when calling the lcm() function. The function calculates the LCM for the two numbers, and its outcome is stored in the result variable.
5. Lastly, we display the LCM to the console using the print() function with formatted strings.

Time Complexity: O(log min(a, b))
Space complexity: O(1)

Comparison Of Complexities Of Programs To Find LCM Of Two Numbers In Python

Complexity analysis in Python involves evaluating algorithms based on their time and space requirements. Time complexity measures how an algorithm's performance scales with input size, while space complexity evaluates its memory usage.

In the table below, we have provided a comparison of these complexities for the various approaches we used to find LCM of two numbers in Python programs.

Conclusion

In this article, we've covered a variety of approaches we can follow to find the LCM of two numbers in Python. The basic approach to find the LCM is to first calculate the GCD and then use that with the LCM formula to calculate the desired value. While the basic approach might be the same, the techniques/ constructs used differ. These include the basic formula for loop, while loop, recursive function, and in-built functions like gcd() and lcm() belonging to the math module. Using these approaches gives us several tools to deal with complex calculations and resolve a wide range of mathematical and programming problems.

Frequently Asked Questions

Q. What is the relationship between GCD and LCM?

The relationship between the Greatest Common Divisor (GCD) and Least Common Multiple (LCM) of two integers is defined by the following equation:

LCM(a, b) = (a * b) / GCD(a, b)

This equation essentially states that the LCM of two numbers can be obtained by dividing the product of the two numbers by their GCD. Here-

• LCM(a, b) represents the Least Common Multiple of integers 'a' and 'b'.
• GCD(a, b) represents the Greatest Common Divisor of integers 'a' and 'b'.

This relationship is based on the fundamental property that the product of two numbers is equal to the product of their GCD and LCM. Therefore, by rearranging this property, we can derive the equation above, which provides a straightforward way to calculate the LCM when the GCD is known.

Q. What are the different approaches to finding the LCM of two numbers in Python? Which approach would you choose for efficiency?

We can use several approaches to find the LCM of two numbers in Python. Here are three common methods:

1. Prime Factorization Method: In this approach, you factorize both numbers into their prime factors and then take the product of the highest power of each prime factor present in either number. For example, if the prime factorization of the two numbers is:

num1 = 2^2 * 3 * 5
num2 = 2 * 3^2 * 7

Then, the LCM would be: LCM(num1, num2) = 2^2 * 3^2 * 5 * 7.

2. Using the GCD (Greatest Common Divisor): The LCM of two numbers can be calculated using their GCD. The formula for computing LCM using GCD is: LCM(a, b) = (a * b) / GCD(a, b).

3. Using the math.lcm() Function: Python's math module provides a built-in function called lcm() that directly computes the LCM of two or more integers.

Efficiency Considerations: For efficiency, the second approach, using the GCD, is preferred in most cases. It offers a balance between simplicity and computational complexity.

Q. What are the common applications of finding LCM in Python programming?

Finding the Least Common Multiple (LCM) of numbers in Python programming has various applications across different domains. Some common applications include:

1. Fraction Operations: In arithmetic operations involving fractions, it's often necessary to find a common denominator to perform addition, subtraction, or comparison. LCM helps in determining the least common denominator, making fraction operations easier and more efficient.
2. Time Complexity Analysis: In algorithm design and analysis, particularly in the study of time complexity, finding the LCM of numbers can help in determining the overall time complexity of algorithms with nested loops or recursive calls. 
3. Scheduling and Periodicity: In scheduling algorithms or systems that involve periodic tasks or events, finding the LCM of task periods or event frequencies is essential. 
4. Cryptography and Security: In cryptography and security protocols, LCM calculations are used in various cryptographic algorithms, such as RSA encryption and key exchange protocols. 
5. Computational Mathematics: In computational mathematics and number theory, finding the LCM of numbers is fundamental to solving various problems, such as finding common multiples, solving linear Diophantine equations, and exploring patterns in sequences or series.

Q. Can you optimize the computation of LCM for large numbers or multiple inputs?

Yes, we can optimize the computation of LCM for large numbers or multiple inputs using various techniques. One approach is to reduce redundant computations by exploiting the distributive property of LCM and utilizing efficient algorithms for calculating the Greatest Common Divisor (GCD). By iteratively applying the distributive property, the number of pairwise LCM computations can be minimized.

Q. What is the LCM of 60 and 75?

We can find the LCM of two numbers in Python, as shown in the code example below.

Code Example:

from math import gcd

# Function to calculate LCM using GCD
def lcm(x, y):
    return abs(x * y) // gcd(x, y)

# Numbers for LCM calculation
num1 = 60
num2 = 75

# Calculate LCM
lcm_result = lcm(num1, num2)

# Display the result
print(f"The LCM of {num1} and {num2} is {lcm_result}")

Output:

The LCM of 60 and 76 is 300

By now, you can surely write a program to find the LCM of two numbers in Python. Here are a few other interesting topics you must know:

1. Python Bitwise Operators | Positive & Negative Numbers (+Examples)
2. 12 Ways To Compare Strings In Python Explained (With Examples)
3. Python IDLE | The Ultimate Beginner's Guide With Images & Codes!
4. Python String.Replace() And 8 Other Ways Explained (+Examples)
5. Difference Between List And Tuple In Python With Examples