- What Is Python? An Introduction
- What Is The History Of Python?
- Key Features Of The Python Programming Language
- Who Uses Python?
- Basic Characteristics Of Python Programming Syntax
- Why Should You Learn Python?
- Applications Of Python Language
- Advantages And Disadvantages Of Python
- Some Useful Python Tips & Tricks For Efficient Programming
- Python 2 Vs. Python 3: Which Should You Learn?
- Python Libraries
- Conclusion
- Frequently Asked Questions
- It's Python Basics Quiz Time!
- What is Python & its Brief History
- Key Features of Python Programming Language
- Applications of Python Language
- Practical Python Code Examples
- About Python IDLE
- Comparative Features of Python, Java, & C++
- Conclusion
- Frequently Asked Questions
- Take A Quiz To Rehash Python's Features!
- What Is Python IDLE?
- What Is Python Shell & Its Uses?
- Primary Features Of Python IDLE
- How To Use Python IDLE Shell? Setting Up Your Python Environment
- How To Work With Files In Python IDLE?
- How To Execute A File In Python IDLE?
- Improving Workflow In Python IDLE Software
- Debugging In Python IDLE
- Customizing Python IDLE
- Code Examples
- Conclusion
- Frequently Asked Questions (FAQs)
- How Well Do You Know IDLE? Take A Quiz!
- What Is A Variable In Python?
- Creating And Declaring Python Variables
- Rules For Naming Python Variables
- How To Print Python Variables?
- How To Delete A Python Variable?
- Various Methods Of Variables Assignment In Python
- Python Variable Types
- Python Variable Scope
- Concatenating Python Variables
- Object Identity & Object References Of Python Variables
- Reserved Words/ Keywords & Python Variable Names
- Conclusion
- Frequently Asked Questions
- Rehash Python Variables Basics With A Quiz!
- What Is A String In Python?
- Creating String In Python
- How To Create Multiline Python Strings?
- Reassigning Python Strings
- Accessing Characters Of Python Strings
- How To Update Or Delete A Python String?
- Reversing A Python String
- Formatting Python Strings
- Concatenation & Comparison Of Python Strings
- Python String Operators
- Python String Functions
- Escape Sequences In Python Strings
- Conclusion
- Frequently Asked Questions
- Rehash Python Strings Basics With A Quiz!
- What Is Python Namespace?
- Lifetime Of Python Namespace
- Types Of Python Namespace
- The Built-In Namespace In Python
- The Global Namespace In Python
- The Local Namespace In Python
- The Enclosing Namespace In Python
- Variable Scope & Namespace In Python
- Python Namespace Dictionaries
- Changing Variables Out Of Their Scope & Python Namespace
- Best Practices Of Python Namespace
- Conclusion
- Frequently Asked Questions
- Test Your Knowledge Of Python Namespaces!
- What Are Logical Operators In Python?
- The AND Python Logical Operator
- The OR Python Logical Operator
- The NOT Python Logical Operator
- Short-Circuiting Evaluation Of Python Logical Operators
- Precedence of Logical Operators In Python
- How Does Python Calculate Truth Value?
- Final Note On How AND & OR Python Logical Operators Work
- Conclusion
- Frequently Asked Questions
- Python Logical Operators Quiz– Test Your Knowledge!
- What Are Bitwise Operators In Python?
- List Of Python Bitwise Operators
- AND Python Bitwise Operator
- OR Python Bitwise Operator
- NOT Python Bitwise Operator
- XOR Python Bitwise Operator
- Right Shift Python Bitwise Operator
- Left Shift Python Bitwise Operator
- Python Bitwise Operations On Negative Integers
- The Binary Number System
- Application of Python Bitwise Operators
- Python Bitwise Operator Overloading
- Conclusion
- Frequently Asked Questions
- Test Your Knowledge Of Python Bitwise Operators!
- What Is The Print() Function In Python?
- How Does The print() Function Work In Python?
- How To Print Single & Multi-line Strings In Python?
- How To Print Built-in Data Types In Python?
- Print() Function In Python For Values Stored In Variables
- Print() Function In Python With sep Parameter
- Print() Function In Python With end Parameter
- Print() Function In Python With flush Parameter
- Print() Function In Python With file Parameter
- How To Remove Newline From print() Function In Python?
- Use Cases Of The print() Function In Python
- Understanding Print Statement In Python 2 Vs. Python 3
- Conclusion
- Frequently Asked Questions
- Know The print() Function In Python? Take A Quiz!
- Working Of Normal Print() Function
- The New Line Character In Python
- How To Print Without Newline In Python | Using The End Parameter
- How To Print Without Newline In Python 2.x? | Using Comma Operator
- How To Print Without Newline In Python 3.x?
- How To Print Without Newline In Python With Module Sys
- The Star Pattern(*) | How To Print Without Newline & Space In Python
- How To Print A List Without Newline In Python?
- How To Remove New Lines In Python?
- Conclusion
- Frequently Asked Questions
- Think You Can Print Without a Newline in Python? Prove It!
- What Is A Python For Loop?
- How Does Python For Loop Work?
- When & Why To Use Python For Loops?
- Python For Loop Examples
- What Is Rrange() Function In Python?
- Nested For Loops In Python
- Python For Loop With Continue & Break Statements
- Python For Loop With Pass Statement
- Else Statement In Python For Loop
- Conclusion
- Frequently Asked Questions
- Think You Know Python's For Loop? Prove It!
- What Is Python While Loop?
- How Does The Python While Loop Work?
- How To Use Python While Loops For Iterations?
- Control Statements In Python While Loop With Examples
- Python While Loop With Python List
- Infinite Python While Loop in Python
- Python While Loop Multiple Conditions
- Nested Python While Loops
- Conclusion
- Frequently Asked Questions
- Mastered Python While Loop? Let’s Find Out!
- What Are Conditional If-Else Statements In Python?
- Types Of If-Else Statements In Python
- If Statement In Python
- If-Else Statement In Python
- Nested If-Else Statement In Python
- Elif Statement In Python
- Ladder If-Elif-Else Statement In Python
- Short Hand If-Statement In Python
- Short Hand If-Else Statement In Python
- Operators & If-Esle Statement In Python
- Other Statements With If-Else In Python
- Conclusion
- Frequently Asked Questions
- Quick If-Else Statement Quiz– Let’s Go!
- What Is Control Structure In Python?
- Types Of Control Structures In Python
- Sequential Control Structures In Python
- Decision-Making Control Structures In Python
- Repetition Control Structures In Python
- Benefits Of Using Control Structures In Python
- Conclusion
- Frequently Asked Questions
- Control Structures in Python – Are You the Master? Take A Quiz!
- What Are Python Libraries?
- How Do Python Libraries Work?
- Standard Python Libraries (With List)
- Important Python Libraries For Data Science
- Important Python Libraries For Machine & Deep Learning
- Other Important Python Libraries You Must Know
- Working With Third-Party Python Libraries
- Troubleshooting Common Issues For Python Libraries
- Python Libraries In Larger Projects
- Importance Of Python Libraries
- Conclusion
- Frequently Asked Questions
- Quick Quiz On Python Libraries – Let’s Go!
- What Are Python Functions?
- How To Create/ Define Functions In Python?
- How To Call A Python Function?
- Types Of Python Functions Based On Parameters & Return Statement
- Rules & Best Practices For Naming Python Functions
- Basic Types of Python Functions
- The Return Statement In Python Functions
- Types Of Arguments In Python Functions
- Docstring In Python Functions
- Passing Parameters In Python Functions
- Python Function Variables | Scope & Lifetime
- Advantages Of Using Python Functions
- Recursive Python Function
- Anonymous/ Lambda Function In Python
- Nested Functions In Python
- Conclusion
- Frequently Asked Questions
- Python Functions – Test Your Knowledge With A Quiz!
- What Are Python Built-In Functions?
- Mathematical Python Built-In Functions
- Python Built-In Functions For Strings
- Input/ Output Built-In Functions In Python
- List & Tuple Python Built-In Functions
- File Handling Python Built-In Functions
- Python Built-In Functions For Dictionary
- Type Conversion Python Built-In Functions
- Basic Python Built-In Functions
- List Of Python Built-In Functions (Alphabetical)
- Conclusion
- Frequently Asked Questions
- Think You Know Python Built-in Functions? Prove It!
- What Is A round() Function In Python?
- How Does Python round() Function Work?
- Python round() Function If The Second Parameter Is Missing
- Python round() Function If The Second Parameter Is Present
- Python round() Function With Negative Integers
- Python round() Function With Math Library
- Python round() Function With Numpy Module
- Round Up And Round Down Numbers In Python
- Truncation Vs Rounding In Python
- Practical Applications Of Python round() Function
- Conclusion
- Frequently Asked Questions
- Revisit Python’s round() Function – Take The Quiz!
- What Is Python pow() Function?
- Python pow() Function Example
- Python pow() Function With Modulus (Three Parameters)
- Python pow() Function With Complex Numbers
- Python pow() Function With Floating-Point Arguments And Modulus
- Python pow() Function Implementation Cases
- Difference Between Inbuilt-pow() And math.pow() Function
- Conclusion
- Frequently Asked Questions
- Test Your Knowledge Of Python’s pow() Function!
- Python max() Function With Objects
- Examples Of Python max() Function With Objects
- Python max() Function With Iterable
- Examples Of Python max() Function With Iterables
- Potential Errors With The Python max() Function
- Python max() Function Vs. Python min() Functions
- Conclusion
- Frequently Asked Questions
- Think You Know Python max() Function? Take A Quiz!
- What Are Strings In Python?
- What Are Python String Methods?
- List Of Python String Methods For Manipulating Case
- List Of Python String Methods For Searching & Finding
- List Of Python String Methods For Modifying & Transforming
- List Of Python String Methods For Checking Conditions
- List Of Python String Methods For Encoding & Decoding
- List Of Python String Methods For Stripping & Trimming
- List Of Python String Methods For Formatting
- Miscellaneous Python String Methods
- List Of Other Python String Operations
- Conclusion
- Frequently Asked Questions
- Mastered Python String Methods? Take A Quiz!
- What Is Python String?
- The Need For Python String Replacement
- The Python String replace() Method
- Multiple Replacements With Python String.replace() Method
- Replace A Character In String Using For Loop In Python
- Python String Replacement Using Slicing Method
- Replace A Character At a Given Position In Python String
- Replace Multiple Substrings With The Same String In Python
- Python String Replacement Using Regex Pattern
- Python String Replacement Using List Comprehension & Join() Method
- Python String Replacement Using Callback With re.sub() Method
- Python String Replacement With re.subn() Method
- Conclusion
- Frequently Asked Questions
- Know How To Replace Python Strings? Prove It!
- What Is String Slicing In Python?
- How Indexing & String Slicing Works In Python
- Extracting All Characters Using String Slicing In Python
- Extracting Characters Before & After Specific Position Using String Slicing In Python
- Extracting Characters Between Two Intervals Using String Slicing In Python
- Extracting Characters At Specific Intervals (Step) Using String Slicing In Python
- Negative Indexing & String Slicing In Python
- Handling Out-of-Bounds Indices In String Slicing In Python
- The slice() Method For String Slicing In Python
- Common Pitfalls Of String Slicing In Python
- Real-World Applications Of String Slicing
- Conclusion
- Frequently Asked Questions
- Quick Python String Slicing Quiz– Let’s Go!
- Introduction To Python List
- How To Create A Python List?
- How To Access Elements Of Python List?
- Accessing Multiple Elements From A Python List (Slicing)
- Access List Elements From Nested Python Lists
- How To Change Elements In Python Lists?
- How To Add Elements To Python Lists?
- Delete/ Remove Elements From Python Lists
- How To Create Copies Of Python Lists?
- Repeating Python Lists
- Ways To Iterate Over Python Lists
- How To Reverse A Python List?
- How To Sort Items Of Python Lists?
- Built-in Functions For Operations On Python Lists
- Conclusion
- Frequently Asked Questions
- Revisit Python Lists Basics With A Quick Quiz!
- What Is List Comprehension In Python?
- Incorporating Conditional Statements With List Comprehension In Python
- List Comprehension In Python With range()
- Filtering Lists Effectively With List Comprehension In Python
- Nested Loops With List Comprehension In Python
- Flattening Nested Lists With List Comprehension In Python
- Handling Exceptions In List Comprehension In Python
- Common Use Cases For List Comprehensions
- Advantages & Disadvantages Of List Comprehension In Python
- Best Practices For Using List Comprehension In Python
- Performance Considerations For List Comprehension In Python
- For Loops & List Comprehension In Python: A Comparison
- Difference Between Generator Expression & List Comprehension In Python
- Conclusion
- Frequently Asked Questions
- Rehash Python List Comprehension Basics With A Quiz!
- What Is A List In Python?
- How To Find Length Of List In Python?
- For Loop To Get Python List Length (Naive Approach)
- The len() Function To Get Length Of List In Python
- The length_hint() Function To Find Length Of List In Python
- The sum() Function To Find The Length Of List In Python
- The enumerate() Function To Find Python List Length
- The Counter Class From collections To Find Python List Length
- The List Comprehension To Find Python List Length
- Find The Length Of List In Python Using Recursion
- Comparison Between Ways To Find Python List Length
- Conclusion
- Frequently Asked Questions
- Know How To Get Python List Length? Prove it!
- List of Methods To Reverse A Python List
- Python Reverse List Using reverse() Method
- Python Reverse List Using the Slice Operator ([::-1])
- Python Reverse List By Swapping Elements
- Python Reverse List Using The reversed() Function
- Python Reverse List Using A for Loop
- Python Reverse List Using While Loop
- Python Reverse List Using List Comprehension
- Python Reverse List Using List Indexing
- Python Reverse List Using The range() Function
- Python Reverse List Using NumPy
- Comparison Of Ways To Reverse A Python List
- Conclusion
- Frequently Asked Questions
- Time To Test Your Python List Reversal Skills!
- What Is Indexing In Python?
- The Python List index() Function
- How To Use Python List index() To Find Index Of A List Element
- The Python List index() Method With Single Parameter (Start)
- The Python List index() Method With Start & Stop Parameters
- What Happens When We Use Python List index() For An Element That Doesn't Exist
- Python List index() With Nested Lists
- Fixing IndexError Using The Python List index() Method
- Python List index() With Enumerate()
- Real-world Examples Of Python List index() Method
- Difference Between find() And index() Method In Python
- Conclusion
- Frequently Asked Questions
- Think You Know Python List Indexing? Take A Quiz!
- How To Remove Elements From List In Python?
- The remove() Method To Remove Element From Python List
- The pop() Method To Remove Element From List In Python
- The del Keyword To Remove Element From List In Python
- The clear() Method To Remove Elements From Python List
- List Comprehensions To Conditionally Remove Element From List In Python
- Key Considerations For Removing Elements From Python Lists
- Why We Need to Remove Elements From Python List
- Performance Comparison Of Methods To Remove Element From List In Python
- Conclusion
- Frequently Asked Questions
- Quiz– Prove You Know How To Remove Item From Python Lists!
- How To Remove Duplicates From A List In Python?
- The set() Function To Remove Duplicates From Python List
- Remove Duplicates From Python List Using For Loop
- Using List Comprehension Remove Duplicates From Python List
- Remove Duplicates From Python List Using enumerate() With List Comprehension
- Dictionary & fromkeys() Method To Remove Duplicates From Python List
- Remove Duplicates From Python List Using in, not in Operators
- Remove Duplicates From Python List Using collections.OrderedDict.fromkeys()
- Remove Duplicates From Python List Using Counter with freq.dist() Method
- The del Keyword Remove Duplicates From Python List
- Remove Duplicates From Python List Using DataFrame
- Remove Duplicates From Python List Using pd.unique and np.unipue
- Remove Duplicates From Python List Using reduce() function
- Comparative Analysis Of Ways To Remove Duplicates From Python List
- Conclusion
- Frequently Asked Questions
- Think You Know How to Remove Duplicates? Take A Quiz!
- What Is Python List & How To Access Elements?
- What Is IndexError: List Index Out Of Range & Its Causes In Python?
- Understanding Indexing Behavior In Python Lists
- How to Prevent/ Fix IndexError: List Index Out Of Range In Python
- Handling IndexError Gracefully Using Try-Except
- Debugging Tips For IndexError: List Index Out Of Range Python
- Conclusion
- Frequently Asked Questions
- Avoiding ‘List Index Out of Range’ Errors? Take A Quiz!
- What Is the Python sort() List Method?
- Sorting In Ascending Order Using The Python sort() List Method
- How To Sort Items In Descending Order Using Python sort() List Method
- Custom Sorting Using The Key Parameter Of Python sort() List Method
- Examples Of Python sort() List Method
- What Is The sorted() List Method In Python
- Differences Between sorted() And sort() List Methods In Python
- When To Use sorted() & When To Use sort() List Method In Python
- Conclusion
- Frequently Asked Questions
- Take A Quick Python's sort() Quiz!
- What Is A List In Python?
- What Is A String In Python?
- Why Convert Python List To String?
- How To Convert List To String In Python?
- The join() Method To Convert Python List To String
- Convert Python List To String Through Iteration
- Convert Python List To String With List Comprehension
- The map() Function To Convert Python List To String
- Convert Python List to String Using format() Function
- Convert Python List To String Using Recursion
- Enumeration Function To Convert Python List To String
- Convert Python List To String Using Operator Module
- Python Program To Convert String To List
- Conclusion
- Frequently Asked Questions
- Convert Lists To Strings Like A Pro! Take A Quiz
- What Is Inheritance In Python?
- Python Inheritance Syntax
- Parent Class In Python Inheritance
- Child Class In Python Inheritance
- The __init__() Method In Python Inheritance
- The super() Function In Python Inheritance
- Method Overriding In Python Inheritance
- Types Of Inheritance In Python
- Special Functions In Python Inheritance
- Advantages & Disadvantages Of Inheritance In Python
- Common Use Cases For Inheritance In Python
- Best Practices for Implementing Inheritance in Python
- Avoiding Common Pitfalls in Python Inheritance
- Conclusion
- Frequently Asked Questions
- 💡 Python Inheritance Quiz – Are You Ready?
- What Is The Python List append() Method?
- Adding Elements To A Python List Using append()
- Populate A Python List Using append()
- Adding Different Data Types To Python List Using append()
- Adding A List To Python List Using append()
- Nested Lists With Python List append() Method
- Practical Use Cases Of Python List append() Method
- How append() Method Affects List Performance
- Avoiding Common Mistakes When Using Python List append()
- Comparing extend() With append() Python List Method
- Conclusion
- Frequently Asked Questions
- 🧠 Think You Know Python List append()? Take A Quiz!
- What Is A Linked List In Python?
- Types Of Linked Lists In Python
- How To Create A Linked List In Python
- How To Traverse A Linked List In Python & Retrieve Elements
- Inserting Elements In A Linked List In Python
- Deleting Elements From A Linked List In Python
- Update A Node Of Linked List In Python
- Reversing A Linked List In Python
- Calculating Length Of A Linked List In Python
- Comparing Arrays And Linked Lists In Python
- Advantages & Disadvantages Of Linked List In Python
- When To Use Linked Lists Over Other Data Structures
- Practical Applications Of Linked Lists In Python
- Conclusion
- Frequently Asked Questions
- 🔗 Linked List Logic: Can You Ace This Quiz?
- What Is Extend In Python?
- Extend In Python With List
- Extend In Python With String
- Extend In Python With Tuple
- Extend In Python With Set
- Extend In Python With Dictionary
- Other Methods To Extend A List In Python
- Difference Between append() and extend() In Python
- Conclusion
- Frequently Asked Questions
- Think You Know extend() In Python? Prove It!
- What Is Recursion In Python?
- Key Components Of Recursive Functions In Python
- Implementing Recursion In Python
- Recursion Vs. Iteration In Python
- Tail Recursion In Python
- Infinite Recursion In Python
- Advantages Of Recursion In Python
- Disadvantages Of Recursion In Python
- Best Practices For Using Recursion In Python
- Conclusion
- Frequently Asked Questions
- Recursive Thinking In Python: Test Your Skills!
- What Is Type Conversion In Python?
- Types Of Type Conversion In Python
- Implicit Type Conversion In Python
- Explicit Type Conversion In Python
- Functions Used For Explicit Data Type Conversion In Python
- Important Type Conversion Tips In Python
- Benefits Of Type Conversion In Python
- Conclusion
- Frequently Asked Questions
- Think You Know Type Conversion? Take A Quiz!
- What Is Scope In Python?
- Local Scope In Python
- Global Scope In Python
- Nonlocal (Enclosing) Scope In Python
- Built-In Scope In Python
- The LEGB Rule For Python Scope
- Python Scope And Variable Lifetime
- Best Practices For Managing Python Scope
- Conclusion
- Frequently Asked Questions
- Think You Know Python Scope? Test Yourself!
- Understanding The Continue Statement In Python
- How Does Continue Statement Work In Python?
- Python Continue Statement With For Loops
- Python Continue Statement With While Loops
- Python Continue Statement With Nested Loops
- Python Continue With If-Else Statement
- Difference Between Pass and Continue Statement In Python
- Practical Applications Of Continue Statement In Python
- Conclusion
- Frequently Asked Questions
- Python 'continue' Statement Quiz: Can You Ace It?
- What Are Control Statements In Python?
- Types Of Control Statements In Python
- Conditional Control Statements In Python
- Loop Control Statements In Python
- Control Flow Altering Statements In Python
- Exception Handling Control Statements In Python
- Conclusion
- Frequently Asked Questions
- Mastering Control Statements In Python – Take the Quiz!
- Difference Between Mutable And Immutable Data Types in Python
- What Is Mutable Data Type In Python?
- Types Of Mutable Data Types In Python
- What Are Immutable Data Types In Python?
- Types Of Immutable Data Types In Python
- Key Similarities Between Mutable And Immutable Data Types In Python
- When To Use Mutable Vs Immutable In Python?
- Conclusion
- Frequently Asked Questions
- Quiz Time: Mutable vs. Immutable In Python!
- What Is A List?
- What Is A Tuple?
- Difference Between List And Tuple In Python (Comparison Table)
- Syntax Difference Between List And Tuple In Python
- Mutability Difference Between List And Tuple In Python
- Other Difference Between List And Tuple In Python
- List Vs. Tuple In Python | Methods
- When To Use Tuples Over Lists?
- Key Similarities Between Tuples And Lists In Python
- Conclusion
- Frequently Asked Questions
- 🧐 Lists vs. Tuples Quiz: Test Your Python Knowledge!
- Introduction to Python
- Downloading & Installing Python, IDLE, Tkinter, NumPy & PyGame
- Creating A New Python Project
- How To Write Python Hello World Program In Python?
- Way To Write The Hello, World! Program In Python
- The Hello, World! Program In Python Using Class
- The Hello, World! Program In Python Using Function
- Print Hello World 5 Times Using A For Loop
- Conclusion
- Frequently Asked Questions
- 👋 Python's 'Hello, World!'—How Well Do You Know It?
- Algorithm Of Python Program To Add To Numbers
- Standard Program To Add Two Numbers In Python
- Python Program To Add Two Numbers With User-defined Input
- The add() Method In Python Program To Add Two Numbers
- Python Program To Add Two Numbers Using Lambda
- Python Program To Add Two Numbers Using Function
- Python Program To Add Two Numbers Using Recursion
- Python Program To Add Two Numbers Using Class
- How To Add Multiple Numbers In Python?
- Add Multiple Numbers In Python With User Input
- Time Complexities Of Python Programs To Add Two Numbers
- Conclusion
- Frequently Asked Questions
- 💡 Quiz Time: Python Addition Basics!
- Swapping in Python
- Swapping Two Variables Using A Temporary Variable
- Swapping Two Variables Using The Comma Operator In Python
- Swapping Two Variables Using The Arithmetic Operators (+,-)
- Swapping Two Variables Using The Arithmetic Operators (*,/)
- Swapping Two Variables Using The XOR(^) Operator
- Swapping Two Variables Using Bitwise Addition and Subtraction
- Swap Variables In A List
- Conclusion
- Frequently Asked Questions (FAQs)
- Quiz To Test Your Variable Swapping Knowledge
- What Is A Quadratic Equation? How To Solve It?
- How To Write A Python Program To Solve Quadratic Equations?
- Python Program To Solve Quadratic Equations Directly Using The Formula
- Python Program To Solve Quadratic Equations Using The Complex Math Module
- Python Program To Solve Quadratic Equations Using Functions
- Python Program To Solve Quadratic Equations & Find Number Of Solutions
- Python Program To Plot Quadratic Functions
- Conclusion
- Frequently Asked Questions
- Quadratic Equations In Python Quiz: Test Your Knowledge!
- What Is Decimal Number System?
- What Is Binary Number System?
- What Is Octal Number System?
- What Is Hexadecimal Number System?
- Python Program to Convert Decimal to Binary, Octal, And Hexadecimal Using Built-In Function
- Python Program To Convert Decimal To Binary Using Recursion
- Python Program To Convert Decimal To Octal Using Recursion
- Python Program To Convert Decimal To Hexadecimal Using Recursion
- Python Program To Convert Decimal To Binary Using While Loop
- Python Program To Convert Decimal To Octal Using While Loop
- Python Program To Convert Decimal To Hexadecimal Using While Loop
- Convert Decimal To Binary, Octal, And Hexadecimal Using String Formatting
- Python Program To Convert Binary, Octal, And Hexadecimal String To A Number
- Complexity Comparison Of Python Programs To Convert Decimal To Binary, Octal, And Hexadecimal
- Conclusion
- Frequently Asked Questions
- 💡 Decimal To Binary, Octal & Hex: Quiz Time!
- What Is A Square Root?
- Python Program To Find The Square Root Of A Number
- The pow() Function In Python Program To Find The Square Root Of Given Number
- Python Program To Find Square Root Using The sqrt() Function
- The cmath Module & Python Program To Find The Square Root Of A Number
- Python Program To Find Square Root Using The Exponent Operator (**)
- Python Program To Find Square Root With A User-Defined Function
- Python Program To Find Square Root Using A Class
- Python Program To Find Square Root Using Binary Search
- Python Program To Find Square Root Using NumPy Module
- Conclusion
- Frequently Asked Questions
- 🤓 Think You Know Square Roots In Python? Take A Quiz!
- Understanding the Logic Behind the Conversion of Kilometers to Miles
- Steps To Write Python Program To Convert Kilometers To Miles
- Python Program To Convert Kilometer To Miles Without Function
- Python Program To Convert Kilometer To Miles Using Function
- Python Program to Convert Kilometer To Miles Using Class
- Tips For Writing Python Program To Convert Kilometer To Miles
- Conclusion
- Frequently Asked Questions
- 🧐 Mastered Kilometer To Mile Conversion? Prove It!
- Why Build A Calculator Program In Python?
- Prerequisites To Writing A Calculator Program In Python
- Approach For Writing A Calculator Program In Python
- Simple Calculator Program In Python
- Calculator Program In Python Using Functions
- Creating GUI Calculator Program In Python Using Tkinter
- Conclusion
- Frequently Asked Questions
- 🧮 Calculator Program In Python Quiz!
- The Calendar Module In Python
- Prerequisites For Writing A Calendar Program In Python
- How To Write And Print A Calendar Program In Python
- Calendar Program In Python To Display A Month
- Calendar Program In Python To Display A Year
- Conclusion
- Frequently Asked Questions
- Calendar Program In Python – Quiz Time!
- What Is The Fibonacci Series?
- Pseudocode Code For Fibonacci Series Program In Python
- Generating Fibonacci Series In Python Using Naive Approach (While Loop)
- Fibonacci Series Program In Python Using The Direct Formula
- How To Generate Fibonacci Series In Python Using Recursion?
- Generating Fibonacci Series In Python With Dynamic Programming
- Fibonacci Series Program In Python Using For Loop
- Generating Fibonacci Series In Python Using If-Else Statement
- Generating Fibonacci Series In Python Using Arrays
- Generating Fibonacci Series In Python Using Cache
- Generating Fibonacci Series In Python Using Backtracking
- Fibonacci Series In Python Using Power Of Matix
- Complexity Analysis For Fibonacci Series Programs In Python
- Applications Of Fibonacci Series In Python & Programming
- Conclusion
- Frequently Asked Questions
- 🤔 Think You Know Fibonacci Series? Take A Quiz!
- Different Ways To Write Random Number Generator Python Programs
- Random Module To Write Random Number Generator Python Programs
- The Numpy Module To Write Random Number Generator Python Programs
- The Secrets Module To Write Random Number Generator Python Programs
- Understanding Randomness and Pseudo-Randomness In Python
- Common Issues and Solutions in Random Number Generation
- Applications of Random Number Generator Python
- Conclusion
- Frequently Asked Questions
- Think You Know Python's Random Module? Prove It!
- What Is A Factorial?
- Algorithm Of Program To Find Factorial Of A Number In Python
- Pseudocode For Factorial Program in Python
- Factorial Program In Python Using For Loop
- Factorial Program In Python Using Recursion
- Factorial Program In Python Using While Loop
- Factorial Program In Python Using If-Else Statement
- The math Module | Factorial Program In Python Using Built-In Factorial() Function
- Python Program to Find Factorial of a Number Using Ternary Operator(One Line Solution)
- Python Program For Factorial Using Prime Factorization Method
- NumPy Module | Factorial Program In Python Using numpy.prod() Function
- Complexity Analysis Of Factorial Programs In Python
- Conclusion
- Frequently Asked Questions
- Think You Know Factorials In Python? Take A Quiz!
- What Is Palindrome In Python?
- Check Palindrome In Python Using While Loop (Iterative Approach)
- Check Palindrome In Python Using For Loop And Character Matching
- Check Palindrome In Python Using The Reverse And Compare Method (Python Slicing)
- Check Palindrome In Python Using The In-built reversed() And join() Methods
- Check Palindrome In Python Using Recursion Method
- Check Palindrome In Python Using Flag
- Check Palindrome In Python Using One Extra Variable
- Check Palindrome In Python By Building Reverse, One Character At A Time
- Complexity Analysis For Palindrome Programs In Python
- Real-World Applications Of Palindrome In Python
- Conclusion
- Frequently Asked Questions
- Think You Know Palindromes? Take A Quiz!
- Best Python Books For Beginners
- Best Python Books For Intermediate Level
- Best Python Books For Experts
- Best Python Books To Learn Algorithms
- Audiobooks of Python
- Best Books To Learn Python And Code Like A Pro
- To Learn Python Libraries
- Books To Provide Extra Edge In Python
- Python Project Ideas - Reference
- Quiz To Rehash Your Knowledge Of Python Books!
- What Are Classes In Python?
- How To Create/Define Classes In Python?
- What Is An Object In Python?
- How To Create Objects In Python Classes?
- Modifying & Deleting Objects In Python Classes
- The __init__() Method In Python Classes
- The __str__() Method In Python Classes
- The Role Of self Parameter In Python Classes
- Different Methods In Classes In Python
- Instance Attributes vs. Class Attributes In Python Classes
- Object-Oriented Programming (OOP) Concepts In Python
- Practical Examples Of Classes & Objects In Python
- Why & When To Use Classes In Python Programs?
- Common Pitfalls Of Using Classes In Python Programs
- Conclusion
- Frequently Asked Questions
- What Is A String & How Python Handles It?
- Concatenation For String Manipulation In Python
- String Comparison In Python
- Slicing For String Manipulation in Python
- String Replacement Manipulation In Python
- Reversion String Manipulation In Python
- String Formatting In Python
- The Length Of A String In Python
- Conversion Of String In Python
- String Methods For String Manipulation In Python
- Conclusion
- Frequently Asked Questions
- How To Convert String To List In Python? (List Of Methods)
- Using split() To Convert A String To A List In Python
- Using list() To Convert A String To A List In Python
- Using List Comprehension To Convert A String To A List
- Using map() To Convert A String To A List In Python
- Using ast.literal_eval() To Convert A String To A List In Python
- Using Regular Expressions To Convert A String To A List
- Using JSON Parsing To Convert A String To A List In Python
- Using String Slicing To Convert A String To A List In Python
- Using enumerate() to Convert a String to a List In Python
- Handling Edge Cases When Converting A String To A List In Python
- Performance Comparison Of Ways To Convert String To List In Python
- Conclusion
- Frequently Asked Questions
- What Is A Python List?
- What Are Python List Functions? (Table)
- The list() Function In Python
- The append() Python List Function
- The copy() Python List Function
- The count() Python List Function
- The clear() And remove() Python List Functions
- The extend() Python List Function
- The index() Python List Function
- The insert() Python List Function
- The pop() Python List Function
- The reverse() Python List Function
- The sort() Python List Function
- The len() Python List Function
- Conclusion
- Frequently Asked Questions
- What Are Identifiers In Python?
- Rules For Naming Identifiers In Python
- Valid & Invalid Identifiers In Python
- How To Test Validity Of Identifiers In Python
- Best Practices For Using Identifiers In Python
- What Are Keywords In Python?
- Difference Between Keywords & Identifiers In Python
- Conclusion
- Frequently Asked Questions
- What Is Python’s split() String Function?
- How Does Python's split() String Method Work?
- Using Python's split() String Method With & Without maxsplit
- Parsing A String Using split() Function In Python
- Examples Of Using Python's split() String Method (10 Use Cases)
- Conclusion
- Frequently Asked Questions
- What Are Keywords In Python?
- List Of Python Keywords
- Types/Categories Of Python Keywords
- Control Flow Keywords In Python
- Function & Class Definition Keywords
- Exception Handling Keywords In Python
- Variable Scope/Handling Python Keywords
- Operator Keywords In Python (Logical & Membership)
- Module & Import Management Keywords
- Asynchronous Programming Keywords In Python
- Context Management Keywords In Python
- Boolean & Null Values In Python
- Pattern Matching/Soft Python Keywords
- Type Alias Definitions Keyword In Python
- Conclusion
- Frequently Asked Questions
- What Are Arguments In Python?
- Types Of Arguments In Python
- What Are Keyword Arguments In Python?
- Why Use Keyword Arguments In Python?
- Where To Use Keyword Arguments In Python
- Arbitrary Arguments Vs. Keyword Arguments
- Conclusion
- Frequently Asked Questions
- What Is Method Overriding In Python?
- Features/Rules Of Method Overriding In Python
- Implementation Of Method Overriding In Python With Examples
- Method Overriding In Python With Multiple Inheritance
- Method Overriding In Python With Multilevel Inheritance
- Method Overloading In Python
- Common Mistakes In Method Overriding In Python
- Conclusion
- Frequently Asked Questions
Fibonacci Series In Python & Nth Term | Generate & Print (+Codes)

The Fibonacci series is one of the most well-known sequences in mathematics. Named after the Italian mathematician Leonardo of Pisa, known as Fibonacci, this series appears in various natural phenomena. It also has numerous applications in computer science, financial markets, and algorithm development. In this article, we will explore what this series is and how to generate the Fibonacci series in Python programming using various techniques.
What Is The Fibonacci Series?
The Fibonacci series is a sequence of numbers in which each number is the sum of the two preceding ones, typically starting with 0 and 1(seed values). The series appears in many different areas of mathematics and science, often in contexts with growth patterns and natural formations. In mathematical terms, the Fibonacci series is defined by the following recurrence relation:
F(n)=F(n−1)+F(n−2)
with the initial conditions:
F(0)=0 (0th term)
F(1)=1 (1st term)
This means that to find any number in the Fibonacci series, you add the two previous numbers, i.e., the (n-1)th term and the (n-2)th term in the series. The series usually starts as 0,1,1,2,3,5,8,13,21,34,…
Practical Occurrences of the Fibonacci Series:
The Fibonacci sequence is not just a theoretical construct; it appears in various natural and practical contexts:
-
Botanical Patterns: Many plants exhibit Fibonacci numbers in the arrangement of leaves, seeds, and flowers. For example, the number of petals on a flower is often a Fibonacci number. Lilies have 3 petals, buttercups have 5, and daisies can have 34, 55, or even 89 petals.
-
Rabbit Population Growth: Fibonacci originally introduced the series in the context of a problem involving the growth of a rabbit population. Suppose a pair of rabbits can reproduce starting at one month old and continue to produce another pair every subsequent month. The population growth of rabbits can be modelled by the Fibonacci series: 0 pairs at month 0, 1 pair at month 1, 1 pair at month 2, 2 pairs at month 3, 3 pairs at month 4, 5 pairs at month 5, and so on.
Visual Representation Of The Fibonacci Series
One of the most visually appealing representations of the Fibonacci series is the Fibonacci spiral. This is created by drawing quarter-circle arcs inside squares with side lengths that are Fibonacci numbers. When these squares are placed adjacently, a spiral pattern emerges, which can often be seen in natural formations such as shells and hurricanes.
Pseudocode Code For Fibonacci Series Program In Python
Here's a pseudocode to compute the Fibonacci series in Python language:
# Function to compute the Fibonacci series
function fibonacci(n):
if n <= 1:
return n
else:
# Initialize variables for the first two Fibonacci numbers
a = 0
b = 1
# Iterate from 2 to n to compute subsequent Fibonacci numbers
for i from 2 to n:
# Compute the next Fibonacci number by summing the previous two numbers
c = a + b
# Update variables for the next iteration
a = b
b = c
return b
# Example
n = 10
print("Fibonacci series up to", n, "terms:")
for i from 0 to n-1:
print(fibonacci(i), end=" ")
The pseudocode for the Fibonacci series in Python outlines a function to compute the Fibonacci numbers up to a given limit n.
- It initializes variables for the first two Fibonacci numbers, a and b, and then iteratively computes subsequent Fibonacci numbers using a loop.
- Each Fibonacci number is the sum of the two preceding numbers. Finally, it returns the last computed Fibonacci number.
Generating Fibonacci Series In Python Using Naive Approach (While Loop)
The native approach to generating the Fibonacci series involves using a while loop to iteratively compute each term of the series. The while loop iteratively executes a block of code till the time the loop condition is true. This simplest method is straightforward and easy to understand, making it a good starting point for beginners.
Below is a simple Python program example that illustrates the use of this approach to generate a Fibonacci series and print the n-th term.
Code Example:
def fibonacci_series_and_nth_term(n):
"""Generate Fibonacci series up to n terms and compute the n-th Fibonacci number using a naive approach with a while loop."""
if n <= 0:
return [], 0
elif n == 1:
return [0], 0
# Initialize the first two terms
series = [0, 1]
a, b = 0, 1
nth_term = 0
count = 2 # Already have two terms
# Iterative computation using a while loop
while count < n:
next_term = a + b
series.append(next_term)
a, b = b, next_term
count += 1
nth_term = series[-1] + series[-2] if n > 2 else 1
return series, nth_term
# Example usage with n = 6
n = 6
fibonacci_series, nth_term = fibonacci_series_and_nth_term(n)
print(f"Fibonacci series up to {n} terms: {fibonacci_series}")
print(f"The {n}-th Fibonacci term: {nth_term}")
ZGVmIGZpYm9uYWNjaV9zZXJpZXNfYW5kX250aF90ZXJtKG4pOgogICAgIiIiR2VuZXJhdGUgRmlib25hY2NpIHNlcmllcyB1cCB0byBuIHRlcm1zIGFuZCBjb21wdXRlIHRoZSBuLXRoIEZpYm9uYWNjaSBudW1iZXIgdXNpbmcgYSBuYWl2ZSBhcHByb2FjaCB3aXRoIGEgd2hpbGUgbG9vcC4iIiIKICAgIGlmIG4gPD0gMDoKICAgICAgICByZXR1cm4gW10sIDAKICAgIGVsaWYgbiA9PSAxOgogICAgICAgIHJldHVybiBbMF0sIDAKICAgIAogICAgIyBJbml0aWFsaXplIHRoZSBmaXJzdCB0d28gdGVybXMKICAgIHNlcmllcyA9IFswLCAxXQogICAgYSwgYiA9IDAsIDEKICAgIG50aF90ZXJtID0gMAogICAgY291bnQgPSAyICMgQWxyZWFkeSBoYXZlIHR3byB0ZXJtcwogICAgCiAgICAjIEl0ZXJhdGl2ZSBjb21wdXRhdGlvbiB1c2luZyBhIHdoaWxlIGxvb3AKICAgIHdoaWxlIGNvdW50IDwgbjoKICAgICAgICBuZXh0X3Rlcm0gPSBhICsgYgogICAgICAgIHNlcmllcy5hcHBlbmQobmV4dF90ZXJtKQogICAgICAgIGEsIGIgPSBiLCBuZXh0X3Rlcm0KICAgICAgICBjb3VudCArPSAxCiAgICAgICAgbnRoX3Rlcm0gPSBzZXJpZXNbLTFdICsgc2VyaWVzWy0yXSBpZiBuID4gMiBlbHNlIDEKICAgIAogICAgcmV0dXJuIHNlcmllcywgbnRoX3Rlcm0KCiMgRXhhbXBsZSB1c2FnZSB3aXRoIG4gPSA2Cm4gPSA2CmZpYm9uYWNjaV9zZXJpZXMsIG50aF90ZXJtID0gZmlib25hY2NpX3Nlcmllc19hbmRfbnRoX3Rlcm0obikKcHJpbnQoZiJGaWJvbmFjY2kgc2VyaWVzIHVwIHRvIHtufSB0ZXJtczoge2ZpYm9uYWNjaV9zZXJpZXN9IikKcHJpbnQoZiJUaGUge259LXRoIEZpYm9uYWNjaSB0ZXJtOiB7bnRoX3Rlcm19Iik=
Output:
Fibonacci series up to 6 terms: [0, 1, 1, 2, 3, 5]
The 6-th Fibonacci term: 8
Explanation:
In the simple Python code example-
- We define the fibonacci_series_and_nth_term(n) function to generate the Fibonacci series up to n terms and compute the n-th Fibonacci number using a naive approach with a while loop.
- Inside the function, we first have a docstring to describe it. Then, we enter an if-elif statement where the if-condition checks whether n is less than equal to 0.
- If the condition n<=0 is true, then the if-block is executed, and an empty list is returned and 0.
- If the condition n<=0 is false, we move to the elif-condition to check if n is equal to 1, i.e., n==1.
- If this condition is true, elif-block is executed, returning a list containing only 0 and the number 0 as the nth Fibonacci number.
- If the condition n==0 is also false, we move to the next line of the function and initialize a list called series with 2 values, 0 and 1.
- Then we initialize variables a and b to 0 and 1, respectively, variable nth_term to 0, and a variable count to 2. At this point, we already have two terms in the series.
- We then enter a while loop to iteratively compute the next terms of the Fibonacci series. The loop condition checks if the variable count is less than n.
- If the loop condition is met, we calculate the value of the next_term variable (which represents the net term in the series) by adding variables a to b.
- After that, we use the append() function to next_term to the series list.
- Then, we update the values of variables a to b, b to the next term, and increment count by 1 before the next iteration.
- After the loop completes iterations, the list series will contain the Fibonacci series and we compute the n-th Fibonacci number.
- Then, we compute the nth_term variable, which represents the nth number of the series using a formula with an if-else condition. Here, if n is greater than 2, we calculate it as the sum of the last two terms in the series. Otherwise, it's 1.
- Finally, the function returns the series list and the n-th Fibonacci number.
- In the main part of the program, we initialize a variable n with the value 6. This represents the number of elements in the series.
- We then call the fibonacci_series_and_nth_term() function, passing n as an argument.
- The function calculates the Fibonacci series up to 6 terms, and the 6-th Fibonacci term and outcome are stored in variables fibonacci_series and nth_term, respectively.
- Lastly, we use a set of print() statements to display these values to the console.
Time Complexity: O(n)
Space Complexity: O(1)
Fibonacci Series Program In Python Using The Direct Formula
Binet's formula provides a direct mathematical expression to compute the n-th Fibonacci number without iterating through the series. We can leverage this formula to generate the nth terms of the Fibonacci series in Python. This approach offers a concise and efficient solution, particularly for large values of n, bypassing the need for iterative or recursive computation.
The Binet formula for finding the n-th Fibonacci number is as follows:

This direct formula computes the n-th Fibonacci number directly without requiring intermediate computations or storage, making it highly efficient and suitable for situations where high-performance calculation is essential. Below is a sample Python program that illustrates the use of this formula to generate the number of the Fibonacci series.
Code Example:
import math
def fibonacci_direct_formula(n):
"""Compute the nth Fibonacci number using a direct formula."""
phi = (1 + math.sqrt(5)) / 2
return round((phi ** n - (1 - phi) ** n) / math.sqrt(5))
# Example usage with n = 7
n = 7
nth_term = fibonacci_direct_formula(n)
print(f"The {n}-th Fibonacci number: {nth_term}")
aW1wb3J0IG1hdGgKCmRlZiBmaWJvbmFjY2lfZGlyZWN0X2Zvcm11bGEobik6CiAgICAiIiJDb21wdXRlIHRoZSBudGggRmlib25hY2NpIG51bWJlciB1c2luZyBhIGRpcmVjdCBmb3JtdWxhLiIiIgogICAgcGhpID0gKDEgKyBtYXRoLnNxcnQoNSkpIC8gMgogICAgcmV0dXJuIHJvdW5kKChwaGkgKiogbiAtICgxIC0gcGhpKSAqKiBuKSAvIG1hdGguc3FydCg1KSkKCiMgRXhhbXBsZSB1c2FnZSB3aXRoIG4gPSA3Cm4gPSA3Cm50aF90ZXJtID0gZmlib25hY2NpX2RpcmVjdF9mb3JtdWxhKG4pCnByaW50KGYiVGhlIHtufS10aCBGaWJvbmFjY2kgbnVtYmVyOiB7bnRoX3Rlcm19Iik=
Output:
The 7-th Fibonacci number: 13
Explanation:
In the sample Python code, we first import the math module.
- Then, we define the fibonacci_direct_formula(n) function to compute the n-th Fibonacci number using the direct formula, i.e., the Binet Formula.
- Inside the function, we first define a variable phi, i.e., the golden ratio as (1 + math.sqrt(5)) / 2. We use the sqrt() function from math module to calculate the square root of the 5.
- Next, we apply Binet's formula for Fibonacci numbers, which states that the n-th Fibonacci number can be computed using the expression (phi ** n - (1 - phi) ** n) / sqrt(5).
- The function returns the nearest integer to the value calculated by the formula, using the round() function and returns that as the n-th Fibonacci number.
- In the main part, we initialize a variable n with the value 7 and then call the fibonacci_direct_formula() function, passing n as an argument.
- The function calculates and returns the 7th term of the series, which is stored in the variable nth_term.
- Lastly, we use a print() function to display this value to the console along with a string message using f-strings.
Time Complexity: O(1)
Space Complexity: O(n)
How To Generate Fibonacci Series In Python Using Recursion?
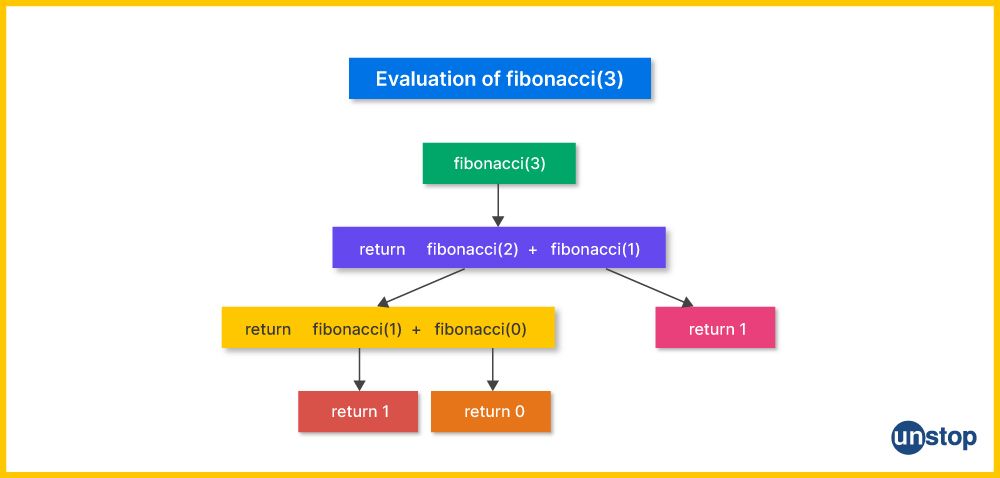
A recursive function is a special type of function that calls itself over and over again. We can write a Fibonacci series program in Python using recursion, where each Fibonacci number is computed by recursively calling the function itself with smaller input values until it reaches base cases. The recursive function definition method directly mirrors the mathematical definition of the Fibonacci sequence, making the code intuitive and easy to understand.
Look at the Python program sample below to understand how to define such a function to generate a Fibonacci series as well as the nth number.
Code Example:
def fibonacci_recursive(n):
"""Compute the nth Fibonacci number using recursion function."""
# Base cases
if n <= 1:
return n
# Recursively compute Fibonacci number
else:
return fibonacci_recursive(n - 1) + fibonacci_recursive(n - 2)
def fibonacci_series_recursive(n):
"""Generate Fibonacci series up to n terms using recursion."""
series = [fibonacci_recursive(i) for i in range(n)]
return series
# Example usage with n = 5
n = 5
fibonacci_series = fibonacci_series_recursive(n)
nth_term = fibonacci_recursive(n)
print(f"Fibonacci series up to {n} terms: {fibonacci_series}")
print(f"The {n}-th Fibonacci term: {nth_term}")
ZGVmIGZpYm9uYWNjaV9yZWN1cnNpdmUobik6CiAgICAiIiJDb21wdXRlIHRoZSBudGggRmlib25hY2NpIG51bWJlciB1c2luZyByZWN1cnNpb24gZnVuY3Rpb24uIiIiCiAgICAjIEJhc2UgY2FzZXMKICAgIGlmIG4gPD0gMToKICAgICAgICByZXR1cm4gbgogICAgIyBSZWN1cnNpdmVseSBjb21wdXRlIEZpYm9uYWNjaSBudW1iZXIKICAgIGVsc2U6CiAgICAgICAgcmV0dXJuIGZpYm9uYWNjaV9yZWN1cnNpdmUobiAtIDEpICsgZmlib25hY2NpX3JlY3Vyc2l2ZShuIC0gMikKCmRlZiBmaWJvbmFjY2lfc2VyaWVzX3JlY3Vyc2l2ZShuKToKICAgICIiIkdlbmVyYXRlIEZpYm9uYWNjaSBzZXJpZXMgdXAgdG8gbiB0ZXJtcyB1c2luZyByZWN1cnNpb24uIiIiCiAgICBzZXJpZXMgPSBbZmlib25hY2NpX3JlY3Vyc2l2ZShpKSBmb3IgaSBpbiByYW5nZShuKV0KICAgIHJldHVybiBzZXJpZXMKCiMgRXhhbXBsZSB1c2FnZSB3aXRoIG4gPSA1Cm4gPSA1CmZpYm9uYWNjaV9zZXJpZXMgPSBmaWJvbmFjY2lfc2VyaWVzX3JlY3Vyc2l2ZShuKQpudGhfdGVybSA9IGZpYm9uYWNjaV9yZWN1cnNpdmUobikKcHJpbnQoZiJGaWJvbmFjY2kgc2VyaWVzIHVwIHRvIHtufSB0ZXJtczoge2ZpYm9uYWNjaV9zZXJpZXN9IikKcHJpbnQoZiJUaGUge259LXRoIEZpYm9uYWNjaSB0ZXJtOiB7bnRoX3Rlcm19Iik=
Output:
Fibonacci series up to 5 terms: [0, 1, 1, 2, 3]
The 5-th Fibonacci term: 5
Explanation:
In the Python code sample-
- We define the function fibonacci_recursive(n), which takes an integer parameter n and computes the n-th Fibonacci number using recursion.
- In this function, we define the base case using the if-else statement. The statement condition states that if n is less than or equal to 1, i.e., n<=1 is true, we return n directly.
- If the condition is false, i.e., for values of n greater than 1, we recursively call fibonacci_recursive(n - 1) and fibonacci_recursive(n - 2) to compute the (n - 1)-th and (n - 2)-th Fibonacci numbers, respectively.
- The function then returns the sum of these two values to obtain the n-th Fibonacci number.
- Next, we define another function fibonacci_series_recursive(n), which also takes variable n as a parameter and generates the Fibonacci series up to n terms using recursion.
- Inside this function, we use list comprehension to generate a list called series by calling fibonacci_recursive(i) for each index i from 0 to n - 1.
- This will generate every Fibonacci number at the ith position till n and return the series.
- In the main part, we initialize a variable n to the value 5 and call the fibonacci_series_recursive() function, passing n as an argument.
- The invoked function generates the Fibonacci series up to 5 terms, and the outcome is stored in the variable fibonacci_series.
- Next, we call the fibonacci_recursive() function by passing n as an argument. The function output here is the 5th Fibonacci number which is stored in the nth_term variable.
- Lastly, we use a set of print() functions with f-strings to display both these values to the console.
Time Complexity: O(n)
Space Complexity: O(n)
Generating Fibonacci Series In Python With Dynamic Programming
Dynamic programming is a method used to solve problems by breaking them down into simpler subproblems and storing the results of these subproblems to avoid redundant calculations. We can generate the Fibonacci series in Python using dynamic programming by iteratively building the sequence from the bottom up.
The dynamic programming approach for generating the Fibonacci series involves creating an array to store Fibonacci numbers as they are computed. This method avoids the exponential time complexity of the naive recursive approach by using an iterative process and maintaining a table of already computed Fibonacci values. The example Python program below illustrates the use of this approach to generate the Fibonacci series in Python and the nth term.
Code Example:
def fibonacci_dynamic(n):
"""Calculate the n-th Fibonacci number using dynamic programming."""
if n <= 0:
return 0
elif n == 1:
return 1
fib = [0] * (n + 1)
fib[1] = 1
for i in range(2, n + 1):
fib[i] = fib[i - 1] + fib[i - 2]
return fib[n]
def fibonacci_series_dynamic(n):
"""Generate Fibonacci series up to n terms using dynamic programming."""
if n <= 0:
return []
elif n == 1:
return [0]
fib = [0] * n
fib[1] = 1
for i in range(2, n):
fib[i] = fib[i - 1] + fib[i - 2]
return fib
# Example usage
n_values = [15]
for n in n_values:
print(f"Fibonacci series up to {n} terms (Dynamic Programming): {fibonacci_series_dynamic(n)}")
print(f"The {n}-th Fibonacci number (Dynamic Programming): {fibonacci_dynamic(n)}")
print()
ZGVmIGZpYm9uYWNjaV9keW5hbWljKG4pOgogICAgIiIiQ2FsY3VsYXRlIHRoZSBuLXRoIEZpYm9uYWNjaSBudW1iZXIgdXNpbmcgZHluYW1pYyBwcm9ncmFtbWluZy4iIiIKICAgIGlmIG4gPD0gMDoKICAgICAgICByZXR1cm4gMAogICAgZWxpZiBuID09IDE6CiAgICAgICAgcmV0dXJuIDEKICAgIAogICAgZmliID0gWzBdICogKG4gKyAxKQogICAgZmliWzFdID0gMQogICAgCiAgICBmb3IgaSBpbiByYW5nZSgyLCBuICsgMSk6CiAgICAgICAgZmliW2ldID0gZmliW2kgLSAxXSArIGZpYltpIC0gMl0KICAgIAogICAgcmV0dXJuIGZpYltuXQoKZGVmIGZpYm9uYWNjaV9zZXJpZXNfZHluYW1pYyhuKToKICAgICIiIkdlbmVyYXRlIEZpYm9uYWNjaSBzZXJpZXMgdXAgdG8gbiB0ZXJtcyB1c2luZyBkeW5hbWljIHByb2dyYW1taW5nLiIiIgogICAgaWYgbiA8PSAwOgogICAgICAgIHJldHVybiBbXQogICAgZWxpZiBuID09IDE6CiAgICAgICAgcmV0dXJuIFswXQogICAgCiAgICBmaWIgPSBbMF0gKiBuCiAgICBmaWJbMV0gPSAxCiAgICAKICAgIGZvciBpIGluIHJhbmdlKDIsIG4pOgogICAgICAgIGZpYltpXSA9IGZpYltpIC0gMV0gKyBmaWJbaSAtIDJdCiAgICAKICAgIHJldHVybiBmaWIKCiMgRXhhbXBsZSB1c2FnZQpuX3ZhbHVlcyA9IFsxNV0KCmZvciBuIGluIG5fdmFsdWVzOgogICAgcHJpbnQoZiJGaWJvbmFjY2kgc2VyaWVzIHVwIHRvIHtufSB0ZXJtcyAoRHluYW1pYyBQcm9ncmFtbWluZyk6IHtmaWJvbmFjY2lfc2VyaWVzX2R5bmFtaWMobil9IikKcHJpbnQoZiJUaGUge259LXRoIEZpYm9uYWNjaSBudW1iZXIgKER5bmFtaWMgUHJvZ3JhbW1pbmcpOiB7Zmlib25hY2NpX2R5bmFtaWMobil9IikKcHJpbnQoKQ==
Output:
Fibonacci series up to 15 terms (Dynamic Programming): [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]
The 15-th Fibonacci number (Dynamic Programming): 610
Explanation:
In the example Python code-
- We define the function fibonacci_dynamic(n) to calculate the n-th Fibonacci number using dynamic programming.
- Inside the function, we use an if-elif statement, which first checks if the value of n is less than or equal to 0. If the condition n<=0 is true, we return 0 as the base case.
- If the elif condition n==1 is true, we return 1 as the second base case.
- If none of the conditions are true, we move to the next line in the function.
- Here, we create a list called fib of size n + 1 and initialize it with zeros.
- Next, we initialize the element at the 1st position, i.e., fib[1] to 1, to establish the base case for the dynamic programming approach.
- We then use a for loop to fill in the fib list from index 2 to n+1. For each index i, the element fib[i] is calculated by adding elements fib[i - 1] and fib[i - 2].
- After the loop completes iterations, the function returns fib[n], which is the n-th Fibonacci number.
- Next, we define another function, fibonacci_series_dynamic(n), to generate the Fibonacci series up to n terms using dynamic programming.
- Inside this function, we again use an if-elif statement to check base cases n<=0 and n==1. If n<=0 is true, the function returns an empty list.
- If the condition n==1 is true, then the function returns a list containing only 0. If none of the conditions are true, we move to the next line in the function.
- Here, we create a list fib of size n, initialize all its elements with zeros and then set the element fib[1] to 1 to establish the base case for the dynamic programming approach.
- Then, we use a for loop to fill in the fib list from index 2 to n - 1. For each index i, we calculate the element fib[i] by adding the elements fib[i - 1] and fib[i - 2].
- After the loop terminates, the list fib contains the Fibonacci series which is returned by the function.
- In the main section, we initialize a variable n_values to [15].
- After that, we use a for loop to iterate over each nth element in n_values.
- Inside the loop, we use a print() function to print the Fibonacci series up to n terms by calling the fibonacci_series_dynamic() function.
- We then call the fibonacci_dynamic() function inside a print() statement to print the n-th Fibonacci number.
Time Complexity: O(n)
Space Complexity: O(n)
Fibonacci Series Program In Python Using For Loop
A for loop is generally used to iteratively execute a block of code for a certain range. We can use this loop construct to generate a Fibonacci series in Python. This approach includes initializing the first two terms of the series, typically 0 and 1. Then, iteratively compute each subsequent term by adding the last two terms.
- The process continues for a specified number of iterations, typically up to a given number of terms.
- Within the loop, the next term is calculated by summing the last two terms, and this term is appended to a list or printed directly.
This iterative approach efficiently produces the Fibonacci series in Python without the need for recursion, making it suitable for generating the series up to a desired number of terms. The Python program example below illustrates this approach.
Code Example:
def fibonacci_series_for_loop(n):
"""Generate Fibonacci series up to n terms using a for loop."""
if n <= 0:
return []
elif n == 1:
return [0]
# Initialize the first two terms
series = [0, 1]
# Iterative computation using a for loop
for i in range(2, n):
next_term = series[-1] + series[-2]
series.append(next_term)
return series
# Example usage with n = 6
n = 6
fibonacci_series = fibonacci_series_for_loop(n)
print(f"Fibonacci series up to {n} terms: {fibonacci_series}")
ZGVmIGZpYm9uYWNjaV9zZXJpZXNfZm9yX2xvb3Aobik6CiAgICAiIiJHZW5lcmF0ZSBGaWJvbmFjY2kgc2VyaWVzIHVwIHRvIG4gdGVybXMgdXNpbmcgYSBmb3IgbG9vcC4iIiIKICAgIGlmIG4gPD0gMDoKICAgICAgICByZXR1cm4gW10KICAgIGVsaWYgbiA9PSAxOgogICAgICAgIHJldHVybiBbMF0KICAgIAogICAgIyBJbml0aWFsaXplIHRoZSBmaXJzdCB0d28gdGVybXMKICAgIHNlcmllcyA9IFswLCAxXQogICAgCiAgICAjIEl0ZXJhdGl2ZSBjb21wdXRhdGlvbiB1c2luZyBhIGZvciBsb29wCiAgICBmb3IgaSBpbiByYW5nZSgyLCBuKToKICAgICAgICBuZXh0X3Rlcm0gPSBzZXJpZXNbLTFdICsgc2VyaWVzWy0yXQogICAgICAgIHNlcmllcy5hcHBlbmQobmV4dF90ZXJtKQogICAgCiAgICByZXR1cm4gc2VyaWVzCgojIEV4YW1wbGUgdXNhZ2Ugd2l0aCBuID0gNgpuID0gNgpmaWJvbmFjY2lfc2VyaWVzID0gZmlib25hY2NpX3Nlcmllc19mb3JfbG9vcChuKQpwcmludChmIkZpYm9uYWNjaSBzZXJpZXMgdXAgdG8ge259IHRlcm1zOiB7Zmlib25hY2NpX3Nlcmllc30iKQ==
Output:
Fibonacci series up to 6 terms: [0, 1, 1, 2, 3, 5]
Explanation:
In the Python code example-
- We define the function fibonacci_series_for_loop(n) to generate the Fibonacci series up to n terms using a for loop.
- Inside the function, we first have an if-elif statement that checks conditions n<=0 and n==1.
- If the condition n<=0 is true, the function returns an empty list.
- If the condition n==1 is true, the function returns a list containing only 0.
- If none of the conditions are true, we move to the next line of the function.
- Here, we initialize a list called series with the first two Fibonacci numbers: [0, 1].
- Then, we use a for loop to iteratively compute the next terms of the Fibonacci series and add them to the list series. Inside the loop-
- We begin from index 2, and in every iteration, calculate the next_term by taking the sum of the last two terms in the series.
- Then, we use the append() function to add the element to the series list.
- Once the loop finishes iterations, the list variable series will contain the Fibonacci series up to n terms.
- In the main part of the program, we initialize a variable n with the value 6 and then call the fibonacci_series_for_loop() function by passing n as an argument.
- The function invoked calculates and returns the Fibonacci series up to 6 terms and stores it in variable fibonacci_series.
- Finally, we use a print() statement to display the Fibonacci series.
Time Complexity: O(n)
Space Complexity: O(1)
Generating Fibonacci Series In Python Using If-Else Statement
The if-else statement allows you to implement two alternative blocks of code depending on the condition being met. You can use this conditional statement to generate the Fibonacci series in Python.
- Here, you must first initialize the first two terms of the sequence, conventionally 0 and 1.
- Then, iteratively compute each subsequent term by adding the previous two terms.
- The if-else statement is utilized to handle special cases, like when the desired number of terms (n) is less than or equal to 0, 1, or 2, where the Fibonacci series follows specific patterns.
- For larger values of n, the series is generated within a loop where each term is calculated based on the last two terms.
This approach offers a straightforward implementation, ensuring the correct sequence is generated while maintaining clarity in the code. The example program below illustrates how to generate and print the Fibonacci series in Python language.
Code Example:
def fibonacci_series_if_else(n):
"""Generate Fibonacci series up to n terms using if-else statements."""
series = []
if n <= 0:
return series
# Initialize the first two terms
series.append(0)
if n == 1:
return series
series.append(1)
if n == 2:
return series
# Iterative computation
for i in range(2, n):
next_term = series[-1] + series[-2]
series.append(next_term)
return series
# Example usage with n = 7
n = 7
fibonacci_series = fibonacci_series_if_else(n)
print(f"Fibonacci series up to {n} terms: {fibonacci_series}")
ZGVmIGZpYm9uYWNjaV9zZXJpZXNfaWZfZWxzZShuKToKICAgICIiIkdlbmVyYXRlIEZpYm9uYWNjaSBzZXJpZXMgdXAgdG8gbiB0ZXJtcyB1c2luZyBpZi1lbHNlIHN0YXRlbWVudHMuIiIiCiAgICBzZXJpZXMgPSBbXQogICAgaWYgbiA8PSAwOgogICAgICAgIHJldHVybiBzZXJpZXMKICAgIAogICAgIyBJbml0aWFsaXplIHRoZSBmaXJzdCB0d28gdGVybXMKICAgIHNlcmllcy5hcHBlbmQoMCkKICAgIGlmIG4gPT0gMToKICAgICAgICByZXR1cm4gc2VyaWVzCiAgICAKICAgIHNlcmllcy5hcHBlbmQoMSkKICAgIGlmIG4gPT0gMjoKICAgICAgICByZXR1cm4gc2VyaWVzCiAgICAKICAgICMgSXRlcmF0aXZlIGNvbXB1dGF0aW9uCiAgICBmb3IgaSBpbiByYW5nZSgyLCBuKToKICAgICAgICBuZXh0X3Rlcm0gPSBzZXJpZXNbLTFdICsgc2VyaWVzWy0yXQogICAgICAgIHNlcmllcy5hcHBlbmQobmV4dF90ZXJtKQogICAgCiAgICByZXR1cm4gc2VyaWVzCgojIEV4YW1wbGUgdXNhZ2Ugd2l0aCBuID0gNwpuID0gNwpmaWJvbmFjY2lfc2VyaWVzID0gZmlib25hY2NpX3Nlcmllc19pZl9lbHNlKG4pCnByaW50KGYiRmlib25hY2NpIHNlcmllcyB1cCB0byB7bn0gdGVybXM6IHtmaWJvbmFjY2lfc2VyaWVzfSIp
Output:
Fibonacci series up to 7 terms: [0, 1, 1, 2, 3, 5, 8]
Explanation:
In the example code-
- We define the function fibonacci_series_if_else(n) to generate the Fibonacci series up to n terms using if-else statements.
- Inside the function, we first initialize an empty list called series to store the Fibonacci series.
- Then, we have an if-statement, which checks if the value of n is less than or equal to 0. If the condition n<=0 is true, the function returns an empty list as there are no terms to generate.
- We then append the first term, 0, to the series using the append() function.
- The next if-statment checks whether the value of n equals 1. If the condition n==1 is true, the function returns the series containing only the first term.
- Once again, we use the append() function to add the second term (i.e., 1) to the list series.
- Another if-statement checks where the value of n equals 2. If the condition n==2 is true, the function returns the series containing the first two terms.
- If none of the if-conditions are met, we move to a for loop that iteratively computes the terms of the Fibonacci series starting from the index position 2.
- The loop iterates till the loop control variable i becomes equal to n.
- In every iteration, the next term of the series, represented by variable next_term, is calculated by adding the previous terms.
- The next_term is then appended to the list series using the append() function.
- Once the loop finishes iterations, the list series holds the Fibonacci series up to n terms.
- In the main section, we initialize a variable n with the value 7 and call the fibonacci_series_if_else() function.
- The function computes the Fibonacci series up to 7 terms and stores it in the variable fibonacci_series, which we print to the console using the print() function.
Time Complexity: O(n)
Space Complexity: O(1)
Note that the else part of the statement, while not written, is implicit in the structure of the Python code.
Generating Fibonacci Series In Python Using Arrays
When generating and printing a Fibonacci series in Python using arrays, you must first initialize an array to store the series. Then, iteratively compute each subsequent term using array operations.
- Typically, the first two terms of the series, 0 and 1, are initialized in the array.
- Subsequent terms are calculated by adding the last two terms in the array.
- This process continues until the desired number of terms is generated.
- The resulting array contains the Fibonacci series up to the specified length.
- Additionally, to compute the n-th Fibonacci number, the last element of the generated array is returned.
The example below illustrates this approach to provide you with a better understanding of the concept.
Code Example:
def fibonacci_array(n):
"""Generate Fibonacci series up to n terms using arrays."""
if n <= 0:
return []
elif n == 1:
return [0]
elif n == 2:
return [0, 1]
# Initialize array with the first two terms
series = [0, 1]
# Iteratively compute subsequent terms
for i in range(2, n):
next_term = series[i - 1] + series[i - 2]
series.append(next_term)
return series
def nth_fibonacci_array(n):
"""Compute the nth Fibonacci number using arrays."""
series = fibonacci_array(n)
return series[-1] if series else None
# Example usage with n = 2
n = 2
fibonacci_series = fibonacci_array(n)
nth_term = nth_fibonacci_array(n)
print(f"Fibonacci series up to {n} terms: {fibonacci_series}")
print(f"The {n}-th Fibonacci term: {nth_term}")
ZGVmIGZpYm9uYWNjaV9hcnJheShuKToKICAgICIiIkdlbmVyYXRlIEZpYm9uYWNjaSBzZXJpZXMgdXAgdG8gbiB0ZXJtcyB1c2luZyBhcnJheXMuIiIiCiAgICBpZiBuIDw9IDA6CiAgICAgICAgcmV0dXJuIFtdCiAgICBlbGlmIG4gPT0gMToKICAgICAgICByZXR1cm4gWzBdCiAgICBlbGlmIG4gPT0gMjoKICAgICAgICByZXR1cm4gWzAsIDFdCiAgICAKICAgICMgSW5pdGlhbGl6ZSBhcnJheSB3aXRoIHRoZSBmaXJzdCB0d28gdGVybXMKICAgIHNlcmllcyA9IFswLCAxXQogICAgCiAgICAjIEl0ZXJhdGl2ZWx5IGNvbXB1dGUgc3Vic2VxdWVudCB0ZXJtcwogICAgZm9yIGkgaW4gcmFuZ2UoMiwgbik6CiAgICAgICAgbmV4dF90ZXJtID0gc2VyaWVzW2kgLSAxXSArIHNlcmllc1tpIC0gMl0KICAgICAgICBzZXJpZXMuYXBwZW5kKG5leHRfdGVybSkKICAgIAogICAgcmV0dXJuIHNlcmllcwoKZGVmIG50aF9maWJvbmFjY2lfYXJyYXkobik6CiAgICAiIiJDb21wdXRlIHRoZSBudGggRmlib25hY2NpIG51bWJlciB1c2luZyBhcnJheXMuIiIiCiAgICBzZXJpZXMgPSBmaWJvbmFjY2lfYXJyYXkobikKICAgIHJldHVybiBzZXJpZXNbLTFdIGlmIHNlcmllcyBlbHNlIE5vbmUKCiMgRXhhbXBsZSB1c2FnZSB3aXRoIG4gPSAyCm4gPSAyCmZpYm9uYWNjaV9zZXJpZXMgPSBmaWJvbmFjY2lfYXJyYXkobikKbnRoX3Rlcm0gPSBudGhfZmlib25hY2NpX2FycmF5KG4pCnByaW50KGYiRmlib25hY2NpIHNlcmllcyB1cCB0byB7bn0gdGVybXM6IHtmaWJvbmFjY2lfc2VyaWVzfSIpCnByaW50KGYiVGhlIHtufS10aCBGaWJvbmFjY2kgdGVybToge250aF90ZXJtfSIp
Output:
Fibonacci series up to 2 terms: [0, 1]
The 2-th Fibonacci term: 1
Explanation:
In the example-
- We first define the function fibonacci_array(n) to generate the Fibonacci series up to n terms using arrays.
- Inside the function, we have an if-elif-elif structure that checks conditions n<=0, n==1, and n==2.
- If condition n<=0 is true, the function returns an empty list.
- If condition n==1 is true, the function returns a list containing just [0].
- If condition n==2 is true, the function returns a list containing [0, 1].
- If none of the conditions are met, we move to the next line of the function.
- Then, we initialize an array named series with the first two terms [0, 1].
- Next, we use a for loop to iteratively compute the subsequent terms of the Fibonacci series from index 2 to n-1.
- In each iteration, we compute the next term as the sum of the last two terms in the series (series[i - 1] + series[i - 2]) and append it to the series using the append() function.
- After the loop completes execution, the array series contains the Fibonacci series up to n terms, which the function then returns.
- Next, we define another function function, nth_fibonacci_array(n), to compute the n-th Fibonacci number using arrays.
- Inside this function, we first call the fibonacci_array(n) to get the Fibonacci series up to n terms that is stored in the array series.
- Then, we calculate and return the last element of the series as the n-th Fibonacci number if the series is not empty. Otherwise, we return None.
- To demonstrate the usage of these functions, we initialize a variable n with 2 in the main segment.
- Then, we call the fibonacci_array(n) function, passing n as an argument. This function calculates the Fibonacci series and stores it in the variable fibonacci_series.
- After that, we call the nth_fibonacci_array() function to compute the 2nd Fibonacci number directly and store it in the nth_term variable.
- We print both the Fibonacci series and the 2nd Fibonacci number using print() function.
Time Complexity: O(n)
Space Complexity: O(n)
Generating Fibonacci Series In Python Using Cache
The caching approach to generating the Fibonacci series in Python optimizes computation by storing previously computed Fibonacci numbers in a cache, avoiding redundant calculations.
- It begins with initializing a cache to store Fibonacci numbers, typically starting with 0 and 1.
- Then, a recursive function computes Fibonacci numbers, utilizing the cache to retrieve previously computed values when available.
This method significantly improves efficiency, particularly for large Fibonacci numbers or series.
Code Example:
from functools import lru_cache
@lru_cache(maxsize=None)
def fibonacci_cache(n):
"""Compute the nth Fibonacci number using a cache (memoization)."""
if n <= 1:
return n
else:
return fibonacci_cache(n - 1) + fibonacci_cache(n - 2)
def fibonacci_series_cache(n):
"""Generate Fibonacci series up to n terms using a cache (memoization)."""
series = [fibonacci_cache(i) for i in range(n)]
return series
# Example usage with n = 4
n = 4
fibonacci_series = fibonacci_series_cache(n)
nth_term = fibonacci_cache(n)
print(f"Fibonacci series up to {n} terms: {fibonacci_series}")
print(f"The {n}-th Fibonacci term: {nth_term}")
ZnJvbSBmdW5jdG9vbHMgaW1wb3J0IGxydV9jYWNoZQoKQGxydV9jYWNoZShtYXhzaXplPU5vbmUpCmRlZiBmaWJvbmFjY2lfY2FjaGUobik6CiAgICAiIiJDb21wdXRlIHRoZSBudGggRmlib25hY2NpIG51bWJlciB1c2luZyBhIGNhY2hlIChtZW1vaXphdGlvbikuIiIiCiAgICBpZiBuIDw9IDE6CiAgICAgICAgcmV0dXJuIG4KICAgIGVsc2U6CiAgICAgICAgcmV0dXJuIGZpYm9uYWNjaV9jYWNoZShuIC0gMSkgKyBmaWJvbmFjY2lfY2FjaGUobiAtIDIpCgpkZWYgZmlib25hY2NpX3Nlcmllc19jYWNoZShuKToKICAgICIiIkdlbmVyYXRlIEZpYm9uYWNjaSBzZXJpZXMgdXAgdG8gbiB0ZXJtcyB1c2luZyBhIGNhY2hlIChtZW1vaXphdGlvbikuIiIiCiAgICBzZXJpZXMgPSBbZmlib25hY2NpX2NhY2hlKGkpIGZvciBpIGluIHJhbmdlKG4pXQogICAgcmV0dXJuIHNlcmllcwoKIyBFeGFtcGxlIHVzYWdlIHdpdGggbiA9IDQKbiA9IDQKZmlib25hY2NpX3NlcmllcyA9IGZpYm9uYWNjaV9zZXJpZXNfY2FjaGUobikKbnRoX3Rlcm0gPSBmaWJvbmFjY2lfY2FjaGUobikKcHJpbnQoZiJGaWJvbmFjY2kgc2VyaWVzIHVwIHRvIHtufSB0ZXJtczoge2ZpYm9uYWNjaV9zZXJpZXN9IikKcHJpbnQoZiJUaGUge259LXRoIEZpYm9uYWNjaSB0ZXJtOiB7bnRoX3Rlcm19Iik=
Output:
Fibonacci series up to 4 terms: [0, 1, 1, 2]
The 4-th Fibonacci term: 3
Explanation:
In the above code, we first import the lru_cache decorator from the functools module to enable caching (memoization).
- We define the function fibonacci_cache(n) to compute the n-th Fibonacci number using a cache. We decorate this function with @lru_cache(maxsize=None) to enable unlimited caching.
- Inside the function, an if-else statement checks if the value of n is less than or equal to 1. If the condition n<=1 is true, the function returns n (handling the base cases of 0 and 1).
- For other values of n, the function recursively calls the fibonacci_cache(n - 1) and fibonacci_cache(n - 2) functions, adding their results to compute the n-th Fibonacci number.
- Next, we define the function fibonacci_series_cache(n) to generate the Fibonacci series up to n terms using the cache.
- Here, we use list comprehension to generate the series by calling fibonacci_cache(i) for each index from 0 to n - 1.
- Then, the function returns the generated Fibonacci series, which is stored in the variable series.
- To demonstrate the usage, we initialize the variable n with value 4 and call the fibonacci_series_cache() function in the main part.
- The function computes the Fibonacci series up to 4 terms and stores it in the fibonacci_series variable.
- Next, we call the fibonacci_cache() function to compute the 4-th Fibonacci number which it stores in the nth_term variable.
- Finally, we print the Fibonacci series and the 4-th Fibonacci term using the print() function.
Time Complexity: O(n)
Space Complexity: O(n)
Generating Fibonacci Series In Python Using Backtracking
Generating the Fibonacci series in Python using backtracking involves recursively computing each Fibonacci number by exploring all possible paths in a tree-like structure until reaching the base cases.
This popular method employs a recursive function to compute each Fibonacci number, which recursively calls itself to compute the nth Fibonacci number by summing the n−1th and n−2th Fibonacci numbers. The basic Python program example below illustrates this approach.
Code Example:
def fibonacci_backtracking(n, computed={0: 0, 1: 1}):
"""Compute the nth Fibonacci number using a backtracking-like approach."""
# If the value has already been computed, return it
if n in computed:
return computed[n]
# Recursively compute the previous two Fibonacci numbers
fib_n_minus_1 = fibonacci_backtracking(n - 1, computed)
fib_n_minus_2 = fibonacci_backtracking(n - 2, computed)
# Store the result in the computed dictionary
computed[n] = fib_n_minus_1 + fib_n_minus_2
return computed[n]
def fibonacci_series_backtracking(n):
"""Generate Fibonacci series up to n terms using a backtracking-like approach."""
series = [fibonacci_backtracking(i) for i in range(n)]
return series
# Example usage with n = 5
n = 5
fibonacci_series = fibonacci_series_backtracking(n)
nth_term = fibonacci_backtracking(n)
print(f"Fibonacci series up to {n} terms: {fibonacci_series}")
print(f"The {n}-th Fibonacci term: {nth_term}")
ZGVmIGZpYm9uYWNjaV9iYWNrdHJhY2tpbmcobiwgY29tcHV0ZWQ9ezA6IDAsIDE6IDF9KToKICAiIiJDb21wdXRlIHRoZSBudGggRmlib25hY2NpIG51bWJlciB1c2luZyBhIGJhY2t0cmFja2luZy1saWtlIGFwcHJvYWNoLiIiIgogICMgSWYgdGhlIHZhbHVlIGhhcyBhbHJlYWR5IGJlZW4gY29tcHV0ZWQsIHJldHVybiBpdAogIGlmIG4gaW4gY29tcHV0ZWQ6CiAgICByZXR1cm4gY29tcHV0ZWRbbl0KCiAgIyBSZWN1cnNpdmVseSBjb21wdXRlIHRoZSBwcmV2aW91cyB0d28gRmlib25hY2NpIG51bWJlcnMKICBmaWJfbl9taW51c18xID0gZmlib25hY2NpX2JhY2t0cmFja2luZyhuIC0gMSwgY29tcHV0ZWQpCiAgZmliX25fbWludXNfMiA9IGZpYm9uYWNjaV9iYWNrdHJhY2tpbmcobiAtIDIsIGNvbXB1dGVkKQoKICAjIFN0b3JlIHRoZSByZXN1bHQgaW4gdGhlIGNvbXB1dGVkIGRpY3Rpb25hcnkKICBjb21wdXRlZFtuXSA9IGZpYl9uX21pbnVzXzEgKyBmaWJfbl9taW51c18yCgogIHJldHVybiBjb21wdXRlZFtuXQoKZGVmIGZpYm9uYWNjaV9zZXJpZXNfYmFja3RyYWNraW5nKG4pOgogICIiIkdlbmVyYXRlIEZpYm9uYWNjaSBzZXJpZXMgdXAgdG8gbiB0ZXJtcyB1c2luZyBhIGJhY2t0cmFja2luZy1saWtlIGFwcHJvYWNoLiIiIgogIHNlcmllcyA9IFtmaWJvbmFjY2lfYmFja3RyYWNraW5nKGkpIGZvciBpIGluIHJhbmdlKG4pXQogIHJldHVybiBzZXJpZXMKCiMgRXhhbXBsZSB1c2FnZSB3aXRoIG4gPSA1Cm4gPSA1CmZpYm9uYWNjaV9zZXJpZXMgPSBmaWJvbmFjY2lfc2VyaWVzX2JhY2t0cmFja2luZyhuKQpudGhfdGVybSA9IGZpYm9uYWNjaV9iYWNrdHJhY2tpbmcobikKcHJpbnQoZiJGaWJvbmFjY2kgc2VyaWVzIHVwIHRvIHtufSB0ZXJtczoge2ZpYm9uYWNjaV9zZXJpZXN9IikKcHJpbnQoZiJUaGUge259LXRoIEZpYm9uYWNjaSB0ZXJtOiB7bnRoX3Rlcm19Iik=
Output:
Fibonacci series up to 5 terms: [0, 1, 1, 2, 3]
The 5-th Fibonacci term: 5
Explanation:
In the code-
- We define the function fibonacci_backtracking() to compute the n-th Fibonacci number using a backtracking-like approach with memoization.
- The function takes a variable n and a dictionary computed, which is initialized with base cases: 0 maps to 0, and 1 maps to 1, as parameters.
- Inside the function, we have an if-else statement that checks if the n-th Fibonacci number is already computed by checking if n is in the computed dictionary. If the condition is true, the function returns the precomputed value.
- If the value is not precomputed, we recursively compute the previous two Fibonacci numbers by calling fibonacci_backtracking(n - 1, computed) and fibonacci_backtracking(n - 2, computed) functions.
- The outcomes of these functions are stored in the variables fib_n_minus_1 and fib_n_minus_1, respectively.
- Next, we store the sum of these two current values in the computed dictionary under the key n., which the function then returns as the computed n-th Fibonacci number.
- After that, we define another function, fibonacci_series_backtracking(n), to generate the Fibonacci series up to n terms using the backtracking-like approach.
- Inside the function, we declare a list called series and assign it a value using list comprehension to generate the series by calling fibonacci_backtracking(i) for each index from 0 to n - 1.
- The function returns this list containing the Fibonacci series.
- In the main part, we initialize a variable n with the value 5 and call the fibonacci_series_backtracking() function.
- This function computes the Fibonacci series up to 5 terms and stores it in fibonacci_series.
- Following this, we call the fibonacci_backtracking() function to compute the 5th Fibonacci number stored in the nth_term variable.
- Finally, we print the Fibonacci series and the 5th Fibonacci term using the print() function.
Time Complexity: O(2^n)
Space Complexity: O(2^n)
Fibonacci Series In Python Using Power Of Matix
The matrix exponentiation method for computing Fibonacci numbers leverages the properties of matrices to efficiently calculate the nth Fibonacci number. By representing the Fibonacci sequence as a matrix and using matrix exponentiation techniques, we can raise the Fibonacci matrix to the power of n to obtain the nth Fibonacci number directly.
Code Example:
import numpy as np
def fibonacci_matrix(n):
"""Compute the nth Fibonacci number using matrix exponentiation."""
if n == 0:
return 0
elif n == 1:
return 1
# Define Fibonacci matrix
fib_matrix = np.array([[1, 1], [1, 0]])
# Raise Fibonacci matrix to the power of (n-1)
result_matrix = np.linalg.matrix_power(fib_matrix, n-1)
# Extract Fibonacci number from resulting matrix
return result_matrix[0][0]
def fibonacci_series_matrix(n):
"""Generate Fibonacci series up to n terms using matrix exponentiation."""
series = [fibonacci_matrix(i) for i in range(n)]
return series
# Example usage with n = 7
n = 7
fibonacci_series = fibonacci_series_matrix(n)
nth_term = fibonacci_matrix(n)
print(f"Fibonacci series up to {n} terms: {fibonacci_series}")
print(f"The {n}-th Fibonacci term: {nth_term}")
aW1wb3J0IG51bXB5IGFzIG5wCgpkZWYgZmlib25hY2NpX21hdHJpeChuKToKICAiIiJDb21wdXRlIHRoZSBudGggRmlib25hY2NpIG51bWJlciB1c2luZyBtYXRyaXggZXhwb25lbnRpYXRpb24uIiIiCiAgaWYgbiA9PSAwOgogICAgcmV0dXJuIDAKICBlbGlmIG4gPT0gMToKICAgIHJldHVybiAxCgogICMgRGVmaW5lIEZpYm9uYWNjaSBtYXRyaXgKICBmaWJfbWF0cml4ID0gbnAuYXJyYXkoW1sxLCAxXSwgWzEsIDBdXSkKCiAgIyBSYWlzZSBGaWJvbmFjY2kgbWF0cml4IHRvIHRoZSBwb3dlciBvZiAobi0xKQogIHJlc3VsdF9tYXRyaXggPSBucC5saW5hbGcubWF0cml4X3Bvd2VyKGZpYl9tYXRyaXgsIG4tMSkKCiAgIyBFeHRyYWN0IEZpYm9uYWNjaSBudW1iZXIgZnJvbSByZXN1bHRpbmcgbWF0cml4CiAgcmV0dXJuIHJlc3VsdF9tYXRyaXhbMF1bMF0KCmRlZiBmaWJvbmFjY2lfc2VyaWVzX21hdHJpeChuKToKICAiIiJHZW5lcmF0ZSBGaWJvbmFjY2kgc2VyaWVzIHVwIHRvIG4gdGVybXMgdXNpbmcgbWF0cml4IGV4cG9uZW50aWF0aW9uLiIiIgogIHNlcmllcyA9IFtmaWJvbmFjY2lfbWF0cml4KGkpIGZvciBpIGluIHJhbmdlKG4pXQogIHJldHVybiBzZXJpZXMKCiMgRXhhbXBsZSB1c2FnZSB3aXRoIG4gPSA3Cm4gPSA3CmZpYm9uYWNjaV9zZXJpZXMgPSBmaWJvbmFjY2lfc2VyaWVzX21hdHJpeChuKQpudGhfdGVybSA9IGZpYm9uYWNjaV9tYXRyaXgobikKcHJpbnQoZiJGaWJvbmFjY2kgc2VyaWVzIHVwIHRvIHtufSB0ZXJtczoge2ZpYm9uYWNjaV9zZXJpZXN9IikKcHJpbnQoZiJUaGUge259LXRoIEZpYm9uYWNjaSB0ZXJtOiB7bnRoX3Rlcm19Iik=
Output:
Fibonacci series up to 7 terms: [0, 1, 1, 2, 3, 5, 8]
The 7-th Fibonacci term: 13
Explanation:
In the example, we begin by importing the NumPy module as np to use its functions.
- We define the function fibonacci_matrix(n) to compute the n-th Fibonacci number using matrix exponentiation.
- Inside the function, we use an if-else statement to handle the base cases with conditions n equals 0 and n equals 1.
- If condition n==0 is true, the function returns 0.
- If the condition n==1 is true, the function returns 1.
- Then, we define the Fibonacci matrix called fib_matrix as a NumPy array, i.e., [[1, 1], [1, 0]], using the array() function from the numpy module.
- Next, we raise the Fibonacci matrix to the power of (n - 1) using NumPy's np.linalg.matrix_power function, storing the resulting matrix in result_matrix.
- We extract the Fibonacci number from the resulting matrix. Specifically, the element in the first row and first column (result_matrix[0][0]) represents the n-th Fibonacci number that the function returns.
- After that, we define another function, fibonacci_series_matrix(n), to generate the Fibonacci series up to n terms using matrix exponentiation.
- Inside, we use list comprehension to generate the series by calling the fibonacci_matrix function for each index from 0 to n - 1.
- The outcome is stored in the list series, which the function returns.
- To demonstrate the usage of these functions, we initialize the variable n with value 7 and call the fibonacci_series_matrix() function.
- This invoked function computes the Fibonacci series up to 7 terms and stores it in fibonacci_series.
- Next, we call the fibonacci_matrix() function with n to compute the 7-th Fibonacci number stored in the nth_term variable.
- We print the Fibonacci series and the 7th Fibonacci term using the print() function.
Time Complexity: O( log n)
Space Complexity: O(log n)
Complexity Analysis For Fibonacci Series Programs In Python
The table below provides a comparison of the time and space complexities for each coding method to generate the Fibonacci series in Python, arranged in descending order.
| Method | Time Complexity | Space Complexity |
|---|---|---|
| Python Program for Fibonacci Series Using Power Of Matrix | O(logn) | O(logn) |
| Python Program for Fibonacci Series Using Dynamic Programming | O(n) | O(n) |
| Python Program for Fibonacci Series Using Cache | O(n) | O(n) |
| Python Program for Fibonacci Series Using Arrays | O(n) | O(n) |
| Python Program for Fibonacci Series Using Backtracking | O(2^n) | O(2^n) |
| Python Program for Fibonacci Series Using Recursion | O(2^n) | O(n) |
| Python Program for Fibonacci Series Using Direct Formula | O(1) | O(n) |
| Fibonacci Series In Python Using For Loop | O(n) | O(1) |
| Python Program for Fibonacci Series Using If-Else Statement | O(n) | O(1) |
| Python Program for Fibonacci Series Using Naive Approach(while loop) | O(n) | O(1) |
The methods are arranged based on time complexity, with the most efficient methods to generate the Fibonacci series in Python listed at the top.
Applications Of Fibonacci Series In Python & Programming
The Fibonacci series finds applications in various fields due to its mathematical properties and recurrence relation. Some notable applications include:
- Computer Science and Algorithms: Fibonacci numbers are used in algorithms related to dynamic programming, memoization, and optimization problems. They serve as a basis for developing efficient solutions to problems such as finding the shortest path in a graph, optimizing resource allocation, and generating permutations.
- Mathematics: Fibonacci numbers appear in various mathematical concepts, such as number theory, combinatorics, and geometry. They are closely related to the golden ratio, which has applications in art, architecture, and design.
- Finance and Economics: In finance, Fibonacci numbers and the golden ratio are applied in technical analysis to identify potential support and resistance levels in stock prices. Fibonacci retracement levels are commonly used by traders to predict market trends and make investment decisions. Additionally, Fibonacci sequences model population growth and the distribution of plants in botanical studies.
- Natural Sciences: Fibonacci numbers are observed in natural phenomena, including the arrangement of leaves on a stem, the spirals of sunflower seeds, the branching patterns of trees, and the structure of pinecones and pineapples. These patterns arise due to the optimization of space and resources during growth processes, leading to the prevalence of Fibonacci sequences in nature.
- Coding and Cryptography: Fibonacci numbers are used in coding theory and cryptography for error detection and correction, as well as in the generation of pseudorandom numbers. The mathematical properties of Fibonacci sequences contribute to the development of secure encryption algorithms and data transmission protocols.
- Artificial Intelligence and Machine Learning: Fibonacci numbers are incorporated into machine learning algorithms for pattern recognition, sequence prediction, and feature extraction. They provide a mathematical framework for modelling and analyzing complex data structures and time series data.
Conclusion
There are many ways to generate the Fibonacci series in Python, including recursion, iteration, dynamic programming, and matrix exponentiation. Python provides versatile tools for computing Fibonacci numbers. The ability to generate and print the Fibonacci series in Python (as well as the nth Fibonacci number) can have significant applications across diverse fields, including computer science, finance, natural sciences, cryptography, and artificial intelligence.
Its patterns and properties not only inspire algorithmic innovations but also shed light on the underlying mathematical principles governing complex systems in nature and society. Python's flexibility and simplicity make it an ideal platform for experimenting with Fibonacci sequences. By harnessing the power of Python, programmers and researchers can delve deeper into the mysteries of the Fibonacci series and unlock its potential to solve problems.
Frequently Asked Questions
Q. What is the Fibonacci series in Python, and how is it defined?
The Fibonacci series in Python is a sequence of numbers where each number is the sum of the two preceding ones, starting from 0 and 1. In mathematical terms, the Fibonacci series is defined recursively as:
F(0)=0
F(1)=1
F(n)=F(n−1)+F(n−2) for n≥2
In simpler terms, each Fibonacci number (except for the first two) is the sum of the two preceding Fibonacci numbers. This integer sequence starts with 0 and 1, and subsequent numbers are obtained by adding the previous two numbers. The Fibonacci series in Python is commonly used for various computational and mathematical purposes, such as algorithmic problem-solving, mathematical modelling, and generating sequences with interesting properties.
Q. What is the significance of the Fibonacci series in nature?
The Fibonacci series is observed in natural phenomena such as the arrangement of leaves on a stem, the spirals of sunflower seeds, the branching patterns of trees, and the structure of pinecones and pineapples. These patterns arise due to optimization principles in nature, making Fibonacci numbers a fundamental aspect of natural growth and organization.
Q. How can Python's built-in libraries, such as NumPy, be utilized to optimize Fibonacci sequence computations?
Python's built-in libraries, such as NumPy, can be leveraged to optimize Fibonacci sequence computations through matrix exponentiation. This basic idea exploits the fact that the nth Fibonacci number can be obtained by raising a specific Fibonacci matrix to the power of n and extracting the appropriate element from the resulting matrix.
Q. What are the applications of the Fibonacci series?
The Fibonacci series finds applications in various fields, including mathematics, computer science, finance, natural sciences, and cryptography. It is used in algorithms, technical analysis in stock trading, modelling natural phenomena, and generating pseudorandom numbers, among other applications.
Q. What are the advantages and disadvantages of using recursion to compute the Fibonacci series in Python?
Using recursion to compute the Fibonacci series in Python offers both advantages and disadvantages.
- The primary advantage is its simplicity and clarity; the recursive Fibonacci function directly mirrors the mathematical definition of the Fibonacci sequence, making the code easy to understand and write.
- This approach is particularly useful for educational purposes, as it clearly illustrates the concept of recursion and the base cases.
- However, the disadvantages are significant, especially for larger integer input values.
- Recursive computation of the Fibonacci series can be highly inefficient due to its exponential time complexity, O(2^n), resulting from redundant calculations of the same subproblems.
- Each Fibonacci number is recalculated multiple times, leading to excessive function calls and increased execution time.
- Additionally, deep recursion can cause a stack overflow, as Python has a limited recursion depth.
- These inefficiencies make the naive recursive solution impractical for large n.
- In such cases, iterative or dynamic programming methods are preferred for generating the Fibonacci series in Python.
🤔 Think You Know Fibonacci Series? Take A Quiz!
You might also be interested in reading the following:
- Convert Int To String In Python | Learn 6 Methods With Examples
- How To Print Without Newline In Python? (Mulitple Ways + Examples)
- How To Convert Python List To String? 8 Ways Explained (+Examples)
- Python Logical Operators, Short-Circuiting & More (With Examples)
- Python String.Replace() And 8 Other Ways Explained (+Examples)
- How To Reverse A String In Python? 10 Easy Ways With Examples
An economics graduate with a passion for storytelling, I thrive on crafting content that blends creativity with technical insight. At Unstop, I create in-depth, SEO-driven content that simplifies complex tech topics and covers a wide array of subjects, all designed to inform, engage, and inspire our readers. My goal is to empower others to truly #BeUnstoppable through content that resonates. When I’m not writing, you’ll find me immersed in art, food, or lost in a good book—constantly drawing inspiration from the world around me.
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter












Comments
Add comment