- Step 1: The Groundwork
- Step 2: The Three Sections
- Step 3: Practice Makes Improvement
- The Secret Ingredient
- Understanding Basics Of Number Series
- Types Of Number Series Reasoning Questions
- Addition & Multiplication In Number Series
- Square & Cube-Based Number Series Patterns
- Missing Terms & Arranging Sequences
- Tricks & Tips For Solving Number Series
- Selected Number Series Questions With Solutions
- Frequently Asked Questions (FAQs)
- Must Know Terminologies in Blood Relation Questions
- Basic Approaches to Solve Blood Relation Questions
- Types Of Blood Relation Questions
- Tips For Solving Blood Relation Questions
- Multiple Choice Questions (MCQs) with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Letter Series In Logical Reasoning
- Types Of Letter Series Patterns
- Tips For Solving Letter Series Reasoning
- Best Practice Question Samples With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basics of Problems On Age-Related Questions
- Formula to Solve Problems on Ages-Related Questions
- Types of Age-Related Questions & Examples
- Tips & Tricks for Solving Ages Problems
- Best MCQs on Problems on ages with solved answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition of Calendar
- Understanding Days of the Week
- What is a Leap Year?
- Concept of Odd Days in a Century
- Tips For Solving Calendar Reasoning Questions
- Best Calendar Reasoning Questions with Answers (MCQs)
- Frequently Asked Questions (FAQs)
- Basic Concepts of Clock
- Structure of a Clock
- Angle Equilavalence in Clock
- Tips For Solving Clock Questions
- Selected Clock Questions & Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding The Concept Of Direction Sense
- Tips For Effective Problem-Solving In Direction Sense
- Practical Test Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Dice Reasoning
- Dice Numbers In Dice Reasoning
- Classification Of Dice
- Constructed Vs Deconstructed Dice
- Tricks & Tips For Solving Dice Problems
- Practice MCQs With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Alphanumeric Series Defined
- Alphanumeric Series In Reasoning Tests
- Tips & Strategies For Solving Alphanumeric Series
- Practice Sample Questions With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept Of Mirror Image Reasoning Explained
- Important Terms In Mirror Image Reasoning
- Types Of Mirror Images
- Identifying Correct Mirror Image
- Finding Clock's Mirror Image
- Tips To Solve Mirror Images
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept & Overview Of Input-Output
- Input-Output In Competitive Exams
- Types Of Input-Output Problems
- Strategies, Tips & Tricks For Solving Reasoning Questions
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Finding The Odd One Out
- Tricks And Tips
- How to Find The Odd One Out?
- Solved MCQs with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Key Concepts
- Exploring Different Ranking Types
- Formula And Application Of Order And Ranking
- Tips For Solving Order & Ranking
- Selected Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Pipes & Cistern Aptitude
- Key Terminologies used in Pipes and Cisterns
- Pipes and Cisterns Formula with Examples
- Pipes and Cisterns Shortcut Tricks
- Tips For Solving Pipes & Cistern Problems
- Selected Questions & Answers For Practice (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Key Concept in Boats and Streams
- Formulas Of Boats & Streams
- Distance & Time Formula
- Tips For Solving Boats & Streams Questions
- Selected Practice Questions With Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept of Mixture and Alligation
- Types Of Alligation Questions
- Formula for Solving Mixture & Alligation
- Tips For Solving Mixture And Alligation
- Selected Questions With Answers For Practice
- Conclusion
- Frequently Asked Questions (FAQs)
- Concepts and Definitions Related to Time and Work
- Important Time And Work Formulas
- Tricks and Tips to Solve Time & Work Questions
- Time And Work MCQs with Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Harmonic Progression(HP)?
- Formula to find the nth Term in Harmonic Progression
- Formula to find the Sum of the nth Term in HP
- What is Harmonic Mean?
- Harmonic Progression Solved Best MCQs
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Mensuration in Maths?
- What are 2D figures in Mensuration?
- What are 3D figures in Mensuartion?
- Basic Terminologies In Mensuration
- Basic 2D Formulas in Mensuration
- Basic 3D Formulas in Mensuration
- 2D vs 3D in Mensuration
- Solved Questions With Solutions (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Relationship Between Time, Speed And Distance
- Conversion Units Time, Speed And Distance
- Average & Relative Speed: Two Trains Moving in the same or opposite direction
- Solved MCQs on Time, Speed And Distance
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Simplification in Maths?
- BODMAS Rule in Simplification Explained
- Simplification & Approximation Relation
- Key Terms in Simplification
- Examples Of Simplification Techniques
- Simplification Questions With Solved Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Height And Distance Important Terms
- Right Angled Triangle In Trigonometry
- Trigonometric Ratios
- Solved Examples For Better Understanding
- Height And Distance Applications In Trigonometry
- Height And Distance Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Interest Types
- Simple Interest Vs. Compound Interest
- Selected Solved Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basic Concepts Of Profit And Loss
- Determining Selling Price
- Calculating Discounts
- Formulas For Calculating Profit And Loss
- Examples Of Profit And Loss
- Profit & Loss Questions With Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Angle Of Elevation
- Key Terms Used In Angle Of Elevation
- Angle of Elevation Formula with Example
- Angle of Elevation vs. Angle of Depression
- Angle of Elevation MCQs with Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining HCF And LCM
- Calculation Methods Of HCF And LCM
- HCF By Prime Factorization Method
- LCM By Prime Factorization Method
- Difference Between HCF And LCM
- HCF & LCM Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- What is fraction and decimal?
- Understanding Decimal Fraction
- Place Value in Decimal Fraction
- Mathematical Operations with Decimal Fraction
- Practice with Solved Examples
- Summary
- Frequently Asked Questions
- All About Decimals
- All About Fractions
- How to Convert a Decimal into Fraction
- Simple vs Recurring Decimals
- Converting Recurring Decimals to Fractions
- Conversion Charts
- Practice Questions (With Solutions)
- Closing Thoughts
- Frequently Asked Questions
- What is Arithmetic Mean?
- Arithmetic Mean Formula- Ungroup Data & Group Data
- Merits of Arithmetic Mean
- Demerits of Arithmetic Mean
- Alternatives to Arithmetic Mean
- What is the Weighted Arithmetic Mean?
- Arithmetic vs. Geometric Mean
- Arithmetic Mean Application in Statistical Analysis
- Arithmetic Mean Practice Questions with Explanation
- Frequently Asked Questions
- What is Geometric Progression?
- Key Properties of Geometric Progression
- General Form Of Geometric Progression
- General Term or the Nth Term of Geometric Progression
- The sum of nth Terms of GP
- Types Of Geometric Progression
- Solved Questions and Answers of GP
- Conclusion
- Frequently Asked Questions (FAQs)
- Average in Maths
- Average Formula in Maths
- Differentiating Types of Average
- How to Calculate Average of Negative Numbers?
- Practical Applications of Averages
- Average Questions For Practice
- Frequently Asked Questions
- What is Simple Interest in Maths?
- Simple Interest Formula Explained
- Simple Interest Formula for Years, Months & Days
- Simple Interest Examples & Practice Questions
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Mathematical Ratios
- Understanding Proportions Fundamentals
- Differentiating Ratios from Proportions
- Ratio and Proportion Formulas
- Properties of Ratio and Proportion
- How to Solve Ratio and Proportion Problems
- Ratio and Proportion Problems (With Solutions)
- Summary
- Frequently Asked Questions
- What is Number in Maths?
- Types of Numbers With Example
- Real vs Complex Numbers Explored
- Basic Operations on Numbers
- Practice Questions (With Solutions)
- Frequently Asked Questions
- What is Arithmetic Progression (AP) in Maths?
- Important Terminologies in Arithmetic Progression
- Basic Terms in Arithmetic Progression
- General Form Of Arithmetic Progression Series
- Types Of Arithmetic Progression
- Solved Questions With Explanation (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Basic Concept
- Importance Of Train Problems In Aptitude
- Tips To Solve Train Problems
- Selected Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition Of Mode
- Calculating Mode For Ungrouped Data
- Calculating Mode For Grouped Data
- Bimodal, Trimodal & Multimodal Distributions
- Comparing Mean, Median & Mode
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Important Concept In Races And Games
- Calculating Time, Speed & Distance
- Importance Of Races And Games Problems
- Sample Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Types Of Partnership
- Formula For Partnership Questions
- Tips To Solve Partnership Aptitude Questions
- Selected Partnership Questions (Practice MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
HCF And LCM Methods: Formula, Practice Questions And Answers
Exploring the realm of mathematics, the concepts of Highest Common Factor (HCF) and Lowest Common Multiple (LCM) play crucial roles in problem-solving and arithmetic operations.
Understanding these fundamental principles is key to simplifying fractions, solving equations, and tackling complex mathematical challenges with precision.
Defining HCF And LCM
HCF stands for Highest Common Factor and refers to the largest number that divides two or more numbers without leaving a remainder. The HCF is used when simplifying fractions, finding equivalent fractions, or reducing ratios.
LCM stands for Lowest Common Multiple and refers to the least common denominator that signifies the smallest multiple, which is a common multiple of two or more numbers. LCM comes into play when adding or subtracting fractions with different denominators or solving problems related to periodic events like time intervals or cycles.

Calculation Methods Of HCF And LCM
Let us understand how to find LCM and HCF, i.e the different calculation methods:
Division Method Of HCF
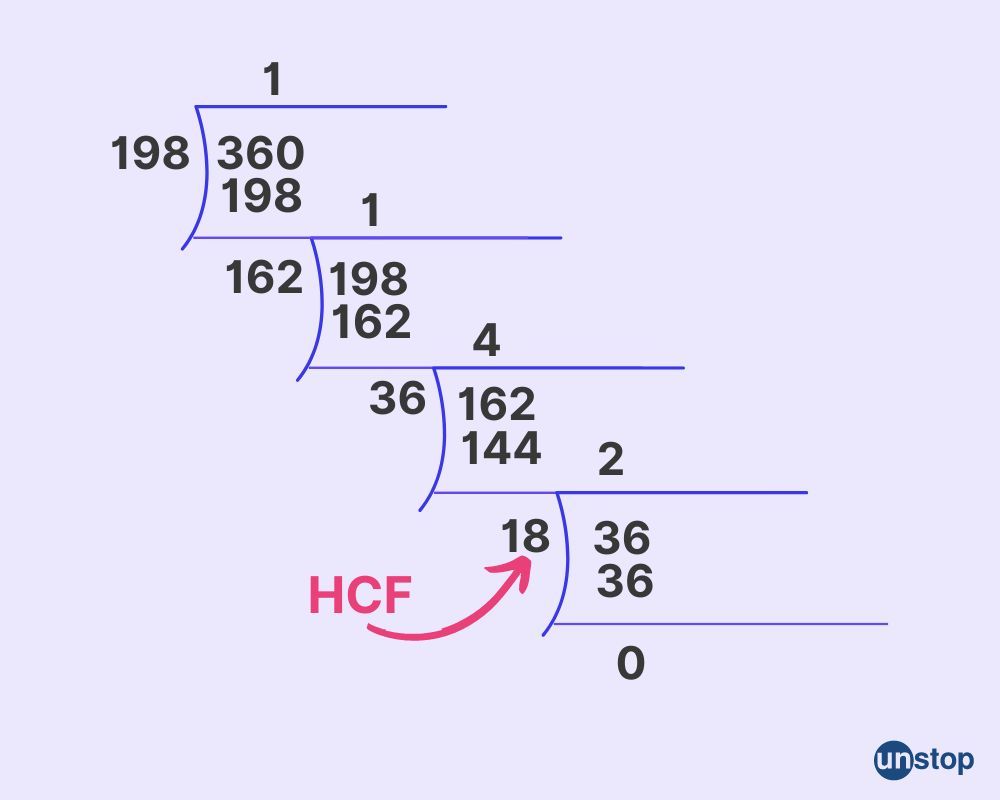
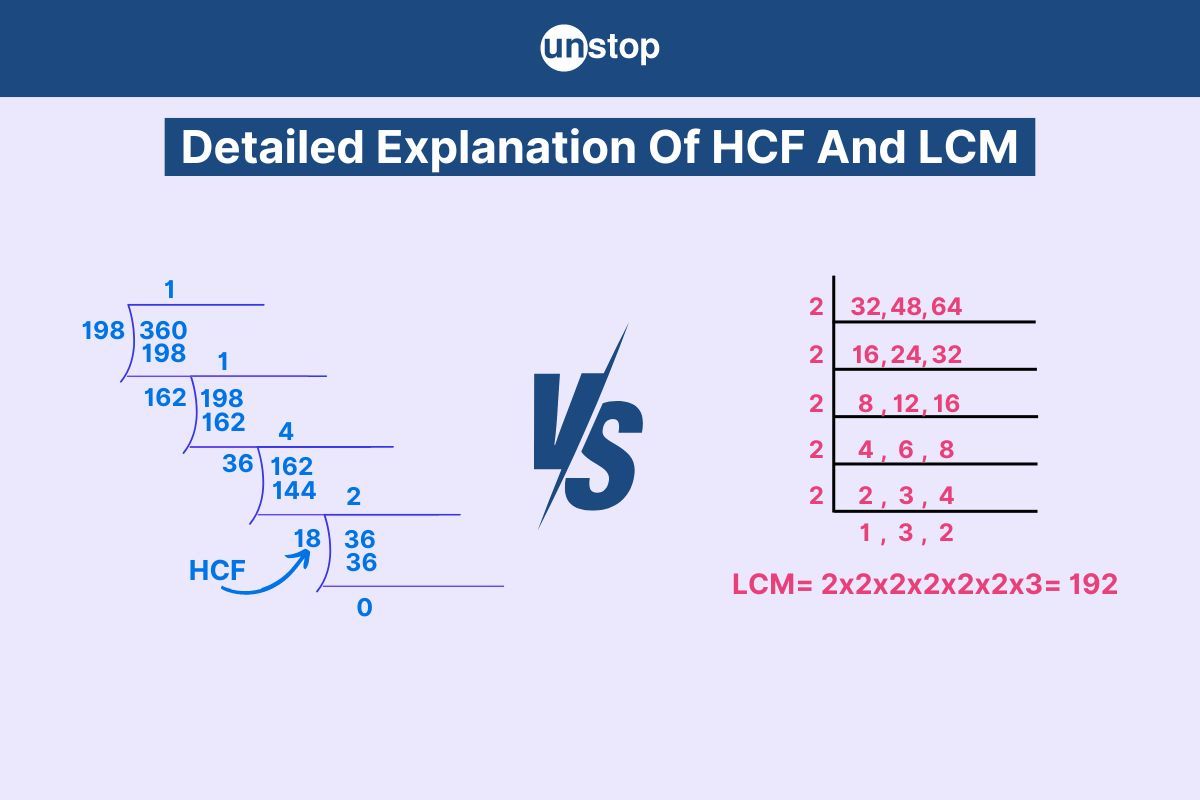
When determining the HCF using the division method, you repeatedly divide the larger number by the smaller number until you get a remainder of zero. The last divisor before reaching zero is the HCF.
For example, divide 36 by 24, which gives us a quotient of 1 and a remainder of 12. Next, divide 24 by 12. It gives us a quotient of 2 and a remainder of 0. Since we reached a remainder of zero, the last divisor used, which is 12, is the HCF of 24 and 36.
Calculation Method Of LCM through Division

To find LCM through division, multiply the two numbers and divide them by their HCF to get the LCM. This method is efficient and straightforward for both HCF and LCM calculations.
For example, if we want to find the LCM of 12 and 18 using the division method, first, we calculate the HCF of 12 and 18, which is 6. Then, we multiply the two numbers (12 * 18 = 216) and divide them by their HCF (216 / 6 = 36). Hence, 36 is the LCM of 12 and 18. This method simplifies the process of finding both the HCF and LCM efficiently.
Click here to enhance and upskill your quantitative aptitude by exploring different topics, including HCF and LCM.
HCF And LCM By Prime Factorization Method
HCF
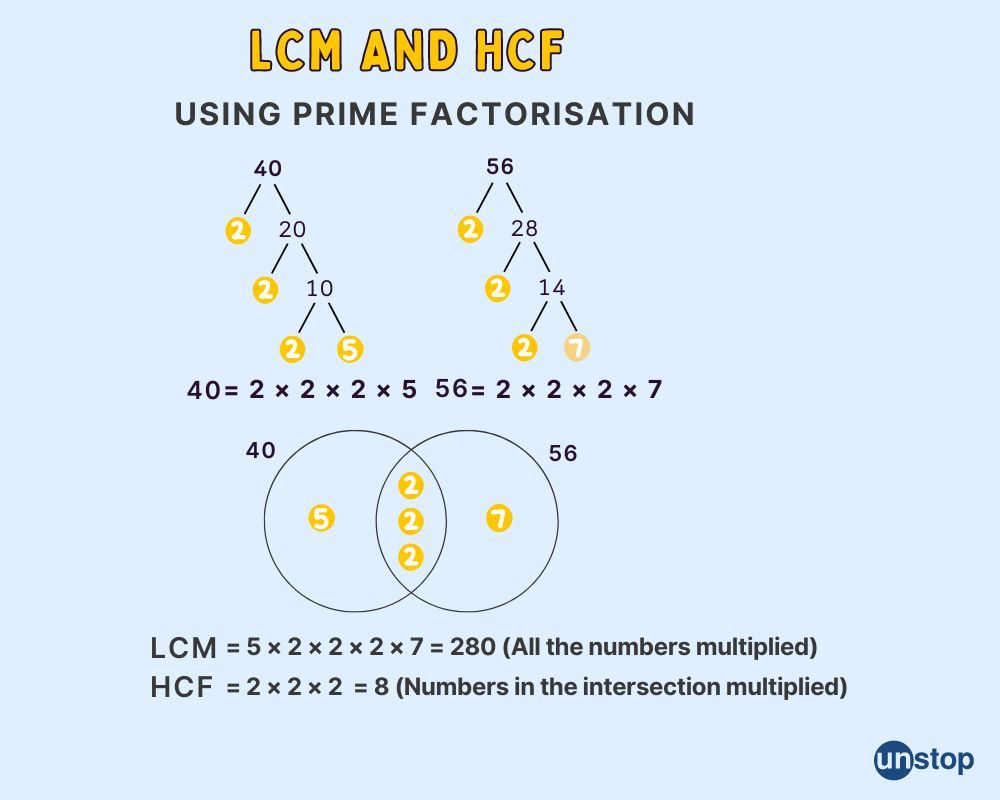
To find the HCF using prime factorization, each number is expressed as a product of its prime factors. Then, identify the common prime factors among the numbers.
Next, multiply these common prime factors to obtain the HCF of the given numbers. This method simplifies complex calculations and ensures accuracy in determining the highest common factor.
For instance, consider finding the HCF of 24 and 36. By listing their prime factors (24 = 2 x 2 x 2 x 3) and (36 = 2 x 2 x 3 x 3), we identify that the common factors are 2 and 3. Multiplying these gives us an HCF of 12.
LCM
To find the least common multiple (LCM) using prime factorization, you first need to list down the prime factors of each number. Then, identify the highest power of every prime factor present in any of the numbers. Finally, multiply these highest powers together to get the LCM.
For instance, consider finding the LCM of 12 and 18. Here, we have 2 and 3 as the prime factors of 12 and 18, respectively. By selecting the highest power of each prime factor (2^2 * 3), we get an LCM of 12.
Using the prime factorization method to calculate HCF and LCM is essential as it provides a systematic and efficient way to find the highest common factor and the least common multiple of numbers. This method breaks down numbers into their prime factors, making it easier to identify the common factors and multiples, ultimately simplifying the calculation process.
Difference Between HCF And LCM
Let us study some of the specific differences between HCF and LCM:
| Category | HCF | LCM |
|---|---|---|
| Definition | HCF is the largest number that divides two or more numbers without leaving a remainder. | LCM is the smallest number divisible by two or more numbers without leaving a remainder. |
| Use | HCF is used to simplify fractions. | LCM is used to find a common denominator for fractions. |
| Relation to set of numbers | HCF is always less than or equal to the smallest number in the set of numbers. | LCM is always greater than or equal to the largest number. |
| Alternate Names | HCF is also known as GCD (Greatest Common Divisor). | LCM is also known as LCD (Least Common Denominator). |
HCF & LCM Practice Questions With Answers
Practice is the key to excelling in HCF and LCM! Provided below are some important selected questions with detailed answers:

Question 1: What is the highest common factor of 24 and 36?
a) 4
b) 8
c) 12
d) 16
Solution: c) 12
Explanation: 24=2×2×2×3
36=2×2×3×3
HCF=2×2×3
HCF=12
Question 2: Calculate the least common multiple of 9 and 15.
a) 15
b) 27
c) 45
d) 135
Solution: c) 45
Explanation: 9=3×3
15=3×5
LCM=3×3×5
LCM=45
Question 3: Calculate the HCF of 28 and 42.
a) 2
b) 6
c) 14
d) 84
Solution: c) 14
Explanation: 28=2×2×7
42=2×3×7
HCF=2×7
HCF=14
Question 4: What is the smallest positive integer that is a multiple of 127, has a prime number of positive divisors, and has a sum of digits equal to 10?
a) 101
b) 127
c) 152
d) 169
Solution: b) 127
Explanation: (i) The number 127 is a multiple of 127 itself
(ii) The number 127 has two positive divisors = 1 and 127, and "2" is a prime number
(iii) The sum of integers of 127 is 1+2+7=10.
Question 5: If the product of two numbers is 4576 and their HCF is 16, what is their LCM?
a) 143
b) 286
c) 572
d) 1144
Solution: b) 286
Explanation: Product of numbers=HCF×LCM
4576=16×LCM
LCM=286
Question 6: The product of three distinct positive integers is 120. The sum of their reciprocals is 47/20. What is the sum of the three integers?
a) 141
b) 26
c) 27
d) None of the above
Solution: d) None of the above
Question 7: The HCF of two numbers is 42. If their LCM is 2520 and one of the numbers is 630, what is the other number?
a) 105
b) 126
c) 210
d) 168
Solution: d) 168
Explanation: Product of numbers=HCF×LCM
a×630=42×2520
a=105840/630
a=168
Question 8: Find the sum of all positive integers less than 1000 that have an odd number of factors.
a) 1,960
b) 3,936
c) 10,416
d) 15,708
Solution: c) 10,416
Explanation: A positive integer has an odd number of factors if and only if it is a perfect square.
The largest perfect square less than 1000 is 961. Therefore sum of all numbers having an odd number of factors is
=1^2+2^2+3^2 -------- 31^2
=n(n+1)(2n+1)/6 .......... where n=31
=31×32×63/6
=62,496/6
=10,416
Question 9: Find the number of positive divisors of the number 25×34×53×72.
a) 360
b) 720
c) 800
d) 900
Solution: a) 360
Explanation: If the prime factorization of a number is p1^n1×p2^n2×p3^n3×…×pk^nk, where p1,p2,…, pk are distinct primes and n1,n2,…,nk are their respective powers, then the number of positive divisors of the number is (n1+1)(n2+1)(n3+1)…(nk+1).
Number of positive divisors = (5+1)×(4+1)×(3+1)×(2+1)
=6×5×4×3
=360
Question 10: Find the LCM of 8 and 12.
a) 16
b) 24
c) 32
d) 48
Solution: b) 24
Explanation: 8=2×2×2
12=2×2×3
LCM=2×2×2×3
LCM=24
Conclusion
The comprehensive exploration of HCF and LCM has shed light on their definitions, calculation methods, and practical applications. By delving into prime factorization and division methods for both concepts, a solid foundation has been laid for understanding their significance in mathematics.
The examples provided have illustrated how these principles are applied in real-world scenarios, emphasizing the relationship between HCF and LCM. Moving forward, readers are encouraged to tackle the practice problems to solidify their understanding and mastery of these concepts.
Time For A Short Quiz
Frequently Asked Questions (FAQs)
1. Give the HCF and LCM full form and explain their significance in mathematics.
Understanding HCF (Highest Common Factor) and LCM (Least Common Multiple) is crucial in simplifying fractions, solving word problems, and analyzing relationships between numbers. It forms the foundation for various mathematical operations and helps in problem-solving strategies.
2. How are HCF and LCM calculated using prime factorization?
To find HCF by prime factorization, list the prime factors common to all numbers with the lowest power. For LCM, multiply all unique prime factors with their highest powers present in any number. The prime factorization method simplifies calculations and ensures accuracy in determining HCF and LCM.
3. What is the division method for calculating HCF?
The division method involves dividing two numbers successively to find their remainder until the remainder becomes zero. The divisor at this point is the HCF of those two numbers. This method provides a systematic approach to determine the highest common factor efficiently.
4. Why are examples and applications important when learning about HCF and LCM?
Examples and applications help reinforce understanding by demonstrating real-world scenarios where knowledge of HCF and LCM is applied. By practicing with diverse examples, learners can grasp concepts better, improve problem-solving skills, and appreciate the practical relevance of these mathematical principles.
5. How does understanding the relationship between HCF and LCM benefit problem-solving skills?
Recognizing the connection between HCF and LCM enables efficient problem-solving strategies by leveraging their properties. Understanding that LCM is a multiple of any number's factors while HCF divides them allows for quicker identification of solutions in various mathematical contexts.
Suggested reads:
- Decimal To Fraction Conversion Guide (+ Solved Questions)
- Decimal Fraction: Find Types, Operations & Practice Questions
- Difference Between Simple Interest And Compound Interest Formula
- Profit And Loss- Basic Concepts, Formulas, Questions & Answers
- Time, Speed And Distance- Formula With Aptitude Question & Answer
Instinctively, I fall for nature, music, humor, reading, writing, listening, traveling, observing, learning, unlearning, friendship, exercise, etc., all these from the cradle to the grave- that's ME! It's my irrefutable belief in the uniqueness of all. I'll vehemently defend your right to be your best while I expect the same from you!
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter
















Comments
Add comment