- Step 1: The Groundwork
- Step 2: The Three Sections
- Step 3: Practice Makes Improvement
- The Secret Ingredient
- Understanding Basics Of Number Series
- Types Of Number Series Reasoning Questions
- Addition & Multiplication In Number Series
- Square & Cube-Based Number Series Patterns
- Missing Terms & Arranging Sequences
- Tricks & Tips For Solving Number Series
- Selected Number Series Questions With Solutions
- Frequently Asked Questions (FAQs)
- Must Know Terminologies in Blood Relation Questions
- Basic Approaches to Solve Blood Relation Questions
- Types Of Blood Relation Questions
- Tips For Solving Blood Relation Questions
- Multiple Choice Questions (MCQs) with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Letter Series In Logical Reasoning
- Types Of Letter Series Patterns
- Tips For Solving Letter Series Reasoning
- Best Practice Question Samples With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basics of Problems On Age-Related Questions
- Formula to Solve Problems on Ages-Related Questions
- Types of Age-Related Questions & Examples
- Tips & Tricks for Solving Ages Problems
- Best MCQs on Problems on ages with solved answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition of Calendar
- Understanding Days of the Week
- What is a Leap Year?
- Concept of Odd Days in a Century
- Tips For Solving Calendar Reasoning Questions
- Best Calendar Reasoning Questions with Answers (MCQs)
- Frequently Asked Questions (FAQs)
- Basic Concepts of Clock
- Structure of a Clock
- Angle Equilavalence in Clock
- Tips For Solving Clock Questions
- Selected Clock Questions & Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding The Concept Of Direction Sense
- Tips For Effective Problem-Solving In Direction Sense
- Practical Test Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Dice Reasoning
- Dice Numbers In Dice Reasoning
- Classification Of Dice
- Constructed Vs Deconstructed Dice
- Tricks & Tips For Solving Dice Problems
- Practice MCQs With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Alphanumeric Series Defined
- Alphanumeric Series In Reasoning Tests
- Tips & Strategies For Solving Alphanumeric Series
- Practice Sample Questions With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept Of Mirror Image Reasoning Explained
- Important Terms In Mirror Image Reasoning
- Types Of Mirror Images
- Identifying Correct Mirror Image
- Finding Clock's Mirror Image
- Tips To Solve Mirror Images
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept & Overview Of Input-Output
- Input-Output In Competitive Exams
- Types Of Input-Output Problems
- Strategies, Tips & Tricks For Solving Reasoning Questions
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Finding The Odd One Out
- Tricks And Tips
- How to Find The Odd One Out?
- Solved MCQs with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Key Concepts
- Exploring Different Ranking Types
- Formula And Application Of Order And Ranking
- Tips For Solving Order & Ranking
- Selected Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Pipes & Cistern Aptitude
- Key Terminologies used in Pipes and Cisterns
- Pipes and Cisterns Formula with Examples
- Pipes and Cisterns Shortcut Tricks
- Tips For Solving Pipes & Cistern Problems
- Selected Questions & Answers For Practice (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Key Concept in Boats and Streams
- Formulas Of Boats & Streams
- Distance & Time Formula
- Tips For Solving Boats & Streams Questions
- Selected Practice Questions With Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept of Mixture and Alligation
- Types Of Alligation Questions
- Formula for Solving Mixture & Alligation
- Tips For Solving Mixture And Alligation
- Selected Questions With Answers For Practice
- Conclusion
- Frequently Asked Questions (FAQs)
- Concepts and Definitions Related to Time and Work
- Important Time And Work Formulas
- Tricks and Tips to Solve Time & Work Questions
- Time And Work MCQs with Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Harmonic Progression(HP)?
- Formula to find the nth Term in Harmonic Progression
- Formula to find the Sum of the nth Term in HP
- What is Harmonic Mean?
- Harmonic Progression Solved Best MCQs
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Mensuration in Maths?
- What are 2D figures in Mensuration?
- What are 3D figures in Mensuartion?
- Basic Terminologies In Mensuration
- Basic 2D Formulas in Mensuration
- Basic 3D Formulas in Mensuration
- 2D vs 3D in Mensuration
- Solved Questions With Solutions (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Relationship Between Time, Speed And Distance
- Conversion Units Time, Speed And Distance
- Average & Relative Speed: Two Trains Moving in the same or opposite direction
- Solved MCQs on Time, Speed And Distance
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Simplification in Maths?
- BODMAS Rule in Simplification Explained
- Simplification & Approximation Relation
- Key Terms in Simplification
- Examples Of Simplification Techniques
- Simplification Questions With Solved Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Height And Distance Important Terms
- Right Angled Triangle In Trigonometry
- Trigonometric Ratios
- Solved Examples For Better Understanding
- Height And Distance Applications In Trigonometry
- Height And Distance Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Interest Types
- Simple Interest Vs. Compound Interest
- Selected Solved Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basic Concepts Of Profit And Loss
- Determining Selling Price
- Calculating Discounts
- Formulas For Calculating Profit And Loss
- Examples Of Profit And Loss
- Profit & Loss Questions With Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Angle Of Elevation
- Key Terms Used In Angle Of Elevation
- Angle of Elevation Formula with Example
- Angle of Elevation vs. Angle of Depression
- Angle of Elevation MCQs with Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining HCF And LCM
- Calculation Methods Of HCF And LCM
- HCF By Prime Factorization Method
- LCM By Prime Factorization Method
- Difference Between HCF And LCM
- HCF & LCM Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- What is fraction and decimal?
- Understanding Decimal Fraction
- Place Value in Decimal Fraction
- Mathematical Operations with Decimal Fraction
- Practice with Solved Examples
- Summary
- Frequently Asked Questions
- All About Decimals
- All About Fractions
- How to Convert a Decimal into Fraction
- Simple vs Recurring Decimals
- Converting Recurring Decimals to Fractions
- Conversion Charts
- Practice Questions (With Solutions)
- Closing Thoughts
- Frequently Asked Questions
- What is Arithmetic Mean?
- Arithmetic Mean Formula- Ungroup Data & Group Data
- Merits of Arithmetic Mean
- Demerits of Arithmetic Mean
- Alternatives to Arithmetic Mean
- What is the Weighted Arithmetic Mean?
- Arithmetic vs. Geometric Mean
- Arithmetic Mean Application in Statistical Analysis
- Arithmetic Mean Practice Questions with Explanation
- Frequently Asked Questions
- What is Geometric Progression?
- Key Properties of Geometric Progression
- General Form Of Geometric Progression
- General Term or the Nth Term of Geometric Progression
- The sum of nth Terms of GP
- Types Of Geometric Progression
- Solved Questions and Answers of GP
- Conclusion
- Frequently Asked Questions (FAQs)
- Average in Maths
- Average Formula in Maths
- Differentiating Types of Average
- How to Calculate Average of Negative Numbers?
- Practical Applications of Averages
- Average Questions For Practice
- Frequently Asked Questions
- What is Simple Interest in Maths?
- Simple Interest Formula Explained
- Simple Interest Formula for Years, Months & Days
- Simple Interest Examples & Practice Questions
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Mathematical Ratios
- Understanding Proportions Fundamentals
- Differentiating Ratios from Proportions
- Ratio and Proportion Formulas
- Properties of Ratio and Proportion
- How to Solve Ratio and Proportion Problems
- Ratio and Proportion Problems (With Solutions)
- Summary
- Frequently Asked Questions
- What is Number in Maths?
- Types of Numbers With Example
- Real vs Complex Numbers Explored
- Basic Operations on Numbers
- Practice Questions (With Solutions)
- Frequently Asked Questions
- What is Arithmetic Progression (AP) in Maths?
- Important Terminologies in Arithmetic Progression
- Basic Terms in Arithmetic Progression
- General Form Of Arithmetic Progression Series
- Types Of Arithmetic Progression
- Solved Questions With Explanation (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Basic Concept
- Importance Of Train Problems In Aptitude
- Tips To Solve Train Problems
- Selected Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition Of Mode
- Calculating Mode For Ungrouped Data
- Calculating Mode For Grouped Data
- Bimodal, Trimodal & Multimodal Distributions
- Comparing Mean, Median & Mode
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Important Concept In Races And Games
- Calculating Time, Speed & Distance
- Importance Of Races And Games Problems
- Sample Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Types Of Partnership
- Formula For Partnership Questions
- Tips To Solve Partnership Aptitude Questions
- Selected Partnership Questions (Practice MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
Clock Questions: Basic Concepts & Aptitude Questions (MCQs) Explained

Understanding the concept and questions on clocks is essential for tackling questions in almost all competitive examinations. This topic plays a crucial role in logical reasoning, requiring both thorough analytical skills and precise calculations to arrive at accurate answers.
Basic Concepts of Clock
The clock face consists of the hour hand, the minute hand, and the second hand. These elements work together to indicate time accurately. Horology is the field that focuses on the study of clocks.
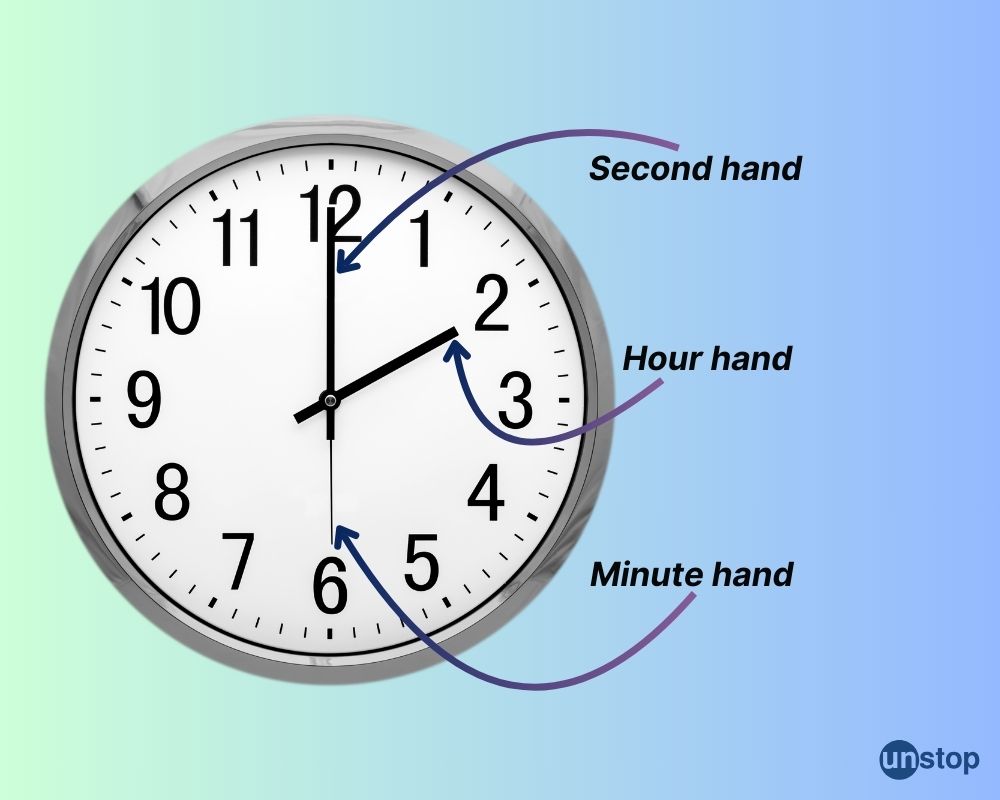
Structure of a Clock
A clock is made up of 360°, which is split into 12 equal parts. To find the angle between each part, you divide the total angle of the clock, which is 360°, by the number of sections, which is 12.
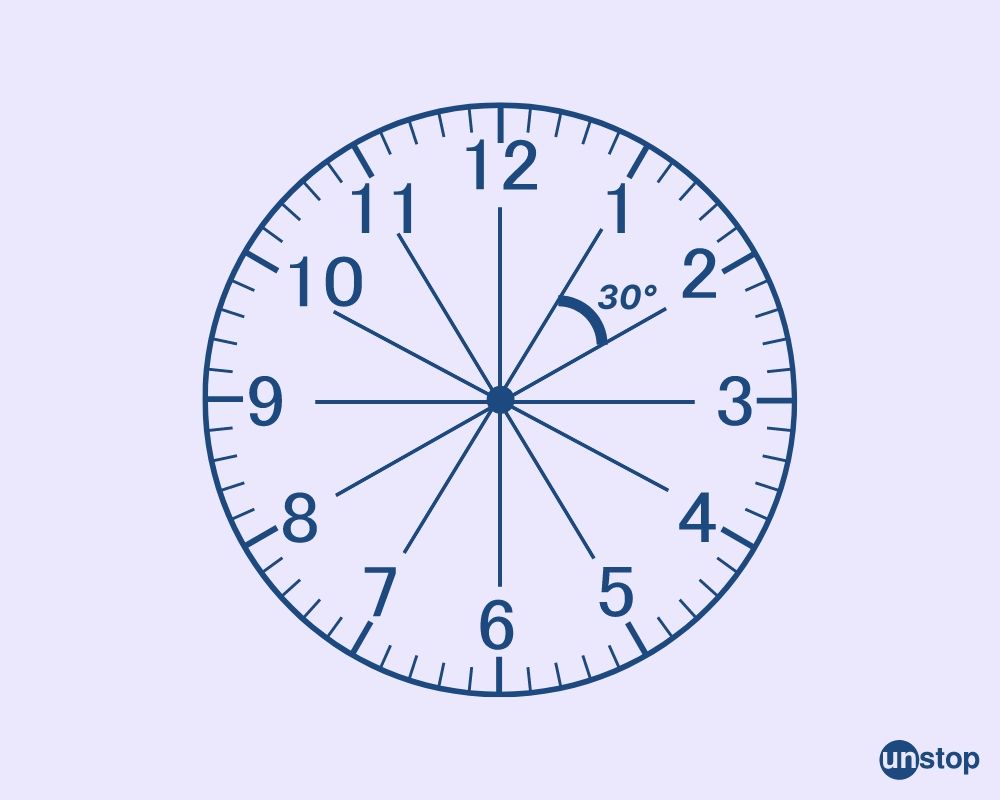
The angle between any two consecutive divisions = 360°/12= 30°
Angular Value of a Minute in a Clock
The angular value of a minute in a clock refers to the angle covered by the minute hand as it moves between minute markers. Since a clock is a circle, which is 360 degrees, we can calculate the angular movement for each minute by dividing the full 360 degrees by the 60 minutes in one hour.
Formula for Angular Value
The angular value of a minute in a clock refers to the angle covered by the minute hand as it moves between minute markers. Since a clock is a circle, which is 360 degrees, we can calculate the angular movement for each minute by dividing the full 360 degrees by the 60 minutes in one hour.
Angular value per minute=360°/60°=6°
- A clock is a circle, so it has 360 degrees.
- The minute hand completes one full rotation (360 degrees) in 60 minutes.
- Therefore, each minute, the minute hand moves by 6 degrees.
So, the angular value of a minute on a clock is 6 degrees.
The speed of a minute hand
In one hour, the minute hand of a clock makes a complete rotation of 360°. This means it moves across all 12 sections of the clock face during that time. Since there are 60 minutes in an hour, the speed of the minute hand can be calculated as (360°)/(60 minutes).
Speed of a minute hand = 6° per minute
The speed of an hour hand
The hour hand moves at an angle of 30 degrees every hour. This means it covers the distance between each division on the clock face, which represents 5 minutes, within a span of 60 minutes. Therefore, the speed of the hour hand can be calculated as 30 degrees divided by 60 minutes, which equals 1/2 ° per minute.
Click here to enhance and upskill your quantitative and reasoning prowess consistently. It provides study resources, ensuring quality over quantity.
Angle Equilavalence in Clock
Understanding minute angle equivalence is vital for accurately calculating time-related angles. Here is the tabular representation of the angle in relation to the minute’s hand in a clock:
| Minutes | Angular Value (In degree) |
| 1 minute | 6° |
| 2 minutes | 12° |
| 3 minutes | 18° |
| 4 minutes | 24° |
| 5 minutes | 30° |
| 6 minutes | 36° |
| 7 minutes | 42° |
| 8 minutes | 48° |
| 9 minutes | 54° |
| 10 minutes | 60° |
| 15 minutes | 90° |
| 30 minutes | 180° |
| 60 minutes | 360° |
Tips For Solving Clock Questions

Let us study some of the tips for solving clock problems:
Angle Calculation
To quickly determine the angle between a clock's hour and minute hands, multiply the difference in hours by 30 degrees.
Pattern Recognition
Identifying recurring patterns in clock problems can streamline your problem-solving process. Look for symmetrical positions like 3:15 and 9:45, which form right angles.
Selected Clock Questions & Answers (MCQs)

Here, we provide you with a set of selected questions with detailed explanations for answers related to clock questions for placement interviews and exams:
Question 1. What is the angle between the hour and minute hands on a clock at 5:00?
a) 90 degrees
b) 120 degrees
c) 150 degrees
d) 180 degrees
Solution: At 5:00, the hour hand is exactly on the 5, and the minute hand points directly at the 12. Each hour mark represents 30 degrees on the clock face.
So, the angle covered by the hour hand from the 12 o'clock position is 5×30=150 degrees.
The minute hand points to the minute mark corresponding to the current minute. At 5:00, it's at the 12. Since it's exactly on the hour mark, the minute hand has covered 0 degrees.
To find the angle between the hands, we calculate their positions' differences. Since the hour hand is ahead of the minute hand, we subtract the minute hand's position from the hour hand's position: 150−0=150 degrees.
So, at 5:00, the angle between the minute and hour hands of the clock is 150 degrees.
Question 2. The hour and minute hands of a clock at 9:45 is
a) 22.5 degrees
b) 90 degrees
c) 112.5 degrees
d) 135 degrees
Solution: At 9:45, the hour hand is closer to the 10 than the 9 because 45 minutes have passed.
Since the hour hand moves 30 degrees in one hour and 0.5 degrees for every minute passed within an hour, we calculate its position as follows:
Hour hand angle=(9×30)+(45×0.5)=270+22.5=292.5 degrees.
The minute hand is at the 9, pointing to 45 minutes past the hour.
In one minute, the minute hand moves 6 degrees, so at 9:45, it has covered 45×6=270 degrees.
To find the angle between the hands, we calculate the absolute difference between their positions.
Since the hour hand is ahead of the minute hand, we subtract the minute hand's position from the hour hand's position: 292.5−270=22.5 degrees.
Question 3. The hour and minute hands of a clock form a right angle between 3 o'clock and 4 o'clock at
a) 3:15
b) 3:20
c) 3:30
d) 3:45
Solution: We're asked to find the time between 3 o'clock and 4 o'clock when the hour and minute hands form a right angle. This interval covers the hours between 3 and 4.
A right angle measures 90 degrees. In a clock, when the hour and minute hands form a right angle, it means the angle between them is 90 degrees.
At 3:00, the hour hand points exactly at the 3. Since the hour hand moves 30 degrees in one hour and 0.5 degrees for every minute passed within an hour, we calculate its position at each minute past 3:00 to see when it forms a right angle with the minute hand.
At 3:00, the minute hand points exactly at the 12. In one minute, the minute hand moves 6 degrees, so we calculate its position at each minute past 3:00. At each minute past 3:00, we check if the angle between the hour and minute hands is 90 degrees.
We go through the options given (3:15, 3:20, 3:30, 3:45) and determine which one satisfies the condition of the hour and minute hands forming a right angle within the 3-4 o'clock interval.
We find that at 3:45, the hour hand is at the 3, and the minute hand is pointing directly at the 9, forming a right angle with the hour hand.
Question 4. In a clock, the hour and minute hands will be aligned between 4 and 5 o'clock at
a) 4:00
b) 4:15
c) 4:30
d) 4:45
Solution: We're asked to find the time between 4 o'clock and 5 o'clock when the hour and minute hands of a clock are aligned. This interval covers the hours between 4 and 5.
When the hour and minute hands of a clock are aligned, they are pointing in the same direction, indicating the same minute mark.
At 4:00, the hour hand points exactly at the 4. Since the hour hand moves 30 degrees in one hour and 0.5 degrees for every minute passed within an hour, we calculate its position at each minute past 4:00 to see when it aligns with the minute hand.
At 4:00, the minute hand points exactly at the 12. In one minute, the minute hand moves 6 degrees, so we calculate its position at each minute past 4:00. At each minute past 4:00, we check if the hour and minute hands are pointing to the same minute mark.
When we find the time, the hour and minute hands align, that's our answer. We go through the options given (4:00, 4:15, 4:30, 4:45) and determine which one satisfies the condition of the hour and minute hands being aligned within the 4-5 o'clock interval.
We find that at 4:30, the hour hand is halfway between the 4 and the 5, and the minute hand is also pointing at the 6, indicating 30 minutes past the hour. Therefore, the hour and minute hands are aligned.
Question 5. A clock is set correctly at 5:00 a.m. on a Monday. However, the clock loses 16 minutes every 24 hours. By the time the clock shows 10:00 p.m. on Thursday, what will be the true time?
a) 10:15 pm
b) 10:59 pm
c) 10:30 pm
d) 10:00 pm
Solution: From 5:00 a.m. Monday to 10:00 p.m. Thursday is 89 hours. The clock loses 16 minutes every 24 hours, which is 2/3 minutes per hour.
Over 89 hours, it loses: 89×2/3=59.33 minutes
So, when the clock shows 10:00 p.m., the true time is 10:59 p.m.
Question 6. The angle between the hour and minute hands at 6:45 is
a) 15 degrees
b) 22.5 degrees
c) 30 degrees
d) 67.5 degrees
Solution: At 6:45, the hour hand is exactly on the 7, but it has moved slightly past 6 due to the 45 minutes passed. The hour hand moves 30 degrees in one hour and 0.5 degrees for every minute passed within an hour.
So, at 6:45, the angle covered by the hour hand is:
Hour hand angle=(6×30)+(45×0.5)=180+22.5=202.5 degrees
At 6:45, the minute hand points directly to the 9, representing 45 minutes past the hour. In one minute, the minute hand moves 6 degrees, so at 6:45, the angle covered by the minute hand is 45×6=270 degrees.
To find the angle between the hands, we calculate the absolute difference between their positions.
Since the hour hand is behind the minute hand, we subtract the hour hand's position from the minute hand's position: 270−202.5=67.5 degrees. So, at 6:45, the angle between the hour and minute hands of the clock is 67.5 degrees.
Question 7. The angle between the hour and minute hands at 10:30 is
a) 45 degrees
b) 75 degrees
c) 105 degrees
d) 135 degrees
Solution: At 10:30, the hour hand is exactly on the 10, but it has moved slightly past 10 due to the 30 minutes passed. The hour hand moves 30 degrees in one hour and 0.5 degrees for every minute passed within an hour.
So, at 10:30, the angle covered by the hour hand is:
Hour hand angle=(10×30)+(30×0.5)=300+15=315 degrees
At 10:30, the minute hand points directly to the 6, representing 30 minutes past the hour. In one minute, the minute hand moves 6 degrees, so at 10:30, the angle covered by the minute hand is 30×6=180 degrees.
To find the angle between the hands, we calculate the absolute difference between their positions. Since the hour hand is behind the minute hand, we subtract the hour hand's position from the minute hand's position: 180−315=135 degrees. So, at 10:30, the angle between the hour and minute hands of the clock is 135 degrees.
Question 8. At what time between 1 and 2 o'clock will a clock's hour and minute hands be closest together?
a) 1:05
b) 1:15
c) 1:30
d) 1:45
Solution: We're asked to find the time between 1 o'clock and 2 o'clock when the hour and minute hands of a clock are closest together. This interval covers the hours between 1 and 2. The rate at which the angle between the hour and minute hands changes is not constant but varies as time progresses.
At 1:00, the hour hand points directly to the 1, and the minute hand points to the 12, overlapping with the hour hand. The angle between the hour and minute hands is 0 degrees at this time.
To find when the hour and minute hands are closest together, we need to determine when the difference between their positions is smallest.
We go through the options given (1:05, 1:15, 1:30, 1:45) and determine which one satisfies the condition of the hour and minute hands being closest together within the 1-2 o'clock interval.
We find that at 1:15, the hour hand has moved slightly past the 1, and the minute hand has moved away from the 12. This time is when the hour and minute hands are closest together.
Question 9. The hour and minute hands form a right angle between 3 o'clock and 4 o'clock at
a) 3:05
b) 3:15
c) 3:30
d) 3:45
Solution: We're asked to find the time between 3 o'clock and 4 o'clock when the hour and minute hands of a clock form a right angle. This interval covers the hours between 3 and 4.
A right angle between the hour and minute hands of a clock occurs twice in every hour: once when the minute hand is ahead of the hour hand and once when it's behind.
At 3:00, the hour hand points exactly at the 3.
Since the hour hand moves 30 degrees in one hour, we calculate its position at each minute past 3:00 to see when it forms a right angle with the minute hand. At 3:00, the minute hand points exactly at the 12.
In one minute, the minute hand moves 6 degrees, so we calculate its position at each minute past 3:00. At each minute past 3:00, we check if the angle between the hour and minute hands is 90 degrees.
We go through the options given (3:05, 3:15, 3:30, 3:45) and determine which satisfies the condition of the hour and minute hands forming a right angle within the 3-4 o'clock interval.
Therefore, the hour and minute hands form a right angle at 3:30.
Question 10: Between 9 o'clock and 10 o'clock, the hour and minute hands of a clock are farthest apart at
a) 9:15
b) 9:30
c) 9:45
d) 9:50
Solution: We're asked to find the time between 9 o'clock and 10 o'clock when the hour and minute hands of a clock are farthest apart. This interval covers the hours between 9 and 10. The hour and minute hands of a clock are farthest apart when they are at opposite ends of the clock face.
At 9:00, the hour hand points exactly at the 9.
Since the hour hand moves 30 degrees in one hour, we calculate its position at each minute past 9:00 to determine when it's farthest from the minute hand. At 9:00, the minute hand points exactly at the 12.
In one minute, the minute hand moves 6 degrees, so we calculate its position at each minute past 9:00. We go through the options given (9:15, 9:30, 9:45, 9:50) and determine which one satisfies the condition of the hour and minute hands being farthest apart within the 9-10 o'clock interval.
We find that at 9:50, the hour hand is close to the 10, and the minute hand is close to the 12. This time represents when the hour and minute hands are farthest apart.
Conclusion
In conclusion, one can effectively understand the practical applications of clock knowledge by exploring the speed comparison of clock hands, learning tips for efficient problem-solving, and practising selected sample questions.
Take the time to engage with the material covered, practice regularly, and explore additional resources to deepen your understanding of clock questions.
Quiz Time To Test Your Mind
Frequently Asked Questions (FAQs)
1. How can one understand the structure of a clock?
Clock structure involves the face, hands, and markings. The face has numbers or Roman numerals representing hours. The hour hand is shorter and moves slowly, while the minute hand is longer and moves faster. The second hand, if present, ticks continuously. Understanding these components aids in reading time accurately.
2. What are the essential clock formulas and concepts to grasp?
Key formulas include calculating angles between clock hands and determining time elapsed based on their positions. Concepts like the relative speed of hands and angular displacement are crucial for solving clock problems efficiently.
3. Can you explain minute angle equivalence in clocks?
Minute angle equivalence means every minute mark on a clock corresponds to 6 degrees. This principle simplifies calculating angles between the hour and minute hands at any given time by converting minutes into degrees.
4. How does one compare the speed of clock hands?
The minute hand is 12 times faster than the hour hand since it covers 360 degrees (a full circle) in an hour compared to the hour hand's 30 degrees per hour. Understanding this speed difference is vital for accurate time interpretation.
5. What are some key shortcuts for solving clock problems effectively?
Shortcuts like visualizing fractions of an hour or using multiples of 5 minutes can expedite calculations involving clock angles or time intervals. These techniques streamline problem-solving and enhance accuracy when dealing with various clock-related scenarios.
Suggested reads:
- Calendar Questions- Selected Aptitude Questions & Answers
- Pipes And Cisterns | Top Selected Question With Answer & Formula
- Problems On Age - Mastering Best Aptitude Questions & Solutions
- Letter & Symbol Series Explained- Top Selected Question & Answer
- Number Series: Top Selected Logical Reasoning Questions & Answers
Instinctively, I fall for nature, music, humor, reading, writing, listening, traveling, observing, learning, unlearning, friendship, exercise, etc., all these from the cradle to the grave- that's ME! It's my irrefutable belief in the uniqueness of all. I'll vehemently defend your right to be your best while I expect the same from you!
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter












Comments
Add comment