- Step 1: The Groundwork
- Step 2: The Three Sections
- Step 3: Practice Makes Improvement
- The Secret Ingredient
- Understanding Basics Of Number Series
- Types Of Number Series Reasoning Questions
- Addition & Multiplication In Number Series
- Square & Cube-Based Number Series Patterns
- Missing Terms & Arranging Sequences
- Tricks & Tips For Solving Number Series
- Selected Number Series Questions With Solutions
- Frequently Asked Questions (FAQs)
- Must Know Terminologies in Blood Relation Questions
- Basic Approaches to Solve Blood Relation Questions
- Types Of Blood Relation Questions
- Tips For Solving Blood Relation Questions
- Multiple Choice Questions (MCQs) with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Letter Series In Logical Reasoning
- Types Of Letter Series Patterns
- Tips For Solving Letter Series Reasoning
- Best Practice Question Samples With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basics of Problems On Age-Related Questions
- Formula to Solve Problems on Ages-Related Questions
- Types of Age-Related Questions & Examples
- Tips & Tricks for Solving Ages Problems
- Best MCQs on Problems on ages with solved answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition of Calendar
- Understanding Days of the Week
- What is a Leap Year?
- Concept of Odd Days in a Century
- Tips For Solving Calendar Reasoning Questions
- Best Calendar Reasoning Questions with Answers (MCQs)
- Frequently Asked Questions (FAQs)
- Basic Concepts of Clock
- Structure of a Clock
- Angle Equilavalence in Clock
- Tips For Solving Clock Questions
- Selected Clock Questions & Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding The Concept Of Direction Sense
- Tips For Effective Problem-Solving In Direction Sense
- Practical Test Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Dice Reasoning
- Dice Numbers In Dice Reasoning
- Classification Of Dice
- Constructed Vs Deconstructed Dice
- Tricks & Tips For Solving Dice Problems
- Practice MCQs With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Alphanumeric Series Defined
- Alphanumeric Series In Reasoning Tests
- Tips & Strategies For Solving Alphanumeric Series
- Practice Sample Questions With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept Of Mirror Image Reasoning Explained
- Important Terms In Mirror Image Reasoning
- Types Of Mirror Images
- Identifying Correct Mirror Image
- Finding Clock's Mirror Image
- Tips To Solve Mirror Images
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept & Overview Of Input-Output
- Input-Output In Competitive Exams
- Types Of Input-Output Problems
- Strategies, Tips & Tricks For Solving Reasoning Questions
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Finding The Odd One Out
- Tricks And Tips
- How to Find The Odd One Out?
- Solved MCQs with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Key Concepts
- Exploring Different Ranking Types
- Formula And Application Of Order And Ranking
- Tips For Solving Order & Ranking
- Selected Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Pipes & Cistern Aptitude
- Key Terminologies used in Pipes and Cisterns
- Pipes and Cisterns Formula with Examples
- Pipes and Cisterns Shortcut Tricks
- Tips For Solving Pipes & Cistern Problems
- Selected Questions & Answers For Practice (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Key Concept in Boats and Streams
- Formulas Of Boats & Streams
- Distance & Time Formula
- Tips For Solving Boats & Streams Questions
- Selected Practice Questions With Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept of Mixture and Alligation
- Types Of Alligation Questions
- Formula for Solving Mixture & Alligation
- Tips For Solving Mixture And Alligation
- Selected Questions With Answers For Practice
- Conclusion
- Frequently Asked Questions (FAQs)
- Concepts and Definitions Related to Time and Work
- Important Time And Work Formulas
- Tricks and Tips to Solve Time & Work Questions
- Time And Work MCQs with Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Harmonic Progression(HP)?
- Formula to find the nth Term in Harmonic Progression
- Formula to find the Sum of the nth Term in HP
- What is Harmonic Mean?
- Harmonic Progression Solved Best MCQs
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Mensuration in Maths?
- What are 2D figures in Mensuration?
- What are 3D figures in Mensuartion?
- Basic Terminologies In Mensuration
- Basic 2D Formulas in Mensuration
- Basic 3D Formulas in Mensuration
- 2D vs 3D in Mensuration
- Solved Questions With Solutions (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Relationship Between Time, Speed And Distance
- Conversion Units Time, Speed And Distance
- Average & Relative Speed: Two Trains Moving in the same or opposite direction
- Solved MCQs on Time, Speed And Distance
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Simplification in Maths?
- BODMAS Rule in Simplification Explained
- Simplification & Approximation Relation
- Key Terms in Simplification
- Examples Of Simplification Techniques
- Simplification Questions With Solved Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Height And Distance Important Terms
- Right Angled Triangle In Trigonometry
- Trigonometric Ratios
- Solved Examples For Better Understanding
- Height And Distance Applications In Trigonometry
- Height And Distance Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Interest Types
- Simple Interest Vs. Compound Interest
- Selected Solved Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basic Concepts Of Profit And Loss
- Determining Selling Price
- Calculating Discounts
- Formulas For Calculating Profit And Loss
- Examples Of Profit And Loss
- Profit & Loss Questions With Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Angle Of Elevation
- Key Terms Used In Angle Of Elevation
- Angle of Elevation Formula with Example
- Angle of Elevation vs. Angle of Depression
- Angle of Elevation MCQs with Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining HCF And LCM
- Calculation Methods Of HCF And LCM
- HCF By Prime Factorization Method
- LCM By Prime Factorization Method
- Difference Between HCF And LCM
- HCF & LCM Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- What is fraction and decimal?
- Understanding Decimal Fraction
- Place Value in Decimal Fraction
- Mathematical Operations with Decimal Fraction
- Practice with Solved Examples
- Summary
- Frequently Asked Questions
- All About Decimals
- All About Fractions
- How to Convert a Decimal into Fraction
- Simple vs Recurring Decimals
- Converting Recurring Decimals to Fractions
- Conversion Charts
- Practice Questions (With Solutions)
- Closing Thoughts
- Frequently Asked Questions
- What is Arithmetic Mean?
- Arithmetic Mean Formula- Ungroup Data & Group Data
- Merits of Arithmetic Mean
- Demerits of Arithmetic Mean
- Alternatives to Arithmetic Mean
- What is the Weighted Arithmetic Mean?
- Arithmetic vs. Geometric Mean
- Arithmetic Mean Application in Statistical Analysis
- Arithmetic Mean Practice Questions with Explanation
- Frequently Asked Questions
- What is Geometric Progression?
- Key Properties of Geometric Progression
- General Form Of Geometric Progression
- General Term or the Nth Term of Geometric Progression
- The sum of nth Terms of GP
- Types Of Geometric Progression
- Solved Questions and Answers of GP
- Conclusion
- Frequently Asked Questions (FAQs)
- Average in Maths
- Average Formula in Maths
- Differentiating Types of Average
- How to Calculate Average of Negative Numbers?
- Practical Applications of Averages
- Average Questions For Practice
- Frequently Asked Questions
- What is Simple Interest in Maths?
- Simple Interest Formula Explained
- Simple Interest Formula for Years, Months & Days
- Simple Interest Examples & Practice Questions
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Mathematical Ratios
- Understanding Proportions Fundamentals
- Differentiating Ratios from Proportions
- Ratio and Proportion Formulas
- Properties of Ratio and Proportion
- How to Solve Ratio and Proportion Problems
- Ratio and Proportion Problems (With Solutions)
- Summary
- Frequently Asked Questions
- What is Number in Maths?
- Types of Numbers With Example
- Real vs Complex Numbers Explored
- Basic Operations on Numbers
- Practice Questions (With Solutions)
- Frequently Asked Questions
- What is Arithmetic Progression (AP) in Maths?
- Important Terminologies in Arithmetic Progression
- Basic Terms in Arithmetic Progression
- General Form Of Arithmetic Progression Series
- Types Of Arithmetic Progression
- Solved Questions With Explanation (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Basic Concept
- Importance Of Train Problems In Aptitude
- Tips To Solve Train Problems
- Selected Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition Of Mode
- Calculating Mode For Ungrouped Data
- Calculating Mode For Grouped Data
- Bimodal, Trimodal & Multimodal Distributions
- Comparing Mean, Median & Mode
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Important Concept In Races And Games
- Calculating Time, Speed & Distance
- Importance Of Races And Games Problems
- Sample Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Types Of Partnership
- Formula For Partnership Questions
- Tips To Solve Partnership Aptitude Questions
- Selected Partnership Questions (Practice MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
Ratio and Proportion: Mastering Fundamentals (+ Solved Questions)

Numbers are everywhere, but it's how we relate them that unlocks their true power in quantitative aptitude. Enter ratio and proportion, the dynamic duo that lets you solve problems from calculating recipe portions to cracking complex business puzzles.
Get ready to transform from a number cruncher to a master of comparisons – this guide will equip you with the knowledge and techniques to tackle any ratio and proportion question thrown your way!
Defining Mathematical Ratios

Definition: In mathematics, a ratio is a comparison of two numbers or quantities. It is expressed as the quotient of one number divided by the other, typically written in the form a:b or a/b.
In a ratio, the first number is the antecedent, while the second is the consequent. This distinction is crucial as it determines the order in which quantities are compared.
Ratios are used to compare different quantities and can be simplified or converted to different forms for easier analysis. They are essential in various mathematical concepts, such as proportions, percentages, and rates.
Ratios provide a way to understand the relationship between two values and are commonly used in solving real-world problems across different fields of study. For instance, if a recipe requires 2 cups of flour and 1 cup of sugar, the ratio of flour to sugar is 2:1. This comparison helps maintain the right balance in the recipe.
Ratio Sign & Representation
Ratios can be represented in various ways, such as using the phrase "a to b" or the symbol "a : b". Both forms convey the same information but offer flexibility in how ratios are expressed.
When discussing ratios, it is important to consider the ratio sign, which indicates the relationship between the two quantities being compared. The ratio sign can be represented as a colon (:) or a fraction (/), with the first quantity being compared to the second.
Understanding Proportions Fundamentals
Definition: A proportion in math is a statement that expresses the equality of two ratios. It indicates that two comparisons of quantities are equivalent. This is often written using a colon (:) or an equal sign (=).
For example, 2:3 = 8:12 is a proportion, stating that the ratio of 2 to 3 is the same as the ratio of 8 to 12.
Direct vs. Inverse Proportion
In direct proportion, as one quantity increases, the other also increases at a consistent rate. For example, if the number of workers doubles, the time taken to complete a task is halved.
Conversely, in inverse proportion, as one quantity increases, the other decreases at a constant rate. A classic example is the relationship between speed and time: the faster you drive (increase in speed), the less time it takes to reach a destination (decrease in time).
Continued Proportion Examples
Continued proportion involves three or more quantities where the ratio of consecutive pairs remains constant. For instance:
- If 2:4 equals 3:6 and 4:8 equals 5:10, then these are continued proportions.
- Another example could be 1:2 equals 2:4 equals 4:8 equals 8:16.
Illustrative Proportion Examples
- Direct Proportion: Consider a scenario where buying more apples results in a lower cost per apple; this demonstrates direct proportionality.
- Inverse Proportion: Imagine driving at a constant speed; the longer you drive, the further you travel inversely proportional to your speed.
- Continued Proportion: If you mix sugar and water in ratios like 1:2, 2:4, and so on while maintaining consistency, you have continued proportions.
Differentiating Ratios from Proportions
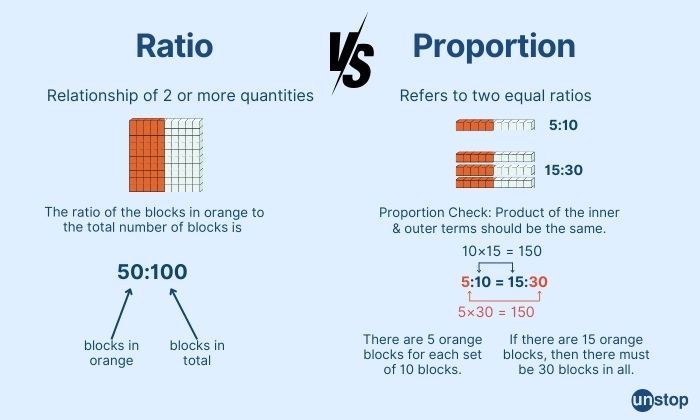
Definitions
Ratios represent the relationship between two quantities, showing how many times one value contains or is contained within another. Proportions, on the other hand, are equations stating that two ratios are equivalent.
Ratios can be standalone comparisons, such as "the ratio of boys to girls in a class is 2:3," without forming a proportion. In this case, there's no requirement for equality between two separate ratios.
Necessity of Equality
The critical distinction lies in the necessity of equality within proportions compared to ratios.
While ratios simply compare quantities, proportions demand that these comparisons maintain an equal relationship. In mathematical terms, proportions require that the cross products are equal. This means that when expressing proportions as fractions (a/b = c/d), the product of ad must equal bc for the equation to hold true.
Scenarios
In real-life scenarios, ratios are commonly used to compare quantities in various contexts. For instance, in a recipe that requires 2 cups of flour and 1 cup of sugar, the ratio of flour to sugar is 2:1.
However, proportions come into play when we need to ensure balance and equivalence between different ratios. For example, if a recipe needs 4 cups of flour for every 2 cups of sugar, it forms a proportion where the ratios must be equal.
Difference between Ratio and Proportion
| Ratio | Proportion |
|---|---|
| Represents the relationship between two quantities | Represents the equality of two ratios |
| Can be simplified to its simplest form | Involves setting two ratios equal to each other |
| Expressed as a fraction or with a colon | Expressed as an equation with a proportion symbol |
| Does not necessarily involve equality | Always involves equality |
| Example: 2:3, 4/5, 6:9 | Example: 2:3 = 4:6, 3/4 = 6/8 |
Ratio and Proportion Formulas
Ratio Formula
Ratios are a way to compare quantities or amounts. The formula a: b can be interpreted as a divided by b.
Example: if you have 5 apples and 3 oranges, the ratio of apples to oranges is 5:3. This is expressed mathematically as 5/3.
Proportion Formula
Proportions express the equality of two ratios. The formula a : b :: c : d signifies that the first ratio is equal to the second ratio.
Example: if 2 pencils cost $1, then 4 pencils will cost $2, maintaining the proportion.
Ratio and Proportion Formula: Important Terms
In ratio and proportion formulas, certain terms play specific roles:
Ratio Formula Terms:
- Antecedent: Refers to the first term or quantity in a ratio or proportion. In 2:3, 2 is the antecedent.
- Consequent: Denotes the second term or quantity in a ratio or proportion. In 2:3, 3 is the consequent.
Proportion Formula Terms:
- Means: Represent the middle terms in a proportion. In a:b::c:d, both b and c are means.
- Extremes: Refer to the first and last terms in a proportion. In a:b::c:d, a and d are extremes.
Properties of Ratio and Proportion
Ratios and proportions have several important properties that come in handy when solving various mathematical problems. Here's a breakdown of some key properties:
Properties of Ratio
1. Inverse Ratio:
The inverse of a ratio a:b is b:a. It simply flips the order of the terms in the ratio. For example, the inverse of 2:3 (2 apples to 3 oranges) is 3:2 (3 oranges to 2 apples).
2. Adding or Subtracting Ratios (with a common denominator):
If two ratios have the same denominator (like parts being compared), you can add or subtract their numerators (values being compared) to get a new ratio. However, this only applies when the denominators are the same.
For example, if the ratio of boys to girls in a class is 3:2 and the ratio of teachers to students is 1:10, the combined ratio of boys and teachers to girls and students (assuming a common denominator of students) would be:
(3 + 1) : (2 + 10) = 4:12
3. Dividing Ratios (with a common numerator):
If two ratios have the same numerator (like the whole being compared), you can divide their denominators (parts being compared) to get a new ratio. Again, this applies only when the numerators are the same.
For example, if the ratio of flour to sugar in a cake recipe is 2:1 and the ratio of flour to butter is 2:3, the ratio of sugar to butter (assuming a common numerator of flour) would be:
1 : (3 / 2) = 1 : 1.5
4. Multiplying a Ratio by a Number:
You can multiply a ratio by a number to get a new ratio. This essentially scales the ratio proportionally. Multiplying by a number greater than 1 increases the ratio, and multiplying by a number between 0 and 1 (but not 0) decreases the ratio.
For example, if the ratio of red marbles to blue marbles in a bag is 2:3, multiplying it by 3 would result in a new ratio of 6:9 (both red and blue marbles increase proportionally).
Proportion Properties
Proportions exhibit distinct properties that help simplify mathematical relationships. These properties deal with manipulating proportions:
Extremes and Means: In a proportion a:b :: c:d, a and d are called the extremes, and b and c are called the means. You can multiply the means together or the extremes together to maintain the equality of the proportion.
For example, if 2:3 :: 8:12 is a proportion, then 2 x 12 (extremes multiplied) must be equal to 3 x 8 (means multiplied) which is true (24 = 24).
Here are other important properties:
- Addendo: If a : b = c : d, then a + c : b + d. This property states that you can add the corresponding terms (extremes or means) of a proportion to get another true proportion.
- Subtrahendo: If a : b = c : d, then a – c : b – d. Similar to addendo, you can subtract corresponding terms (extremes or means) to maintain a valid proportion.
- Dividendo: If a : b = c : d, then a – b : b = c – d : d. This property allows subtracting one term (mean) from another (mean) and dividing both by the remaining mean, resulting in a true proportion.
- Componendo: If a : b = c : d, then a + b : b = c+d : d. This property lets you add both terms (extremes or means) and divide by a common term (mean) to create another true proportion.
- Alternendo: If a : b = c : d, then a : c = b: d. This property allows swapping positions between the extremes and means while maintaining the equality of the proportion.
- Invertendo: If a : b = c : d, then b : a = d : c. You can invert the order of the terms within each ratio (a:b and c:d) to form another true proportion.
- Componendo and Dividendo (combined): If a : b = c : d, then a + b : a – b = c + d : c – d. This combines both componendo (adding terms and dividing by a mean) and dividendo (subtracting terms and dividing by a mean) into a single property.
How to Solve Ratio and Proportion Problems
Here are the steps to solve ratio and proportion problems:
- Read & Identify: Quickly grasp the problem and identify the quantities being compared and what needs to be solved for (often represented by a variable).
- Ratios as Fractions: Express the given information as ratios (colons or fractions) and simplify if possible.
- Set Up Proportion (if needed): If comparing ratios or finding a missing value, write a proportion using givens and the unknown.
- Solve (mostly cross-multiply):
- Cross-Multiplication: Multiply extremes (opposite corners) of the proportion and equate it to the product of means (terms next to each other).
- Unit Rates (if applicable): Use unit rates when dealing with rates and time.
- Ratio Properties (less common): In specific cases, use properties like adding/subtracting ratios with a common denominator.
- Solve & Verify: Solve the equation (usually from cross-multiplication) and check the answer in the context of the problem.
Ratio and Proportion Tricks
When faced with a problem, distinguish between when to use ratios and when to use proportions. Ratios compare two quantities directly, while proportions involve an equality between two ratios. Look for keywords like "per," "for every," or "is to" to identify when proportions are needed.
Shortcuts can be handy when tackling ratio and proportion problems. One such shortcut is the "Cross-Multiplication Method," where you multiply the extremes and means of two ratios to find the unknown quantity quickly.
Ratio and Proportion Examples With Answers
Here's an example to illustrate these steps:
Problem: A recipe requires a ratio of 2 cups flour to 3 eggs. If you have 6 eggs, how many cups of flour do you need?
Solution:
- Understand: We need to find the number of cups of flour (unknown) for 6 eggs (given).
- Represent Ratios: Flour to eggs ratio = 2:3 (given).
- Identify Missing Value: We need to find the number of cups of flour (represented by x).
- Set Up a Proportion: Since we have a ratio and need to find a missing value, we can write a proportion: 2:3 :: x:6 (flour:eggs :: unknown flour:6 eggs).
- Solve (Cross-Multiplication): Multiply extremes (2 x 6) and equate it to the product of means (3 x). This gives 12 = 3x. Solve for x by dividing both sides by 3: x = 4.
- Verify: For 6 eggs, we need 4 cups of flour. This makes sense based on the original ratio.
Ratio and Proportion Problems (With Solutions)
Q1. If the ratio of boys to girls in a class is 3:2 and there are 14 girls, how many boys are there?
Options:
a) 21
b) 18
c) 20
d) 24
Answer: a) 21
Solution Explained:
Here's how to find the number of boys in the class:
- Total parts of the ratio: 3+2 = 5.
- Girls represent 2 parts of the total, i.e. the number of students. If we take the total number of students to be x then: (2/5)*x=14.
- Solving for x: x= (14*5)/2
- x=70/2=35
- Number of boys will be the number of girls subtracted from the total number of students:
- 35-14 = 21
- Therefore, there are 21 boys in the class.
Alternate Solution:
- We know 3:2 is the ratio of students in the class. If we take the students in class to be x:
- The number of girl students 2x is equal to 14. Solving for x: 2x=14 OR x = 7.
- The number of boy students: 3x = 3*7 = 21.
Q2. If 4 apples cost INR 200, what is the cost of 6 apples?
Options:
a) INR 350
b) INR 250
c) INR 300
d) INR 400
Answer: c) INR 300
Solution Explained:
Here’s how to solve this:
- Cost of 4 apples: 200
- Cost of 1 apple=200/4 OR 50
- Cost of 6 apples= (200/4)*6 OR 50*6 =300
- Thus, the cost of 6 apples is INR 300.
Q3. If the ratio of the sides of two similar triangles is 3:4, and the perimeter of the smaller triangle is 15, what is the perimeter of the larger triangle?
Options:
a) 18
b) 21
c) 24
d) 20
Answer: d) 20
Solution Explained:
Here’s how to solve this:
- Identify what we know:
- Ratio of sides of similar triangles = 3:4
- Perimeter of smaller triangle = 15 (Perimeter is the sum of all sides)
- Understand the connection:
- Since the triangles are similar, the ratio of their corresponding sides is the same as the ratio of their perimeters.
- Let x be the perimeter of the larger triangle.
- Set up a proportion:
- Perimeter of smaller triangle : Perimeter of larger triangle = Ratio of sides of smaller triangle: Ratio of sides of larger triangle
- 15 : x = 3 : 4
- Solve (cross-multiply):
- Multiply extremes (15 and 4): 15 x 4 = x x 3
- Solve for x: x = (15 x 4) / 3 = 20
- The perimeter of the lower triangle is 20.
Q4. If 8 pens cost INR120, what is the cost of 6 pens?
Options:
a) INR 80
b) INR 100
c) INR 110
d) INR 90
Answer: d) INR 90
Solution Explained:
Here’s how to solve this:
- Cost of 8 pens: 120
- Cost of 1 pen=120/8 OR 15
- Cost of 6 pens= (120/8)*6 OR 15*6 =90
- Thus, the cost of 6 pens is INR 90.
Q5. If the ratio of the ages of two persons is 2:3 and the older person is 30 years old, how old is the younger person?
Options:
a) 25 years
b) 28 years
c) 32 years
d) 20 years
Answer: d) 20 years
Solution Explained:
Here’s how to solve this
- We know 2:3 is the ratio of ages. If we take age to be x:
- Age of older person: 3x is equal to 30. Solving for x: 3x=30 OR x = 10.
- Age of younger person: 2x = 2*10 = 20.
Q6. In a mixture of milk and water, the ratio of milk to water is 5:2. If the mixture contains 21 liters of water, how many liters of milk are there?
Options:
a) 30 liters
b) 35 liters
c) 40 liters
d) 52.5 liters
Answer: d) 52.5 liters
Solution Explained:
Here’s how to solve this
- We know 5:2 is the ratio of milk to water in the mixture. If we take the mixture to be x:
- Liters of water in the mixture, 2x is equal to 21. Solving for x: 2x=21 OR x = 10.5.
- Liters of mik in the mixture, 5x = 5*10.5 = 52.5.
- Thus, the mixture contains 52.5 liters of milk.
Q7. If 18 books cost INR 540, how many books can be bought for INR 900?
Options:
a) 20
b) 25
c) 30
d) 35
Answer: c) 30
Solution Explained:
Here’s how to solve this:
- Cost of 18 books: 540
- Cost of 1 book=540/18 OR 30
- Books that can be bought for INR 900= 900/30=30
- Thus, 30 books can be bought for INR 900.
Q8. If the ratio of the areas of two squares is 4:9, what is the ratio of their perimeters?
Options:
a) 3:4
b) 1:2
c) 1:3
d) 2:3
Answer: d) 2:3
Solution Explained:
While the areas of squares are related to the square of their side lengths, the perimeter is directly proportional to the side length itself. Here's how to find the ratio of perimeters:
- Understand the connection: Area of a square = side length ^ 2 (s^2), Perimeter of a square = 4 * side length (4s).
- Recognize the key point: The ratio of areas is given (4:9), but we need the ratio of perimeters.
- Focus on side lengths: Since area is proportional to the square of the side length, a ratio of areas 4:9 implies a ratio of the side lengths of the squares as 2:3 (square root of 4 is 2 and square root of 9 is 3).
- Relate to perimeters: If the side length ratio is 2:3, the perimeters will also be in the same ratio because the perimeter is directly proportional to the side length (4 times the side length for a square).
- Therefore, the ratio of the perimeters of the two squares is 2:3.
Q9. If the ratio of the present ages of Jack and Jill is 4:5 and that of Jill and Jane is 7:8, what is the ratio of Jack's age to Jane's age?
Options:
a) 20:33
b) 12:29
c) 7:10
d) 16:35
Answer: c) 7:10
Solution Explained:
- The common factor in both ratios is Jill’s age. We will convert Jack and Jane’s age in terms of Jill’s each to arrive at the final solution:
- Let’s consider Jill’s age = x for ease of calculation
- Take the ratio of Jack and Jill’s age (4:5) and cross-multiple to solve Jack’s age in terms of Jill’s age: Jack’s age = (5/4)x
- Take the ratio of Jill and Jane’s age (7:8) and cross-multiple to solve Jane’s age in terms of Jill’s age: Jane’s age = (7/8)x
- The ratio of Jack to Jane’s age: (5/4)x/(7/8)x = 35/40 (x gets cancelled out)
- Simplifying the fraction further gives the final ratio of Jack to Jane’s age as 7:10.
Q10. If the ratio of the volumes of two spheres is 8:27, what is the ratio of their surface areas?
Options:
a) 3:8
b) 2:7
c) 5:12
d) 4:9
Answer: d) 4:9
Solution Explained:
Here’s how to solve this:
- The ratio of the volumes of two spheres is given as 8:27.
- We know that the volume (V) of a sphere is proportional to the cube of its radius (r). So, if the ratio of volumes is 8:278:27, the ratio of their radii (r) will be ∛8:∛27.
- Ratio of radii: ∛8:∛27=2/3:3/3=2:3
- Now, the surface area (A) of a sphere is proportional to the square of its radius (r). So, if the ratio of the radii is 2:3, the ratio of their surface areas will be (2^2):(3^2).
- Ratio of surface areas=4:9
- Therefore, the ratio of the surface areas of the two spheres is 4:9
Q11. In a mixture of milk and water, the ratio of milk to water is 5:3. If 10 liters of water is added to the mixture, the ratio becomes 5:4. What is the quantity of milk in the mixture before adding water?
Options:
a) 50 liters
b) 30 liters
c) 15 liters
d) 25 liters
Answer: a) 50 liters
Solution Explained:
Here’s how to solve this:
- We know 5:3 is the ratio of milk to water in the mixture. If we take the mixture to be x:
- Liters of water in the mixture, 3x and Liters of mik in the mixture.
- New ratio after the addition of 10 liters of milk: 5x/(3x+10) = 5/4
- Solving for x through cross-multiplication:
- 5x*4 = 5*(3x+10)
- 20x=15x+50
- 20x-15x= 50 OR 5x = 50
- x=10
- Now the original quantity of water in the mixture = 5x. If x= 10, then the quantity of milk = 50 liters
- Thus, the mixture contains 50 liters of milk.
Q12. A sum of money is to be divided among A, B, and C in the ratio 2:3:5. If the difference between the shares of A and B is INR 400, what is C's share?
Options:
a) INR 1,500
b) INR 800
c) INR 1,200
d) INR 2,000
Answer: d) INR 2,000
Solution Explained:
Here’s how to solve this:
- We know the money is divided between A:B:C as 2:3:5. If we take the sum of money to be x:
- A’s share: 2x; B’s share: 3x; C’s share: 5x
- The difference in B and A’s share = 400. Solving for x:
- 3x-2x = 400 OR x = 400
- Calculating C’s share: 5*400 = 2000
- C’s share is INR 2,000.
Enhance your knowledge of ratio and proportion with the Quantitative Aptitude course on Unstop.
Summary
You've now gained a solid understanding of mathematical ratios and proportions, distinguishing between the two, learning their formulas, exploring real-world applications, understanding properties and types, and receiving tips for mastering them. By applying these concepts in various scenarios, you can enhance your problem-solving skills and analytical thinking.
Remember to practice solving ratio and proportion problems regularly to reinforce your comprehension and boost your math proficiency.
Time For A Short Quiz
Frequently Asked Questions
1. What is the difference between a ratio and a proportion?
A ratio compares two quantities, while a proportion states that two ratios are equal. Ratios show relationships between numbers, whereas proportions involve setting up equivalent fractions to solve for an unknown value.
2. Are there specific formulas to calculate ratios and proportions?
Yes, for ratios, you divide one quantity by another. Proportions involve setting up equal fractions. The cross-multiplication method is commonly used to solve proportion problems efficiently.
3. What is a ratio?
A ratio is a comparison of two quantities by division. It expresses the relative size of two quantities, typically represented as a/b, where a and b are two numbers.
4. How do you simplify a ratio?
To simplify a ratio, divide both parts of the ratio by their greatest common divisor (GCD). This ensures that the ratio is in its simplest form.
5. What is a proportion?
A proportion is an equation stating that two ratios are equal. It can be represented as a/b=c/d, where a, b, c, and d are numbers.
6. How do you solve proportion problems?
To solve proportion problems, you can use cross multiplication. This involves multiplying the extremes (the first and last terms) and the means (the second and third terms) of the proportion and setting the products equal to each other.
7. What are some real-life applications of ratios and proportions?
Ratios and proportions are widely used in various real-life scenarios such as cooking recipes (e.g., ingredient ratios), financial planning (e.g., calculating interest rates), scaling (e.g., enlarging or reducing maps or blueprints), and in geometry (e.g., finding similar shapes).
Suggested Reads:
- Average in Maths: Definition, Symbol, Formula & Solved Questions)
- Angle Of Elevation: Formula With Practice Questions & Answers
- HCF And LCM Methods: Formula, Practice Questions And Answers
- Decimal Fraction: Find Types, Operations & Practice Questions
- Height And Distance- Trigonometry Basics With Question & Answer
I’m a reader first and a writer second, constantly diving into the world of content. If I’m not writing or reading, I like watching movies and dreaming of a life by the beach.
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter
















Comments
Add comment