- Step 1: The Groundwork
- Step 2: The Three Sections
- Step 3: Practice Makes Improvement
- The Secret Ingredient
- Understanding Basics Of Number Series
- Types Of Number Series Reasoning Questions
- Addition & Multiplication In Number Series
- Square & Cube-Based Number Series Patterns
- Missing Terms & Arranging Sequences
- Tricks & Tips For Solving Number Series
- Selected Number Series Questions With Solutions
- Frequently Asked Questions (FAQs)
- Must Know Terminologies in Blood Relation Questions
- Basic Approaches to Solve Blood Relation Questions
- Types Of Blood Relation Questions
- Tips For Solving Blood Relation Questions
- Multiple Choice Questions (MCQs) with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Letter Series In Logical Reasoning
- Types Of Letter Series Patterns
- Tips For Solving Letter Series Reasoning
- Best Practice Question Samples With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basics of Problems On Age-Related Questions
- Formula to Solve Problems on Ages-Related Questions
- Types of Age-Related Questions & Examples
- Tips & Tricks for Solving Ages Problems
- Best MCQs on Problems on ages with solved answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition of Calendar
- Understanding Days of the Week
- What is a Leap Year?
- Concept of Odd Days in a Century
- Tips For Solving Calendar Reasoning Questions
- Best Calendar Reasoning Questions with Answers (MCQs)
- Frequently Asked Questions (FAQs)
- Basic Concepts of Clock
- Structure of a Clock
- Angle Equilavalence in Clock
- Tips For Solving Clock Questions
- Selected Clock Questions & Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding The Concept Of Direction Sense
- Tips For Effective Problem-Solving In Direction Sense
- Practical Test Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Dice Reasoning
- Dice Numbers In Dice Reasoning
- Classification Of Dice
- Constructed Vs Deconstructed Dice
- Tricks & Tips For Solving Dice Problems
- Practice MCQs With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Alphanumeric Series Defined
- Alphanumeric Series In Reasoning Tests
- Tips & Strategies For Solving Alphanumeric Series
- Practice Sample Questions With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept Of Mirror Image Reasoning Explained
- Important Terms In Mirror Image Reasoning
- Types Of Mirror Images
- Identifying Correct Mirror Image
- Finding Clock's Mirror Image
- Tips To Solve Mirror Images
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept & Overview Of Input-Output
- Input-Output In Competitive Exams
- Types Of Input-Output Problems
- Strategies, Tips & Tricks For Solving Reasoning Questions
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Finding The Odd One Out
- Tricks And Tips
- How to Find The Odd One Out?
- Solved MCQs with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Key Concepts
- Exploring Different Ranking Types
- Formula And Application Of Order And Ranking
- Tips For Solving Order & Ranking
- Selected Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Pipes & Cistern Aptitude
- Key Terminologies used in Pipes and Cisterns
- Pipes and Cisterns Formula with Examples
- Pipes and Cisterns Shortcut Tricks
- Tips For Solving Pipes & Cistern Problems
- Selected Questions & Answers For Practice (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Key Concept in Boats and Streams
- Formulas Of Boats & Streams
- Distance & Time Formula
- Tips For Solving Boats & Streams Questions
- Selected Practice Questions With Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept of Mixture and Alligation
- Types Of Alligation Questions
- Formula for Solving Mixture & Alligation
- Tips For Solving Mixture And Alligation
- Selected Questions With Answers For Practice
- Conclusion
- Frequently Asked Questions (FAQs)
- Concepts and Definitions Related to Time and Work
- Important Time And Work Formulas
- Tricks and Tips to Solve Time & Work Questions
- Time And Work MCQs with Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Harmonic Progression(HP)?
- Formula to find the nth Term in Harmonic Progression
- Formula to find the Sum of the nth Term in HP
- What is Harmonic Mean?
- Harmonic Progression Solved Best MCQs
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Mensuration in Maths?
- What are 2D figures in Mensuration?
- What are 3D figures in Mensuartion?
- Basic Terminologies In Mensuration
- Basic 2D Formulas in Mensuration
- Basic 3D Formulas in Mensuration
- 2D vs 3D in Mensuration
- Solved Questions With Solutions (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Relationship Between Time, Speed And Distance
- Conversion Units Time, Speed And Distance
- Average & Relative Speed: Two Trains Moving in the same or opposite direction
- Solved MCQs on Time, Speed And Distance
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Simplification in Maths?
- BODMAS Rule in Simplification Explained
- Simplification & Approximation Relation
- Key Terms in Simplification
- Examples Of Simplification Techniques
- Simplification Questions With Solved Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Height And Distance Important Terms
- Right Angled Triangle In Trigonometry
- Trigonometric Ratios
- Solved Examples For Better Understanding
- Height And Distance Applications In Trigonometry
- Height And Distance Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Interest Types
- Simple Interest Vs. Compound Interest
- Selected Solved Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basic Concepts Of Profit And Loss
- Determining Selling Price
- Calculating Discounts
- Formulas For Calculating Profit And Loss
- Examples Of Profit And Loss
- Profit & Loss Questions With Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Angle Of Elevation
- Key Terms Used In Angle Of Elevation
- Angle of Elevation Formula with Example
- Angle of Elevation vs. Angle of Depression
- Angle of Elevation MCQs with Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining HCF And LCM
- Calculation Methods Of HCF And LCM
- HCF By Prime Factorization Method
- LCM By Prime Factorization Method
- Difference Between HCF And LCM
- HCF & LCM Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- What is fraction and decimal?
- Understanding Decimal Fraction
- Place Value in Decimal Fraction
- Mathematical Operations with Decimal Fraction
- Practice with Solved Examples
- Summary
- Frequently Asked Questions
- All About Decimals
- All About Fractions
- How to Convert a Decimal into Fraction
- Simple vs Recurring Decimals
- Converting Recurring Decimals to Fractions
- Conversion Charts
- Practice Questions (With Solutions)
- Closing Thoughts
- Frequently Asked Questions
- What is Arithmetic Mean?
- Arithmetic Mean Formula- Ungroup Data & Group Data
- Merits of Arithmetic Mean
- Demerits of Arithmetic Mean
- Alternatives to Arithmetic Mean
- What is the Weighted Arithmetic Mean?
- Arithmetic vs. Geometric Mean
- Arithmetic Mean Application in Statistical Analysis
- Arithmetic Mean Practice Questions with Explanation
- Frequently Asked Questions
- What is Geometric Progression?
- Key Properties of Geometric Progression
- General Form Of Geometric Progression
- General Term or the Nth Term of Geometric Progression
- The sum of nth Terms of GP
- Types Of Geometric Progression
- Solved Questions and Answers of GP
- Conclusion
- Frequently Asked Questions (FAQs)
- Average in Maths
- Average Formula in Maths
- Differentiating Types of Average
- How to Calculate Average of Negative Numbers?
- Practical Applications of Averages
- Average Questions For Practice
- Frequently Asked Questions
- What is Simple Interest in Maths?
- Simple Interest Formula Explained
- Simple Interest Formula for Years, Months & Days
- Simple Interest Examples & Practice Questions
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Mathematical Ratios
- Understanding Proportions Fundamentals
- Differentiating Ratios from Proportions
- Ratio and Proportion Formulas
- Properties of Ratio and Proportion
- How to Solve Ratio and Proportion Problems
- Ratio and Proportion Problems (With Solutions)
- Summary
- Frequently Asked Questions
- What is Number in Maths?
- Types of Numbers With Example
- Real vs Complex Numbers Explored
- Basic Operations on Numbers
- Practice Questions (With Solutions)
- Frequently Asked Questions
- What is Arithmetic Progression (AP) in Maths?
- Important Terminologies in Arithmetic Progression
- Basic Terms in Arithmetic Progression
- General Form Of Arithmetic Progression Series
- Types Of Arithmetic Progression
- Solved Questions With Explanation (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Basic Concept
- Importance Of Train Problems In Aptitude
- Tips To Solve Train Problems
- Selected Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition Of Mode
- Calculating Mode For Ungrouped Data
- Calculating Mode For Grouped Data
- Bimodal, Trimodal & Multimodal Distributions
- Comparing Mean, Median & Mode
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Important Concept In Races And Games
- Calculating Time, Speed & Distance
- Importance Of Races And Games Problems
- Sample Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Types Of Partnership
- Formula For Partnership Questions
- Tips To Solve Partnership Aptitude Questions
- Selected Partnership Questions (Practice MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
Simplification: BODMAS Rule, Formulas, Techniques, and Solved MCQs

Students can better understand the underlying principles and relationships by simplifying mathematical expressions, equations, and concepts. This process not only enhances problem-solving skills but also promotes critical thinking and analytical reasoning.
What is Simplification in Maths?
Simplification in mathematics involves reducing complex expressions to their simplest form by combining like terms or eliminating unnecessary elements. Simplifying equations and expressions makes them easier to work with, understand, and manipulate.

BODMAS Rule in Simplification Explained
Let us study the role of BODMAS in simplification:

Order Of Operations
BODMAS, which stands for Brackets, Of, Division, Multiplication, Addition, and Subtraction, is a fundamental mathematical rule to ensure accurate calculations. The order of operations dictates the sequence in which mathematical operations should be performed.
First, calculations within brackets are solved, followed by any exponents or roots. Then, division and multiplication are carried out from left to right before finally adding and subtracting similarly from left to right.
Vinculum In Mathematics
The vinculum, a horizontal line in mathematical expressions, is crucial in simplification. It often indicates the grouping of numbers or terms within an expression, indicating which operations should be performed first.
Click here to enhance and upskill your quantitative aptitude related to simplification right away!
Simplification & Approximation Relation
Simplification involves reducing a mathematical expression to its simplest form, while approximation focuses on finding close or near values to the actual result. When simplifying, exact values are sought after, whereas in approximation, approximate values are acceptable.
When doing math, simplification gives exact answers without rounding. Approximation is better for quick and efficient calculations when decimals work fine. In real-world applications like data analysis or statistics, approximation is often preferred over exact simplification due to time constraints and practicality.
Key Terms in Simplification
Let us study some of the key terms used in simplification:
Key Term |
Definition |
|---|---|
| Factors | Numbers multiplied together to produce a different number are called factors. |
| Multiples | The result of multiplying a number by an integer |
| Common Denominators | Shared values in fractions that allow for easy addition or subtraction |
| Expression | Mathematical phrases containing numbers, variables, and operations like addition or multiplication |
| Roots | Solutions or values that make the expression equal to zero |
| Base | The number is raised to a power in exponential expressions |
| Type | Different types of mathematical operations, such as addition, subtraction, multiplication, and division |
| Place Value | The value of a digit based on its position in a number |
| Order of Operations | A sequence in which mathematical operations should be performed to simplify expressions accurately |
| Fraction | A fraction consists of a numerator (the top number) and a denominator (the bottom number) |
| Exponent | An exponent is a small number above and to the right of a base number. It shows how many times the base number should be multiplied by itself. |
Examples Of Simplification Techniques
Let us study some of the examples of simplification:
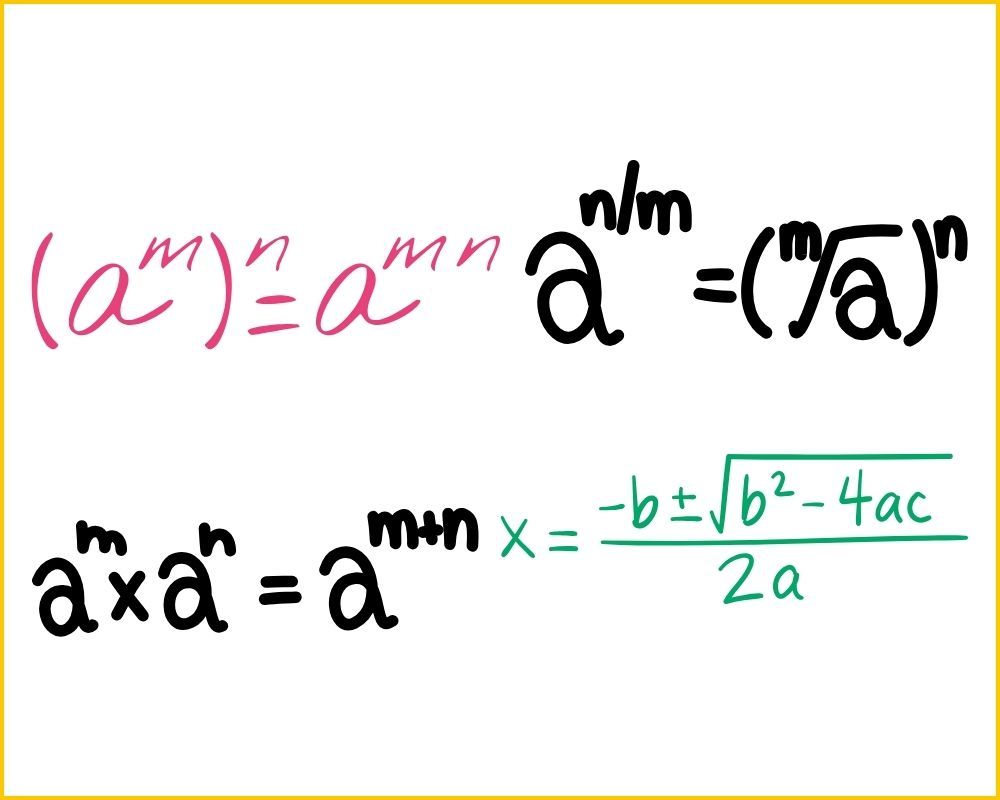
Fractions: Simplifying fractions means making them simpler by dividing the top and bottom numbers by their biggest shared number.
Exponents: When simplifying expressions with exponents, apply the rule that states when you divide two terms with the same base, subtract the exponents.
Algebraic Expressions: In algebra, simplification often involves combining like terms and performing operations following the order of operations.
Simplification Questions With Solved Answers (MCQs)
For your practice, we have selected some questions with detailed answers. Practice them and get ready for any placement interview or competitive exams:
Question 1. Find the value of (3 * 4) – (8 + 12).
(a) 9
(b) 9.25
(c) –9.25
(d) None of these
Solution b) 9.25
Explanation: Let us apply the BODMAS rule to solve this question,
(3 * 4) – (8 + 12) = –37 – (–4). [Note here that the ‘–’ sign between –37 and –4 is the operation defined above.]
= 37/4 = 9.25
(Define the following functions for the questions (2 - 4):
(a) (a M b) = a – b
(b) (a D b) = a + b
(c) (a H b) = ab
(d) (a P b) = a/b)
Question 2. What is the value of (3M4H2D4P8M2)? Define the following functions:
(a) 6.5
(b) 6
(c) –6.5
(d) None of these
Solution: c) -6.5
Explanation: 3– 4 x 2 + 4/8 – 2 = 3 – 8 + 0.5 – 2 = – 6.5
Question 3. Which of the following functions will represent a2 – b2?
(a) (a M b) H (a D b)
(b) (a H b) M (a P b)
(c) (a D b)/(a M b)
(d) None of these
Solution: a) (a M b) H (a D b)
Explanation: Solve using the options
option a = (a – b) (a + b) = a2 – b2.
Question 4. Which of the following represents a2?
(a) (a M b) H (a D b) + b2
(b) (a H b) M (a P b) + b2
(c) (a M b)/(a P b)
(d) Both (a) and (c)
Solution: a) (a M b) H (a D b) + b2
Explanation: Solve using the options
Option a = (a2 – b2 ) + b2 = a2
Question 5. If 381A is divisible by 9, find the value of the smallest natural number A.
(a) 5
(b) 4
(c) 7
(d) 6
Solution: d) 6
Explanation: For the given number 381A to be divisible by 9, its sum 3 + 8 + 1 + A should be divisible by 9. Choosing from among the giving options, A should be 6. Option (d) is correct.
Question 6. What will be the remainder obtained when (96 + 1) will be divided by 8?
(a) 0
(b) 3
(c) 7
(d) 2
Solution: d) 2
Explanation: 96, when divided by 8, would give a remainder of 1. Hence, the required answer would be 2.
Question 7. Determine the ratio between the LCM and HCF of 5, 15, and 20 is
(a) 8:1
(b) 14:3
(c) 12:2
(d) 12:1
Solution: d) 12:1
Explanation: Given 5, 15 and 20. The LCM of these numbers is 60.
Likewise, 5 is the HCF of 5, 15 and 20.
Therefore, the ratio is 60:5 = 12:1
Question 8. Find the LCM of 5/2, 8/9, 11/14.
(a) 280
(b) 360
(c) 420
(d) None of these
Solution: d) None of these
Here's a step-by-step explanation:
LCM of 5/2, 8/9 and 11/14 would be given by: (LCM of numerators)/(HCF of denominators) = 440/1 = 44.
Question 9. A five-digit number is taken. The sum of the first four digits (excluding the number at the unit digit) equals the sum of all five digits. Which of the following will not necessarily divide this number?
(a) 10
(b) 2
(c) 4
(d) 5
Solution: c) 4
Explanation: The essence of this question is in the fact that the last digit of the number is 0.
Naturally, the number is necessarily divisible by 2,5 and 10. Only 4 does not necessarily divide it.
Question 10. Find the number of divisors of 1420.
(a) 14
(b) 15
(c) 13
(d) 12
Solution: d) 12
Explanation: 1420 = 142 x 10 = 22 x 711 x 51.
The total factors of the number can be calculated by adding 1 to each exponent in the prime factorization and then multiplying them together as (2+1) x (1+1) x (1+1) = 3 x 2 x 2 = 12. Option (d) is correct.
Conclusion
The exploration of simplification techniques has provided a comprehensive understanding of the fundamental principles of solving mathematical problems efficiently. From grasping the basics to mastering advanced strategies, the journey through BODMAS rules, vinculum applications, and approximation relations has equipped individuals with the tools to simplify complex calculations effectively.
To further enhance mathematical proficiency, individuals are encouraged to practice regularly, seek challenging problems for application, and remain diligent in honing their simplification skills.
Time For A Short Quiz
Frequently Asked Questions (FAQs)
1. What are the key principles of simplification in mathematics?
Simplification in mathematics involves applying basic rules like BODMAS, understanding the vinculum, and using approximation techniques to solve complex problems efficiently.
2. How can one effectively master the art of simplification in mathematics?
To master simplification, one should practice regularly, understand key terms, use strategies like BODMAS, learn various techniques through examples, and focus on precision while approximating values.
3. Can you explain the significance of the BODMAS rule in simplification?
The BODMAS rule (Brackets, Orders, Division/Multiplication, Addition/Subtraction) is crucial for maintaining the correct order of operations when simplifying mathematical expressions to ensure accurate results.
4. What role do approximation techniques play in simplification?
Approximation techniques help simplify complex calculations by replacing numbers with easier values while ensuring the result is close enough to the actual value for practical purposes.
5. How do strategies like breaking down problems aid in effective simplification?
Breaking down problems into smaller steps or components allows individuals to handle each part systematically, making it easier to simplify complex expressions and arrive at accurate solutions efficiently.
Suggested reads:
- What Is Mensuration: Formulas With Top Selected Question & Answer
- Harmonic Progression- Formula With Selected Questions & Answers
- Mixture And Alligation: Explained With Selected Question & Answer
- Boats And Streams: Formula, Top Question With Solution (Aptitude)
- Clock Questions: Selected Question & Answer (Aptitude) Explained
Instinctively, I fall for nature, music, humor, reading, writing, listening, traveling, observing, learning, unlearning, friendship, exercise, etc., all these from the cradle to the grave- that's ME! It's my irrefutable belief in the uniqueness of all. I'll vehemently defend your right to be your best while I expect the same from you!
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter















Comments
Add comment