- Step 1: The Groundwork
- Step 2: The Three Sections
- Step 3: Practice Makes Improvement
- The Secret Ingredient
- Understanding Basics Of Number Series
- Types Of Number Series Reasoning Questions
- Addition & Multiplication In Number Series
- Square & Cube-Based Number Series Patterns
- Missing Terms & Arranging Sequences
- Tricks & Tips For Solving Number Series
- Selected Number Series Questions With Solutions
- Frequently Asked Questions (FAQs)
- Must Know Terminologies in Blood Relation Questions
- Basic Approaches to Solve Blood Relation Questions
- Types Of Blood Relation Questions
- Tips For Solving Blood Relation Questions
- Multiple Choice Questions (MCQs) with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Letter Series In Logical Reasoning
- Types Of Letter Series Patterns
- Tips For Solving Letter Series Reasoning
- Best Practice Question Samples With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basics of Problems On Age-Related Questions
- Formula to Solve Problems on Ages-Related Questions
- Types of Age-Related Questions & Examples
- Tips & Tricks for Solving Ages Problems
- Best MCQs on Problems on ages with solved answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition of Calendar
- Understanding Days of the Week
- What is a Leap Year?
- Concept of Odd Days in a Century
- Tips For Solving Calendar Reasoning Questions
- Best Calendar Reasoning Questions with Answers (MCQs)
- Frequently Asked Questions (FAQs)
- Basic Concepts of Clock
- Structure of a Clock
- Angle Equilavalence in Clock
- Tips For Solving Clock Questions
- Selected Clock Questions & Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding The Concept Of Direction Sense
- Tips For Effective Problem-Solving In Direction Sense
- Practical Test Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Dice Reasoning
- Dice Numbers In Dice Reasoning
- Classification Of Dice
- Constructed Vs Deconstructed Dice
- Tricks & Tips For Solving Dice Problems
- Practice MCQs With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Alphanumeric Series Defined
- Alphanumeric Series In Reasoning Tests
- Tips & Strategies For Solving Alphanumeric Series
- Practice Sample Questions With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept Of Mirror Image Reasoning Explained
- Important Terms In Mirror Image Reasoning
- Types Of Mirror Images
- Identifying Correct Mirror Image
- Finding Clock's Mirror Image
- Tips To Solve Mirror Images
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept & Overview Of Input-Output
- Input-Output In Competitive Exams
- Types Of Input-Output Problems
- Strategies, Tips & Tricks For Solving Reasoning Questions
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Finding The Odd One Out
- Tricks And Tips
- How to Find The Odd One Out?
- Solved MCQs with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Key Concepts
- Exploring Different Ranking Types
- Formula And Application Of Order And Ranking
- Tips For Solving Order & Ranking
- Selected Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Pipes & Cistern Aptitude
- Key Terminologies used in Pipes and Cisterns
- Pipes and Cisterns Formula with Examples
- Pipes and Cisterns Shortcut Tricks
- Tips For Solving Pipes & Cistern Problems
- Selected Questions & Answers For Practice (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Key Concept in Boats and Streams
- Formulas Of Boats & Streams
- Distance & Time Formula
- Tips For Solving Boats & Streams Questions
- Selected Practice Questions With Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept of Mixture and Alligation
- Types Of Alligation Questions
- Formula for Solving Mixture & Alligation
- Tips For Solving Mixture And Alligation
- Selected Questions With Answers For Practice
- Conclusion
- Frequently Asked Questions (FAQs)
- Concepts and Definitions Related to Time and Work
- Important Time And Work Formulas
- Tricks and Tips to Solve Time & Work Questions
- Time And Work MCQs with Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Harmonic Progression(HP)?
- Formula to find the nth Term in Harmonic Progression
- Formula to find the Sum of the nth Term in HP
- What is Harmonic Mean?
- Harmonic Progression Solved Best MCQs
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Mensuration in Maths?
- What are 2D figures in Mensuration?
- What are 3D figures in Mensuartion?
- Basic Terminologies In Mensuration
- Basic 2D Formulas in Mensuration
- Basic 3D Formulas in Mensuration
- 2D vs 3D in Mensuration
- Solved Questions With Solutions (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Relationship Between Time, Speed And Distance
- Conversion Units Time, Speed And Distance
- Average & Relative Speed: Two Trains Moving in the same or opposite direction
- Solved MCQs on Time, Speed And Distance
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Simplification in Maths?
- BODMAS Rule in Simplification Explained
- Simplification & Approximation Relation
- Key Terms in Simplification
- Examples Of Simplification Techniques
- Simplification Questions With Solved Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Height And Distance Important Terms
- Right Angled Triangle In Trigonometry
- Trigonometric Ratios
- Solved Examples For Better Understanding
- Height And Distance Applications In Trigonometry
- Height And Distance Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Interest Types
- Simple Interest Vs. Compound Interest
- Selected Solved Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basic Concepts Of Profit And Loss
- Determining Selling Price
- Calculating Discounts
- Formulas For Calculating Profit And Loss
- Examples Of Profit And Loss
- Profit & Loss Questions With Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Angle Of Elevation
- Key Terms Used In Angle Of Elevation
- Angle of Elevation Formula with Example
- Angle of Elevation vs. Angle of Depression
- Angle of Elevation MCQs with Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining HCF And LCM
- Calculation Methods Of HCF And LCM
- HCF By Prime Factorization Method
- LCM By Prime Factorization Method
- Difference Between HCF And LCM
- HCF & LCM Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- What is fraction and decimal?
- Understanding Decimal Fraction
- Place Value in Decimal Fraction
- Mathematical Operations with Decimal Fraction
- Practice with Solved Examples
- Summary
- Frequently Asked Questions
- All About Decimals
- All About Fractions
- How to Convert a Decimal into Fraction
- Simple vs Recurring Decimals
- Converting Recurring Decimals to Fractions
- Conversion Charts
- Practice Questions (With Solutions)
- Closing Thoughts
- Frequently Asked Questions
- What is Arithmetic Mean?
- Arithmetic Mean Formula- Ungroup Data & Group Data
- Merits of Arithmetic Mean
- Demerits of Arithmetic Mean
- Alternatives to Arithmetic Mean
- What is the Weighted Arithmetic Mean?
- Arithmetic vs. Geometric Mean
- Arithmetic Mean Application in Statistical Analysis
- Arithmetic Mean Practice Questions with Explanation
- Frequently Asked Questions
- What is Geometric Progression?
- Key Properties of Geometric Progression
- General Form Of Geometric Progression
- General Term or the Nth Term of Geometric Progression
- The sum of nth Terms of GP
- Types Of Geometric Progression
- Solved Questions and Answers of GP
- Conclusion
- Frequently Asked Questions (FAQs)
- Average in Maths
- Average Formula in Maths
- Differentiating Types of Average
- How to Calculate Average of Negative Numbers?
- Practical Applications of Averages
- Average Questions For Practice
- Frequently Asked Questions
- What is Simple Interest in Maths?
- Simple Interest Formula Explained
- Simple Interest Formula for Years, Months & Days
- Simple Interest Examples & Practice Questions
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Mathematical Ratios
- Understanding Proportions Fundamentals
- Differentiating Ratios from Proportions
- Ratio and Proportion Formulas
- Properties of Ratio and Proportion
- How to Solve Ratio and Proportion Problems
- Ratio and Proportion Problems (With Solutions)
- Summary
- Frequently Asked Questions
- What is Number in Maths?
- Types of Numbers With Example
- Real vs Complex Numbers Explored
- Basic Operations on Numbers
- Practice Questions (With Solutions)
- Frequently Asked Questions
- What is Arithmetic Progression (AP) in Maths?
- Important Terminologies in Arithmetic Progression
- Basic Terms in Arithmetic Progression
- General Form Of Arithmetic Progression Series
- Types Of Arithmetic Progression
- Solved Questions With Explanation (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Basic Concept
- Importance Of Train Problems In Aptitude
- Tips To Solve Train Problems
- Selected Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition Of Mode
- Calculating Mode For Ungrouped Data
- Calculating Mode For Grouped Data
- Bimodal, Trimodal & Multimodal Distributions
- Comparing Mean, Median & Mode
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Important Concept In Races And Games
- Calculating Time, Speed & Distance
- Importance Of Races And Games Problems
- Sample Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Types Of Partnership
- Formula For Partnership Questions
- Tips To Solve Partnership Aptitude Questions
- Selected Partnership Questions (Practice MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
Angle Of Elevation: Definition, Formula, Questions and Answers
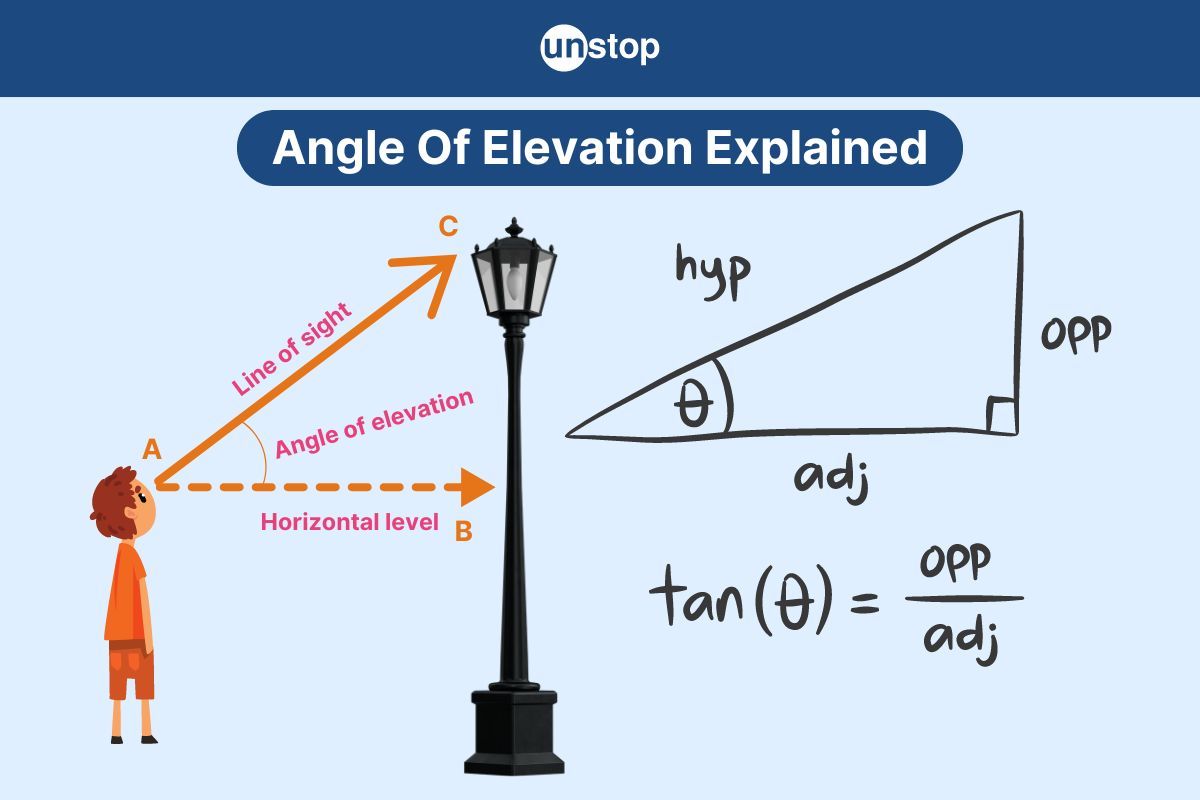
Exploring the concept of the angle of elevation opens a window to understanding how sightlines and distances intertwine. This fundamental trigonometric notion plays a pivotal role in various competitive exams. By grasping the angle of elevation's significance, one can precisely decipher heights, distances, and spatial relationships.
Defining Angle Of Elevation
The angle of elevation in trigonometry describes the angle between the horizontal line (ground) and the line of sight when looking up at an object. When calculating the angle of elevation, you can use trigonometric functions like tangent.
For instance, if you know the height and distance from the object, you can determine the angle using the formula: tan(angle) = height/distance.

Key Terms Used In Angle Of Elevation
Angle: The angle refers to the measurement between two lines intersecting at a point. By recognizing the angle, one can gauge the inclination of an object from the observer's viewpoint.
Horizontal Line: A horizontal line runs parallel to the horizon, aiding in determining height variations. The horizontal line acts as a reference for measuring the object's height above ground level accurately.
Line Of Sight: The line of sight is the straight path along which an observer views an object. The line of sight assists in visualizing how high or low an object is positioned relative to the observer.
Interconnected Nature Of These Terms
These terms are intricately connected when determining the angle of elevation. The angle dictates the steepness of elevation, while the horizontal line provides a baseline for measuring vertical distances.
Simultaneously, the line of sight aligns with the angle to establish a clear perspective on an object's position in relation to its top and base.
Angle of Elevation Formula with Example
Let us now delve into the formula for calculating the angle of elevation:
Tangent
The function of tangent is essential in calculating the angle of elevation.
In a right triangle with angle θ, where θ is one of the acute angles, and with sides labelled as follows:
-
Opposite represents the side opposite to the angle θ.
-
Adjacent represents the side adjacent to the angle θ.
Then, the tangent of angle θ is given by:
tan(θ)= Adjacent/Opposite
If you're standing a certain distance from a tall building and you look up at the top of the building, the angle between your line of sight (looking up) and the horizontal line (your eye level) is the angle of elevation.
Trigonometric Relation
If you know the height of the object (h) and the horizontal distance from the object (d), you can use trigonometry to find the angle of elevation (θ):
tan(θ)=h/d
Solving for θ:
θ=arctan(h/d)
Visual Representation
Imagine a right triangle where:
- The horizontal leg represents the distance from you to the base of the building.
- The vertical leg represents the height of the building.
- The line of sight forms the hypotenuse of the triangle.
The angle of elevation is the angle at the observer's position between the horizontal leg and the line of sight.
Click here to enhance and upskill your quantitative aptitude related to the angle of elevation (trigonometry) right away!
Angle of Elevation vs. Angle of Depression

Let's look at the key differences between the angle of elevation and the angle of depression:
| Angle of Elevation | Angle of Depression |
|---|---|
| Measures the angle above the horizontal line | Measures the angle below the horizontal line |
| Used to calculate heights of objects | Used to calculate depths of objects |
| Typically larger than 0 degrees | Typically smaller than 0 degrees |
| Commonly used in surveying and navigation | Commonly used in construction and engineering |
Angle of Elevation MCQs with Answers
Provided below are some selected questions with answers for you to practice and enhance your quantitative aptitude skill:

Question 1: What is the angle of elevation if you look up at a kite flying at a 45-degree angle above you?
a) 45 degrees
b) 90 degrees
c) 135 degrees
d) None of the above
Solution: a) 45 degree
Explanation: Since the angle is 45 degrees and the tangent of 45 degrees is 1, we have:
tan(45°) = Opposite side / Adjacent side
1 = Opposite side / Adjacent side
Since the opposite side (height of the kite) is equal to the adjacent side (distance between you and the kite) when you are directly below the kite, the angle of elevation is indeed 45 degrees.
Therefore, the angle of elevation when you look up at a kite flying at a 45-degree angle above you is 45 degrees.
Question 2: If the angle of elevation is 30 degrees, how high does a ladder reach if it's 10 meters from a wall?
a) 5 meters
b) 10 meters
c) 15 meters
d) 20 meters
Solution: c) 5 meters
Explanation: Using trigonometry, when the angle of elevation is 30 degrees and the ladder is 10 meters from the wall, we can use the sine function because we have the opposite side (height) and the hypotenuse (length of the ladder). The sine of 30 degrees is 1/2.
So, if the length of the ladder (hypotenuse) is 10 meters, the height it reaches (opposite side) would be (1/2) * 10 meters, which equals 5 meters.
Question 3: What is the height of the tower if the angle of elevation from a point 20 meters away from its base is 60 degrees?
a) 20√3 meters
b) 10√3 meters
c) 20 meters
d) 10 meters
Solution: a) 20√3 meters
Explanation: To find the height of the tower, we can use trigonometry:
As per the given question, we have the angle of elevation = 60 degrees and distance from the tower's base = 20 meters
We can use the tangent function because we have the opposite side (height) and the adjacent side (distance from the tower's base). The tangent of 60 degrees is √3.
So, if the adjacent side (distance from the tower's base) is 20 meters, the height of the tower (opposite side) would be (√3) * 20 meters. Height of the tower = √3 * 20 ≈ 20√3 meters.
Therefore, the height of the tower is approximately 20√3 meters.
Question 4: If the angle of elevation to the top of a building is 45 degrees and you are standing 20 meters away, how tall is the building?
a) 10 meters
b) 20 meters
c) 20√2 meters
d) 40 meters
Solution: c) 20 meters
Explanation: As per the given question, we have the angle of elevation = 45 degrees and distance from the building = 20 meters
We can use the tangent function because we have the opposite side (height) and the adjacent side (distance from the building). The tangent of 45 degrees is 1.
So, if the adjacent side (distance from the building) is 20 meters, the height of the building (opposite side) would also be 20 meters. Therefore, the height of the building is 20 meters.
Question 5: At a certain time of the day, the sun is seen at the angle of 45 degrees. If the shadow of a pole is 10 meters long, what is the height of the pole?
a) 5√2 meters
b) 10√2 meters
c) 5 meters
d) 10 meters
Solution: d) 10 meters
Explanation: As per the question,
the angle of elevation of the sun = 45 degrees
Length of the shadow = 10 meters
tan(45°)= Height/10
The tangent of 45 degrees is 1.
So, solving for the height:
Height=10×tan(45°)=10×1=10
Therefore, the correct answer is 10 meters
Question 6: A ladder is leaning against a wall. The angle of elevation of the ladder is 60 degrees, while the foot of the ladder is 8 meters away from the wall. How long is the ladder?
a) 8 meters
b) 16 meters
c) 8√3 meters
d) 16√3 meters
Solution: b) 16 meters
Explanation: As per the given question,
- Angle of elevation of the ladder = 60°
- Distance of the foot of the ladder from wall = 8 meters
The sine of the angle of elevation is equal to the ratio of the height of the ladder to its length.
sin(60°)=Height/Length of the ladder (sine(60°)= √3/2)
Length of the ladder=Height/sin(60°)
Height=8×sin(60°)= 8×√3/2= 4√3
Now, substituting the height into the formula for the length of the ladder:
Length of the ladder=4√3/√3/2=4√3×2/√3=8×2=16
Hence, the length of the ladder is 16 meters.
Question 7: What is the height of the tower when a tower casts a shadow of 60 meters under the sun at an angle of elevation of 30 degrees?
a) 30 meters
b) 60 meters
c) 90 meters
d) 120 meters
Solution: a) 30 meters
Explanation: As per the given question, we have the length of the tower's shadow= 60 meters and the angle of elevation= 30°
Therefore, height=shadow length×tan(angle of elevation)=60×tan(30°)=60×1/√3= 30 meters.
Question 8: What is the height of the tower if the angle of elevation from a point on the ground to the top of the tower is 60 degrees and the point of observation is 100 meters from the base of the tower?
a) 50√3 meters
b) 173.2 meters
c) 100√3 meters
d) 200 meters
Solution: b) 173.2 meters
Explanation: The tower's height is the tangent of 60 degrees times the distance from the observer (100 meters), which is 100 × tan(60°)= 100×√3 ≈ 173.2 meters.
Question 9: What is the distance of the boat from the base of the cliff if an observer on top of a 100-meter cliff sees the boat at an angle of depression of 45 degrees?
a) 50 meters
b) 100 meters
c) 100√2 meters
d) 200 meters
Solution: b) 100 meters
Explanation: Distance = opposite over tangent (tan 45° = 1), so distance = 100 meters (the opposite side).
Question 10: What is the distance of the building from the point directly below the plane if an aeroplane flying at an altitude of 5 kilometres has an angle of depression of 20 degrees to a building on the ground?
a) 17.3 kilometres
b) 20.4 kilometres
c) 24.4 kilometres
d) 14.5 kilometres
Solution: d) 14.5 kilometres
Explanation: Distance can be calculated as the opposite side of the angle of depression, which is the altitude of the plane divided by the tangent of the angle of depression, i.e., distance = altitude/tan (angle of depression) = 5 / tan(20°) ≈ 14.5 kilometres.
Conclusion
The exploration of the angle of elevation has shed light on its significance in various fields. Understanding the angle of elevation, its concept, essential terms, and calculations can enhance one's ability to accurately calculate height and distance using trigonometric ratios.
Exploring further examples and practising calculations will solidify one's grasp of elevation angles. Embracing these insights will not only sharpen your aptitude skills but also foster a deeper appreciation for trigonometric ratios in everyday tasks.
Time For A Short Quiz
Frequently Asked Questions (FAQs)
1. What is the angle of elevation?
When someone gazes up at something higher than their eyes, they see an angle called the angle of elevation. This angle is made between a flat line and the line of sight going upwards to the object.
2. How is the angle of elevation calculated?
To calculate the angle of elevation, the formula tan(angle) = opposite/adjacent is used. By knowing the height of the object and the distance from the observer, you can determine the angle of elevation.
3. What distinguishes elevation angles from depression angles?
Elevation angles are measured when looking upwards from a horizontal line, while depression angles are measured when looking downwards from a horizontal line. Elevation angles are always positive, whereas depression angles are negative.
4. Can you provide real-world examples where understanding elevation angles is crucial?
Understanding elevation angles is essential in various fields such as engineering, architecture, and surveying. For instance, calculating the angle of elevation is critical in designing ramps for accessibility or determining optimal locations for installing surveillance cameras.
5. Why are horizontal lines important when discussing elevation angles?
Horizontal lines serve as reference points for measuring both elevation and depression angles. They provide a baseline for calculating how high or low an object is relative to the observer's eye level, making it easier to determine accurate angle measurements.
Suggested reads:
Instinctively, I fall for nature, music, humor, reading, writing, listening, traveling, observing, learning, unlearning, friendship, exercise, etc., all these from the cradle to the grave- that's ME! It's my irrefutable belief in the uniqueness of all. I'll vehemently defend your right to be your best while I expect the same from you!
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter
















Comments
Add comment