Mixture and Alligation: Basic Concept, Formulas and Solved MCQs

11 mins read

Understanding how different components combine in a mixture and alligation can be perplexing but essential, especially when it comes to quantitative aptitude tests, be it for placement interviews or competitive exams.

A detailed explanation of the concept and formula with selected questions and answers related to mixture and alligation is provided here in this article. 

Concept of Mixture and Alligation

Mixture refers to a combination of two or more different substances, while alligation is a method used to solve problems related to mixtures.

Mixture and alligation help in determining the quantities of different components needed to create a mixture with specific properties.

The alligation rule states that if two ingredients are mixed to form a mixture, then the ratio of quantities of the two ingredients is inversely proportional to their prices.

Types Of Alligation Questions

Alligation questions typically fall into two categories:

• Simple alligation involves finding the ratio in which two or more ingredients must be mixed to obtain a mixture at a specified price.

• Compound alligation, on the other hand, deals with solutions containing multiple ingredients of different prices.

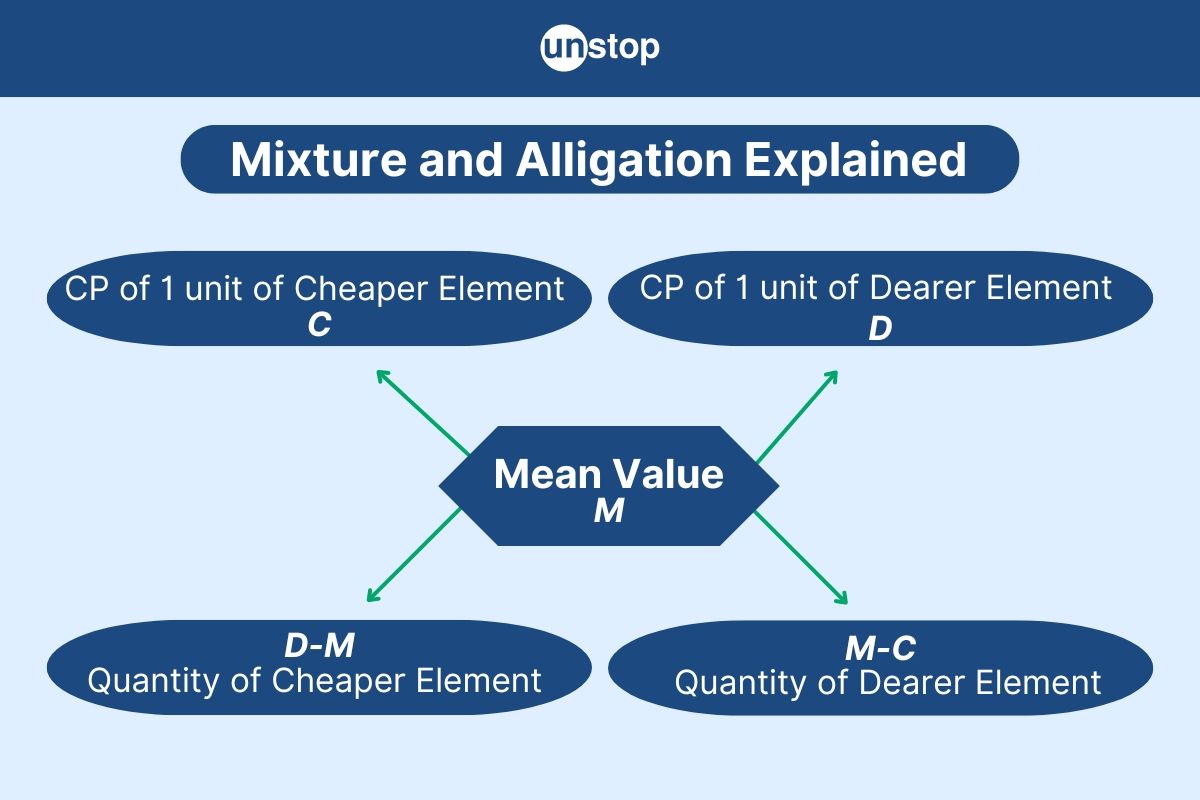
Formula for Solving Mixture & Alligation

To tackle numerical ability problems effectively, it's essential to understand the important formulas related to mixture and alligation. These formulas can significantly simplify the process, making it quicker and more efficient. Provided below are some of the basic formulas related to mixture and alligation:

Formula to find the ratio of Mixture

 Rule of Alligation Formula 

Tips For Solving Mixture And Alligation

Let us study some of the tips to solve mixture and alligation problems:

Practice Consistently

Consistent practice is crucial for mastering mixture and alligation problems. Regularly solving a variety of questions helps in understanding different scenarios and improves problem-solving skills over time.

Utilize Time-Saving Techniques

Implement time-saving techniques to tackle complex mixture and alligation problems efficiently. One such technique is setting up equations systematically, ensuring accuracy while saving valuable time during examinations or assessments.

Conceptual Clarity

Develop a strong conceptual clarity about the principles of mixture and alligation. Understanding the underlying concepts allows for quicker identification of problem types and application of appropriate solution strategies.

Click here to consistently enhance and upskill your quantitative aptitude and reasoning prowess.

Selected Questions With Answers For Practice 

For your practice, we have selected some questions with a detailed explanation of mixture and alligation below:

Question 1. The average salary per head of all workers (Grade A and Grade B) of a company is INR 400. The average salary of 100 Grade-A workers is INR 1000. If the average salary per head of the rest of the Grade-B workers is INR 300, find the total number of workers in the company. 

A) 1000   

B) 800   

C) 500    

D) 700

Solution: D)

Explanation:

Total workers = Number of Grade-A workers + Number of Grade-B workers. Let 'x' be the number of Grade-B workers. So, total workers = 100+x

The average salary of all workers = ₹400. Therefore, the total salary for all workers = ₹400 × (100 + x).

Total salary of Grade-A workers = ₹1,000 × 100 = ₹1,00,000.

The average salary of Grade-B workers = ₹300. So, the total salary for Grade-B workers = ₹300 × x.

Combine total salaries:

₹400×(100+x)=₹1,00,000+₹300×x

Solve for x:

₹40,000+₹400x=₹1,00,000+₹300x

₹400x−₹300x=₹1,00,000−₹40,000

₹100x=₹60,000

x=600

Total number of workers = 100 (Grade-A) + 600 (Grade-B) = 700. 

Question 2. Two types of sugar are priced at ₹40 per kg and ₹60 per kg. In what ratio should they be mixed to obtain a mixture costing ₹50 per kg?

A) 1:1
B) 2:3
C) 1:2
D) 2:1

Solution: A) 1:1

Explanation: 

Difference between ₹60 (costlier sugar) and ₹50 (desired cost) = ₹10

Difference between ₹50 (desired cost) and ₹40 (cheaper sugar) = ₹10

According to the alligation formula, the ratio is the inverse of the differences: ₹10 (from ₹60): ₹10 (from ₹40) = 1:1.

Question 3. A tank contains 500 liters of wine. 50 litres of wine is taken out of it and replaced by water. The process is repeated again. Find the proportion of water and wine in the resulting mixture. 
A) 1 : 4 

B) 41:50 

C) 19:81 

D) 8 :19 

Solution: C) 19:81

Explanation:

The initial amount of wine is 500 litres, of which 50 litres (i.e., 1/10th) is replaced with water. The remaining 9/10th is wine. When the step is repeated, 9/10th of the remaining mixture is wine. So, the amount of wine left = 500 X 9/10 X 9/10 = 405 liters. 

Hence, the amount of water = 95 liters. The ratio of water and wine = 19:81. 

Question 4. A man purchased a table and a chair for INR 2000. He sold the table at a profit of 20% and the chair at a profit of 40%. In this way, his total profit was 25%. Find the cost price (in INR) of the table. 

A) 1500 

B) 900 

C) 1000 

D) 800 

Solution: A) 1500

Explanation:

As per the question, the total cost of the table and chair = ₹2000, the profit on the table = 20%, the profit on the chair = 40% and the overall profit = 25%. 

Let the cost of the table be $T$ and the chair be C.
So, T+C=2000.

Using alligation:

• Difference between chair’s profit (40%) and overall (25%) = 15%.
• Difference between overall (25%) and table’s profit (20%) = 5%.

Thus, the ratio of the cost of the table to the chair is 15:5=3:1.

Since the ratio is $3:1$, the total cost is split into 4 parts (3 parts for the table, 1 part for the chair)

Now, the cost of the table T=3/4×2000=₹1500.

Question 5. A dishonest shopkeeper purchased milk at INR 100 per litre and mixed 10 litres of water in it. By selling the mixture at the rate of INR 100 per litre, he earns a profit of 25%. The quantity of the amount of the mixture that he had was: 

A) 50 litres 

B) 40 litres 

C) 25 litres 

D) 60 litres 

Solution: A) 50 litres 

Explanation:

As per the question, the shopkeeper buys milk at ₹100 per litre and adds 10 litres of water to the milk. He sells the entire mixture at ₹100 per litre and makes a profit of 25%.

Let the quantity of pure milk purchased be x litres.

C.P. of pure milk=100×x=100x

Since the shopkeeper earns a profit of 25%, the Selling Price (S.P.) must be 25% higher than the cost price.

S.P.=C.P.+25%of C.P.=100x+0.25×100x=125x

The shopkeeper added 10 litres of water to the pure milk. So, the total mixture quantity = x litres of milk+10 litres of water.

The selling price per litre = ₹100, and he sells the entire mixture. Thus:

125x=100×(x+10)

125x=100x+1000

125x−100x=1000

x=1000/25=40

Therefore, the total quantity of the mixture is x+10=40+10=50 litres.

Question 6. A milkman stole milk from a can that contained 50% milk, and he replaced what he had stolen with milk having 20% milk. The bottle then contained only 25% milk. How much of the bottle did he steal?

A) 80%

B) 83.33%

C) 85.71%

D) 88.88%

Solution: B) 83.33%

Explanation:

As per the question, initially, the bottle contained 50% milk. The milkman stole some milk and replaced it with another mixture that had 20% milk. After mixing, the final percentage of milk in the bottle became 25%.

Let 'x' be the fraction of the bottle the milkman stole and replaced.
The fraction of milk left after the milkman stole and replaced is (1−x) of the initial 50% milk. The fraction of milk added is x, but it contains only 20% milk.
The final percentage of milk is 25% after the theft and replacement, so the total milk percentage can be written as:
(1−x)×50%+x×20%=25%
(1−x)×50+x×20=25
50−50x+20x=25
50−30x=25
50−25=30x
25=30x
x=25/30=5/6
The milkman stole 5/6 of the bottle, which is approximately 83.33% of the total content.

Question 7. A grocer has two types of wheat. One type costs ₹25 per kg, and the other costs ₹40 per kg. He wants to mix them to get a mixture costing ₹30 per kg. In what ratio should the two types of wheat be mixed?

A) 2:3
B) 3:1
C) 5:3
D) 2:1

Solution: D) 2:1

Explanation:

Difference between ₹40 (costlier wheat) and ₹30 (desired cost) = ₹10

Difference between ₹30 (desired cost) and ₹25 (cheaper wheat) = ₹5

Using alliagation rule, the ratio of the two types of wheat is the inverse of these differences:

Ratio=10:5=2:1.

Question 8. A 10 percent gain is made by selling the mixture of two types of milk at INR 48 per kg. If the type costing INR 61 per kg was mixed with 100 kg of the other, how many kilograms of the former was mixed? 

A) 38 kg

B) 30.5 kg

C) 19 kg

D) Cannot be determined

Solution: D) Cannot be determined

Explanation:

We cannot determine the answer to this question as we do not know the price per kg of the other type of milk. Hence, we cannot find the ratio of mixing that would be required in order to move further in this question.

Question 9. A person purchased a pen and a pencil for INR 15. He sold the pen at a profit of 20% and the pencil at a profit of 30%. If his total profit was 24%, find the cost price of the pen. 

A) INR 10.50 

B) INR 12 

C) INR 9 

D) INR 10 

Solution: C) INR  9

Explanation: As per the question, the total cost of the pen and pencil is INR 15. The profit on the pen is 20%, the profit on the pencil is 30%, and the overall profit is 24%.
Let the cost price of the pen be x, and the cost price of the pencil be 15−x.
Total Profit=24%×15=24/100×15=3.6 
The profit from the pen is 20% of x
Profit from the pen=0.20×x=0.2x
The profit from the pencil is 30% of 15−x
Profit from the pencil=0.30×(15−x)=4.5−0.3x

The sum of the individual profits must equal the total profit:
0.2x+(4.5−0.3x)=3.6
0.2x−0.3x+4.5=3.6
−0.1x+4.5=3.6
Subtract 4.5 from both sides:
−0.1x=3.6−4.5=−0.9
x=−0.9/−0.1=9
The pen cost INR 9.

Question 10. A shopkeeper has two types of rice. One type costs ₹30 per kg, and the other costs ₹50 per kg. He wants to create a mixture that costs ₹40 per kg. In what ratio should he mix the two types of rice?

A) 2:3

B) 2:3

C) 1:1

D) 2:4

Solution: D) 1:1

Explanation: 

Calculate the differences:

Difference between ₹50 (costlier rice) and ₹40 (desired cost) = ₹10

Difference between ₹40 (desired cost) and ₹30 (cheaper rice) = ₹10

Apply the alligation rule:

The ratio of the two types of rice is the inverse of these differences:

Ratio=10:10=1:1

Conclusion

Understanding mixture and alligation, mastering key techniques, and practicing with aptitude quiz challenges are vital steps in enhancing problem-solving skills. The importance of these skills cannot be overstated, as they play a crucial role in various fields requiring quantitative analysis.

Take the opportunity to delve deeper into the realm of mixture and alligation by practicing regularly, seeking additional resources, and expanding your knowledge base. Engage with challenging problems, participate in online classes, and collaborate with peers to sharpen your skills further.

Time For A Short Quiz

Frequently Asked Questions (FAQs)

1. What is mixture and alligation method?

The mixture and alligation method is a mathematical technique used to solve problems related to the mixing of different ingredients at various concentrations to obtain a desired overall mixture. By using the principles of alligation, which involves finding the weighted average of the concentrations of different components, one can easily calculate the quantities needed to achieve a specific mixture.

2. What is an example of a mixture alligation?

An example of a mixture alligation is when different concentrations of two substances are mixed together to create a desired concentration. For instance, if you have a 20% solution of sugar and a 50% solution of sugar, you can use alligation to calculate how much of each solution to mix in order to achieve a final solution with a specific sugar concentration, such as 30%.

3. What is the logic of mixture and alligation?

The logic of mixture and alligation revolves around finding the proportions in which two or more ingredients with different strengths or concentrations should be mixed to obtain a desired strength or concentration in the final mixture.

4. What is the rule of alligation formula?

The rule of alligation formula involves finding the weighted average of two or more components with different concentrations to achieve a desired overall concentration.

5. Can practice with aptitude quiz challenges improve proficiency in mixture and allegation?

Yes, practicing with aptitude quiz challenges that include mixture and alligation questions can enhance proficiency by providing exposure to various problem scenarios. Regular practice helps identify patterns, improve calculation speed, boost confidence levels, and refine problem-solving strategies for better performance in assessments.

Suggested reads:

Boats And Streams: Formula, Top Question With Solution (Aptitude)

Clock Questions: Selected Question & Answer (Aptitude) Explained 

Calendar Questions- Selected Aptitude Questions & Answers

Pipes And Cisterns | Top Selected Question With Answer & Formula

Problems On Age - Mastering Best Aptitude Questions & Solutions