Number Series: Best Selected Reasoning Questions With Answers

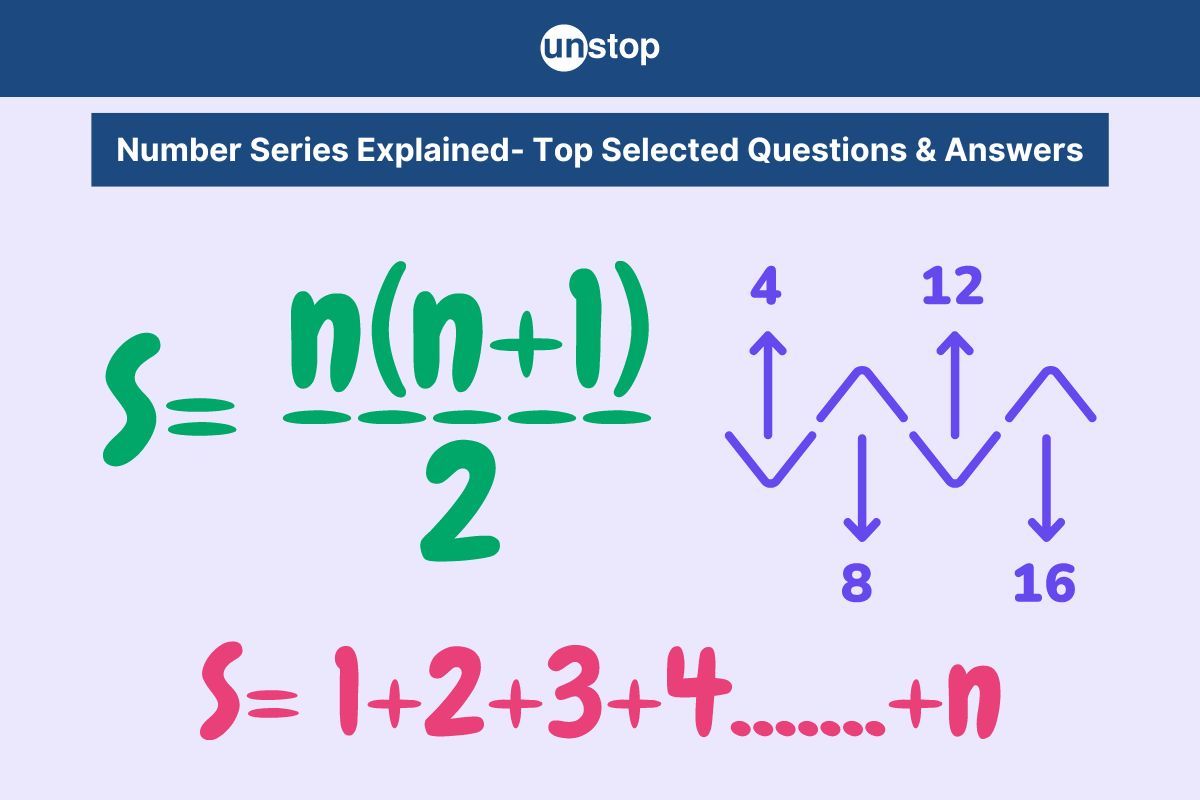
Are you preparing for a placement interview or a competitive exam? Then, understanding number series is essential. This article will explore the pattern, strategy, and selected sample questions related to number series.

It assesses logical thinking, problem-solving ability, time management skills, predictive ability, and numerical proficiency and provides a competitive advantage to candidates.

Understanding Basics Of Number Series

To begin with, let us understand the basics of number series:

Identifying Patterns

Number series are sequences of numbers following a specific order. These patterns involve addition, subtraction, multiplication, or division. Recognizing these patterns is essential for solving number series questions effectively.

Importance Of Pattern Recognition

Identifying the pattern in a number series enables individuals to accurately predict and determine subsequent numbers. By recognizing the underlying pattern, one can efficiently deduce what operation to apply to reach the next number in the sequence.

Types Of Number Series Reasoning Questions

Let us study the types of number series reasoning questions:

Arithmetic Series

Arithmetic number series have a constant difference between consecutive terms.

For example, in the series 2, 4, 6, and 8, the difference is always 2. These types of series are straightforward to identify and solve.

Arithmetic Series:

• Easy to recognize

• Simple to calculate

Geometric Series

Geometric number series involves a constant ratio between consecutive terms.

For instance, sequences 3, 6, 12, and 24 multiply each term by a consistent factor (in this case, by 2).

Geometric Series:

• Consistent multiplication factor

• Requires understanding ratios

Fibonacci Sequence

In the Fibonacci sequence, every number is the result of adding together the two numbers that came before it. The sequence starts with numbers zero and one.

A suitable example of the Fibonacci series is:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

Each number (after the first two, 0 and 1) is the sum of the two preceding numbers. 

For instance, 1 is the sum of 0 and 1, 2 is the sum of 1 and 1, 3 is the sum of 1 and 2, and so on.

Fibonacci Series:

• Begins with zero and one

• Each number results from adding its two predecessors

Addition & Multiplication In Number Series

Let us study the addition and multiplication in number series:

Addition-Based Number Series

Number series that are addition-based involve determining each term by adding a particular value to the term that precedes it.

For example, if a series starts with 3 and adds 5 successively, the sequence would be 3, 8, 13, 18... The difference between consecutive terms remains constant.

Multiplication-Based Number Series

Multiplication-based number series involves multiplying the previous term by a specific value to obtain the next term.

If a sequence begins with 2 and multiplies by 3 consecutively, it will go like this: 2, 6 (2x3),18 (6x3),54...

Square & Cube-Based Number Series Patterns

Let us study the square and cube-based number series patterns:

Square Patterns

A square-based number series involves squaring the terms or using square numbers in the pattern. This means each term is obtained by multiplying a particular number by itself.

When odd numbers are squared in a series, the sequence follows this pattern: 1 squared equals 1, 3 squared equals 9, and 5 squared equals 25.

Cube Patterns

Cube patterns in number series involve the cubes of consecutive numbers or a pattern based on cubic relationships between the numbers. When looking at a number series, you might encounter a pattern like cubing multiples of three.

For instance, if you cube 3, you get 27. And if you cube 6, the result is 216.

Missing Terms & Arranging Sequences

Let us understand how to identify missing terms and arrange sequences in number series:

Finding Missing Numbers

Missing term questions are common. These questions require identifying the value of a term that completes a given sequence.

For example, finding the missing number would complete the pattern in the series 2, 4, 6, _, 10.

Arranging Sequence Logic

Arranging sequences involves rearranging given terms to form a logical pattern. Following specific logic, arranging numbers can be based on their ascending or descending order.

Here's an example of arranging sequence logic in a number series:

6, 9, 12, 15, 18, ...

In this sequence, each number increases by 3. The logic is to add 3 to the previous number to get the next number. So, the sequence can be described as adding 3 to each preceding number to generate the next number.

Tricks & Tips For Solving Number Series

Let us study the tricks and strategies for solving number series questions:

Identify Patterns Quickly

To solve number series questions efficiently, look for common differences or ratios between consecutive terms. By identifying these patterns promptly, you can decipher the sequence faster.

For example, in a sequence like 2, 4, 6, 8... the common difference is +2.

Simplify Complex Sequence

Break down complex patterns when faced with intricate patterns in number series problems, break them down into simpler components. 

For example, a complex pattern in a number series:

3, 8, 18, 38, 78, ...

This sequence increases by progressively larger increments. Upon closer examination, we can see that each term is generated by doubling the previous term and then adding the next odd number:

3×2+2 = 8

8×2+2 = 18

18×2+2 = 38

38×2+2 = 78

Trial & Error Approach

If traditional strategies fail to unveil the pattern in a number series, resort to trial and error or backward calculation methods. Sometimes, trying different values or working backwards from the end of a sequence can swiftly lead you to the correct answer.

For example, let us look at this number series:

2, 5, 10, 17, 26, ...

At first glance, there doesn't seem to be an obvious pattern. So, we can use trial and error by trying different operations or relationships between the numbers to see if we can find a pattern.

Let's try adding consecutive odd numbers to each term:

2+3=5

5+5=10

10+7=17

17+9=26

To find the next number in the series, add 26 and 11 together to get 37. This pattern involves adding consecutive odd numbers, starting from 3.

Regular Practice

Consistent practice is key to mastering number series. The more you practice, the better you will become at identifying sequences and predicting the next numbers.

As a fresher looking to sit for an interview placement or a student looking forward to taking competitive exams, click here to access some of the most reliable onlines resouces.

It will enhance and upskill your knowledge on varied topics ranging from number series, analogy, statement and conclusion, data sufficiency, and more.

Selected Sample Questions With Detailed Solutions

Here, we present you the top selected sample questions of a number series that will have relevance in placement interviews and competitive examinations:

Question 1. Find the 20th term of the arithmetic series: 3, 7, 11, 15,...

Solution: In the given sequence: 3, 7, 11, 15,...

The common difference between consecutive terms is 7-3=4.

To find the 20th term, we can start with the first term (3) and add the common difference (4) nineteen times:

3+4+4+4+ ... (19 times)

This can also be expressed as 3+4×19

Now, calculate: 3+4×19=3+76=79

So, the 20th term of the sequence is 79.

Question 2. Find the 30th term of the arithmetic series: 10, 15, 225,…

Solution: In the given series, we notice that each term increases by 5.

To find the 30th term, we can start with the first term (10) and add the common difference (5) twenty-nine times to reach the 30th term: 10+5+5+5+….+5.

Since the common difference is added twenty-nine times, we have 29×5=145.

Adding this to the first term: 10+145=155. So, the 30th term of the series is 155.

Question 3. What is the sum of the first 5 terms of the geometric series where the first term is 3, and the common ratio is 2?

Solution: Given that the first term is 3 and the common ratio is 2, the series looks like this: 3, 6, 12, 24, 48,…

To find the sum of the first 5 terms, we can add them up: 3+6+12+24+48=93. So, the sum of the first 5 terms of this geometric series is indeed 93.

Question 4. Consider the series: 4, 7, 10, 13, 16,... What is the next number in the series, and what is the rule governing the pattern?

Solution: In the given series: 4, 7, 10, 13, 16,....we can observe that each number is increasing by 3. So, the rule governing the pattern is adding 3 to the previous number to get the next number.

To find the next number in the series, we just need to add 3 to the last number in the series: 16+3 = 19.. So, the next number in the series is 19.

Question 5. Consider a sequence where each term is the sum of the two preceding terms. If the sequence starts with 1 and 2, what is the 10th term in this sequence?

Solution: We can find the 10th term using the Fibonacci method of finding a number series sequence. The sequence starts with 1 and 2: 1, 2, 3, 5, 8, 13, 21, 34, 55,.....

To find the next term, we add the two previous terms: 2+1=3, 3+ 2=5, 5+3=8 etc.

Continuing this pattern, we can find the 10th term:

1st term: 1

2nd term: 2

3rd term: 1+2=3

4th term: 2+3=5

5th term: 3+5=8

6th term: 5+8=13

7th term: 8+13=21

8th term: 13+21=34

9th term: 21+34=55

10th term: 34+55=89

So, the 10th term in the Fibonacci sequence is 89.

Questions 6. Consider the series 2, 5, 9, 14, 20, etc. (Each number in the series is obtained by first multiplying the previous number by a certain factor and then adding a constant value.) What is the next number in the series, and what are the specific multiplication and addition rules governing the pattern?

Solution: To find the next number in the series and determine the specific multiplication and addition rules governing the pattern, let's examine the differences between consecutive terms:

2→5: The difference is 5-2=3

5→9: The difference is 9-5=4

9→14: The difference is 14-9=5

14→20: The difference is 20-14=6

We can observe that the differences between consecutive terms are increasing by 1 each time. This suggests that the series is increasing at an accelerating rate.

Now, let's look at the multiplication factors between consecutive terms:

2×1=2

5×2=10

9×2=18

14×2=28

20×2=40

We can see that each term is multiplied by 2.

So, the next number in the series is obtained by adding the next difference (7) to the last term (20) and then multiplying the result by the common factor (2):

20+7=27

27×2=54

Therefore, the next number in the series is 54.

The multiplication rule multiplies each term by 2, and the addition rule adds increasing consecutive integers to the previous term.

Question 7. Consider the series: 3, 12, 27, 48,.....What is the next number in the series, and what is the rule governing the pattern?

Solution: In the given series: 3, 12, 27, 48,...

To find the pattern, let's analyze the differences between consecutive terms:

• From 3 to 12: 12−3=9

• From 12 to 27: 27−12=15

• From 27 to 48: 48−27=21

The differences between consecutive terms are increasing by 6 each time.

Now, let's examine the differences of consecutive differences: 15-9=6

This suggests that the rule governing the pattern might involve adding consecutive odd numbers to the previous term.

Let's verify this by finding the next number using this pattern: Adding 27 and 21, we get 48 + 27 + 21 = 96.

So, the next number in the series is 96. The rule governing the pattern is adding consecutive odd numbers to the previous term, starting from 9.

Question 8. Consider the series: 3, 8, 15, ? 31, 42, 55,... What is the missing number in the series, and what is the rule governing the pattern?

Solution: To find the missing number and the pattern governing the series, let's analyze the differences between consecutive terms:

• 8−3=5

• 15−8=7

• 31−15=16

• 42−31=11

• 55−42=13

By observing the differences, we can notice that they are alternating between consecutive odd numbers and consecutive even numbers.

Now, let's apply this pattern to find the missing number: The difference between 16 and 7 is 16−7=9. This suggests that the next odd number difference would be 16+9=25.

So, to find the missing number, we add 25 to the last number in the series: 31+25=56. 

Therefore, the number missing in the series is 56, and the pattern governing the series alternates between consecutive odd and even numbers.

Question 9. Consider the series 3, 7, 13, 21, 31, ?.

Solution: To find the pattern, calculate the differences between consecutive terms:

• 7-3=4
• 13-7=6
• 21-13=8
• 31-21=10

The differences are 4, 6, 8, and 10, which increase by 2 each time. Following the pattern, the next difference should be 12 (10 + 2). Add the next difference to the last term in the series: 31 + 12 = 43. Therefore, the next number in the series is 43.

Question 10. Consider the series 2, 6, 12, 20, 30, ?

Solution: Calculate the differences between consecutive terms:

• 6-2=4
• 12-6=6
• 20-12=8
• 30-20=10

The differences are 4, 6, 8, and 10, which increase by 2 each time. Following the pattern, the next difference should be 12 (10 + 2). Add the next difference to the last term in the series: 30+12 = 42

Therefore, the next number in the series is 42.

Apart from learning about logical reasoning questions, you can also find resources ranging from computer fundamentals, coding, interview preparation, etc., by clicking here.

Conclusion

The exploration of number series logic has shed light on the diverse patterns and strategies essential for mastering this reasoning skill. Understanding the basics, recognizing different types of sequences, and employing tricks for efficient problem-solving are key takeaways from this comprehensive guide. 

Practice is paramount to excel in number series. By utilizing the provided sample questions and implementing the suggested tips, individuals can confidently sharpen their skills and approach these problems. 

Frequently Asked Questions (FAQs)

1. What are number series logic questions?

Number Series Logic questions involve identifying patterns in a sequence of numbers and predicting the following number based on that pattern. These questions test analytical and logical reasoning skills.

2. How can one excel in solving number series questions?

To excel in solving Number Series questions, practice regularly to familiarize yourself with various patterns, use systematic approaches for each type of series, and understand basic mathematical operations like addition, multiplication, squares, and cubes.

3. Why is it essential to identify missing terms in a number series?

Identifying missing terms helps establish the underlying pattern or rule governing the series. By recognizing these patterns accurately, you can predict future terms effectively and solve complex number series problems efficiently.

4. What strategies can be employed for solving square-based and cube-based number series patterns?

For Square-based and Cube-based Number Series Patterns, focus on recognizing squared or cubed values within the sequence. Look for consistent differences between consecutive numbers or examine how square/cube values relate to each other within the series.

5. How do tricks aid in solving number series questions?

Tricks such as breaking down sequences into smaller parts and looking for common arithmetic operations or geometric progressions help simplify complex number series problems. Utilizing tricks enhances efficiency when tackling challenging patterns within a sequence.

Suggested reads:

• CAT 2024: Tips To Score Well In Logical Reasoning And Data Interpretation (LRDI) Section
• What Is Bitsat Exam?: Find Application Process, Exam Pattern & More
• 50+ Power BI Interview Questions (With Answers) For 2024 Job Interviews
• 70+ Agile Interview Questions And Answers For 2024 Job Interviews
• How To Become An Astronaut In India | Qualification & Requirement