Profit And Loss: Basic Concepts, Formulas, Questions & Answers 

12 mins read

Understanding the concept of profit and loss is essential whether you're preparing for a competitive exam or simply looking to improve your quantitative aptitude skills. Mastering the basic concepts and formulas and practising with questions can help you excel in this area of the exam.

Don't let the complexity of the problems overwhelm you; instead, use them as opportunities to enhance your problem-solving abilities and excel in the exam.

Basic Concepts Of Profit And Loss

Profit and loss are fundamental concepts in business and finance, representing the difference between the amount earned from selling goods (revenue) and the amount spent to produce or acquire them.

Profit And Loss Relationship

If the cost price is less than the selling price, then a profit is made. Conversely, if the cost price is higher than the selling price, a loss occurs. Understanding this relationship is crucial for effective financial management.

Cost Price & Selling Price

The cost price refers to the amount a business pays to purchase or produce an item, while the selling price is the value at which it is sold. The interest between these two values determines whether a profit or loss is incurred.

Marked Price

Marked price, also known as market price, is the initial value assigned to a product before any discounts are applied. It serves as a reference point for both sellers and buyers, indicating the value of the item without considering any reductions.

Determining Selling Price

The selling price is derived from the cost price of an item with additional considerations such as operating expenses and desired profit margin. By adding these factors to the cost price, businesses arrive at a selling price that ensures they cover all costs and generate income.

For example, if a product's cost price is ₹50 and the business aims for a 20% profit margin, the selling price would be calculated by adding the margin to the cost: ₹50 + (₹50 x 0.20) = ₹60. This ensures that after covering costs, including production and operational expenses, the business makes a profit on each sale.

Calculating Discounts

To determine the discount percentage, one must understand how it relates to both marked and selling prices. The formula for calculating discount percentages based on these prices is straightforward:

Discount % = ((Marked Price - Selling Price) / Marked Price) x 100

For instance, if an item's marked price is ₹100 and it is sold for ₹80, the discount percentage would be (₹100 - ₹80) / ₹100) x 100 = 20%. This calculation shows how much of a reduction in price was offered to customers.

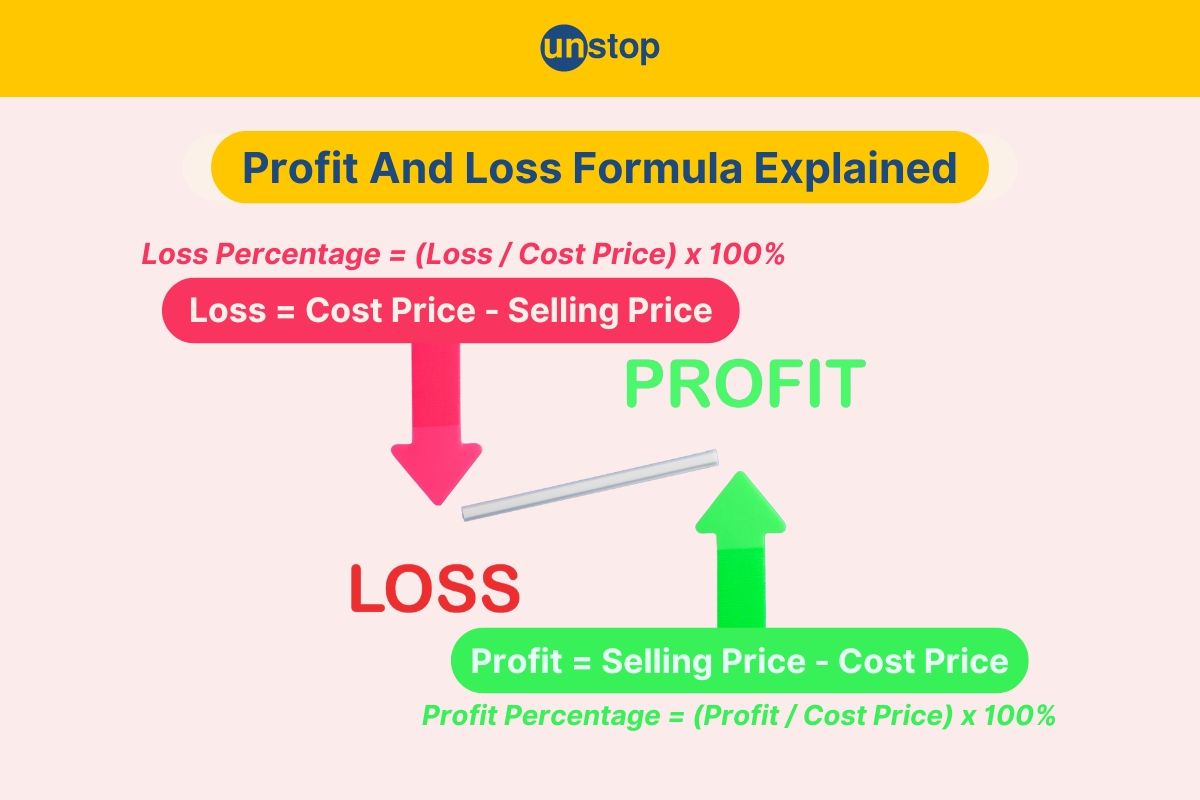
Formulas For Calculating Profit And Loss

Let us study the formulas for calculating profit and loss:

Profit Formula

To calculate overall profit, subtract the cost price from the selling price. The formula is:

Profit = Selling Price - Cost Price

Loss Formula

To determine a loss, subtract the selling price from the cost price:

The formula is: 

Loss = Cost Price - Selling Price

Net Profit Calculation

The net profit can be found by deducting all expenses from the total revenue generated. The formula is:

Net Profit = Total Revenue - Total Expenses

Profit Percentage Calculation

Calculating profit percentage involves dividing the profit by the cost price and then multiplying by 100%:

Profit Percentage = (Profit / Cost Price) x 100%

For example, let us say that an item is bought for ₹50 and sold for ₹70. Using the profit formula: ₹70 - ₹50 = ₹20 (profit).

Calculating profit percentage: (₹20 / ₹50) x 100% = 40%

Loss Percentage Calculation

Similarly, to find the loss percentage, divide the loss by the cost price and multiply by 100%:

Loss Percentage = (Loss / Cost Price) x 100%

For example, let us say that a product costing ₹80 is sold for $60. Applying the loss formula: ₹80 - ₹60 = ₹20 (loss). Determining loss percentage: (₹20 / ₹80) x 100% = 25%

Click here to enhance further and upskill your quantitative aptitude related to profit and loss right away!

Examples Of Profit And Loss

Let us consider some examples of profit and loss:

Profit Scenarios

Imagine a small bakery that sells fresh bread daily. Each loaf costs ₹5 to make, including ingredients and labour. If the bakery sells 100 loaves in a day, its total revenue would be ₹500 (100 loaves x ₹5 each). However, if the daily expenditures amount to ₹300, the bakery's profit for that day would be ₹200 (₹500 - ₹300).

Let's consider another example in the tech industry. A software company develops an app that generates revenue through in-app purchases. If the company earns ₹10,000 in revenue monthly but incurs expenses of ₹7,000 (including development costs and salaries), its monthly profit would be ₹3,000.

Loss Scenarios

Picture a clothing store that faces declining sales due to changing fashion trends. If the store's monthly revenue drops to ₹3,000 while its fixed costs remain at ₹5,000, it will incur a monthly loss of ₹2,000.

In another scenario, a restaurant invests in renovating its space to attract more customers but fails to see an increase in revenue. If the renovation costs amount to ₹15,000 and the monthly revenue remains stagnant at ₹8,000 while operating expenses total ₹10,000, the restaurant will experience a significant loss of ₹7,000 for that month.

Profit & Loss Questions With Detailed Solution 

Provided below are some selected questions with detailed answers for you to practice and enhance your quantitative aptitude skills:

Question 1. A company sells a product at ₹50 per unit. The fixed costs are ₹10,000, and variable costs per unit are ₹20. If the company sells 500 units, what will be its profit?

A) ₹5,000

B) ₹10,000

C) ₹15,000

D) ₹20,000

Solution: A) ₹5,000

Explanation: Total Revenue = Selling price per unit×Number of units sold = ₹50×500 = ₹25,000

Total Costs = Fixed Costs + Variable Costs = ₹10,000 + (₹20×500) = ₹20,000

Profit = Total Revenue - Total Costs = ₹25,000 - ₹20,000 = ₹5,000

Therefore, the company's profit from selling 500 units is ₹5,000.

Question 2. A bookstore sells each textbook for₹30. The fixed costs of operating the bookstore are ₹1,000, and the variable costs per textbook are ₹10. If the bookstore sells 200 textbooks, what will be its profit?

A) ₹2,000

B) ₹3,000

C) ₹4,000

D) ₹5,000

Solution: B) ₹3,000

Explanation: Total Revenue: ₹30 per textbook×200 textbooks = ₹6,000

Total Costs: ₹1,000 (Fixed) + (₹10 per textbook×200 textbooks) = ₹3,000

Profit: Total Revenue - Total Costs = ₹6,000 - ₹3,000 = ₹3,000

Hence, the company's profit from selling 200 textbooks is ₹3,000.

Question 3. A bakery sells cakes for ₹20 each. The fixed costs of running the bakery are ₹500, and the variable costs per cake are ₹15. If the bakery sells 30 cakes, but due to a production error, 10 cakes are damaged and unsellable, what will be its loss?

A) ₹50

B) ₹150

C) ₹200

D) ₹250

Solution: C) ₹200

Explanation: Total Revenue: ₹20×30 = ₹600

Total Costs: Fixed costs (₹500) + Variable costs (₹15×30) = ₹950

Loss: Only 20 cakes are sold due to damage, yielding a revenue of ₹400.

Loss = Total Costs (₹950) - Revenue from sold cakes (₹400) = ₹550

However, the loss incurred only accounts for the damage, which is ₹200.

Therefore, the bakery incurs a loss of ₹200.

Question 4: A toy store sells each toy for ₹10. The fixed costs of operating the store are ₹200, and the variable costs per toy are ₹5. If the store sells 50 toys, what will be its profit?

A) ₹100

B) ₹50

C)₹200

D) ₹250

Solution: B) ₹50

Total Revenue: ₹10 per toy×50 toys =₹500

Total Costs: Fixed costs (₹200) + Variable costs (₹5 per toy×50 toys) = ₹450

Profit: Total Revenue (₹500) - Total Costs (₹450) = ₹50

Therefore, the store's profit from selling 50 toys is ₹50.

Question 5. A company sells widgets for ₹20 each. The cost price of each widget is ₹15. If the company sold 100 widgets, what is its profit?

A) ₹500

B) ₹750

C) ₹1,000

D) ₹1,250

Solution: A) ₹500

Explanation: Profit per Widget: Selling Price - Cost Price = 20 - 15 = ₹5

Total Profit: Profit per Widget×Number of Widgets Sold = 5×100 = ₹500

Therefore, the company's profit from selling 100 widgets is ₹500.

Question 6: A textile shop sells sarees for ₹2000 each. The shop incurs a cost price of ₹1500 for each saree. If the shop sells 50 sarees, but due to a quality issue, 10 sarees are returned by customers, each fetching a refund of ₹1500, what is the net profit of the shop?

A) ₹25,000

B) ₹30,000

C) ₹35,000

D) ₹40,000

Solution: C) ₹35,000

Explanation: Total Revenue: Selling price per saree×Number of sarees sold = ₹2000×50 = ₹1,00,000

Total Costs: Cost price per saree * Number of sarees sold = ₹1500×50 = ₹75,000

Refunds: Number of returned sarees * Refund per saree = 10×₹1500 = ₹15,000

Net Profit: Total Revenue - Total Costs - Refunds = ₹1,00,000 - ₹75,000 - ₹15,000 = ₹10,000

Therefore, the net profit of the shop is ₹10,000. However, since the question asks for the net profit after refunds, we need to subtract the refund amount from the calculated profit:

Net Profit = ₹10,000 - ₹15,000 = -₹5,000

However, this implies a loss. Thus, the correct answer should be:

Net Loss = ₹5,000

Since this option is not provided, the closest answer would be the one without considering the refunds:

(Note: It's important to recognize that the refunds significantly impact the profit/loss scenario.)

Question 7: A jewellery store sells gold bangles for ₹30,000 each. The cost price of each gold bangle is ₹25,000. With a sudden rise in demand, the store decides to offer a discount of 10% on the selling price. If the store manages to sell 20 gold bangles, what is its net profit?

A) ₹1,00,000

B) ₹1,50,000

C) ₹40,000

D) ₹2,50,000

Solution: C) ₹40,000

Explanation: Selling Price after Discount: ₹30,000 - 10% = ₹30,000 - ₹3,000 = ₹27,000 per bangle

Total Revenue: Selling price per bangle * Number of bangles sold = ₹27,000×20 = ₹5,40,000

Total Costs: Cost price per bangle * Number of bangles sold = ₹25,000×20 = ₹5,00,000

Net Profit: Total Revenue - Total Costs = ₹5,40,000 - ₹5,00,000 = ₹40,000

Therefore, the net profit of the jewellery store is ₹40,000.

Question 8: A grocery store sells basmati rice for ₹120 per kilogram with a 15% profit margin, while it sells pulses for ₹80 per kilogram with a 20% profit margin. If the store sells 50 kilograms of basmati rice and 80 kilograms of pulses and incurs fixed costs of ₹5000, what is the overall profit or loss of the store?

A) ₹600

B) ₹800

C) ₹2820

D) ₹1200

Solution: C) ₹2,820

Explanation: Basmati rice profit per kilogram = 15% of ₹120 = ₹18

Total profit from selling 50 kilograms of basmati rice = ₹18×50 = ₹900

Pulses profit per kilogram = 20% of ₹80 = ₹16

Total profit from selling 80 kilograms of pulses = ₹16×80 = ₹1,280

Total Profit: Adding profits from basmati rice and pulses = ₹900 + ₹1,280 = ₹2,180

Subtracting the fixed costs of ₹5,000 from the total profit = ₹2,180 - ₹5,000 = -₹2,820. Therefore, the store incurs an overall loss of ₹2,820.

Question 9: A bookstore sells each novel for ₹200. The cost price of each novel is ₹150. If the store sells 50 novels, what is its overall profit?

A) ₹2,000

B) ₹2,500

C) ₹3,000

D) ₹3,500

Solution: B) ₹2,500

Explanation: Profit per Novel: Selling price - Cost price = ₹200 - ₹150 = ₹50

Total Profit: Profit per novel×Number of novels sold = ₹50×50 = ₹2,500

Therefore, the overall profit of the store is ₹2,500.

Question 10: In a class of 50 students, 70% passed the math exam, and 80% passed the science exam. If 60% of the students passed both exams, how many students passed exactly one exam?

A) 8

B) 10

C) 12

D) 15

Solution: D) 15

Explanation: Students who Passed Math: 70% of 50 = 0.70×50 = 35

Students who Passed Science: 80% of 50 = 0.80×50 = 40

Students who Passed Both Exams: 60% of 50 = 0.60×50 = 30

Students who Passed Exactly One Exam: Total students who passed math + Total students who passed science - Students who passed both exams = 35 + 40 - 30 = 45 - 30 = 15.

Therefore, the number of students who passed exactly one exam is 15.

Conclusion

You've now grasped the fundamentals of profit and loss and mastered the calculations like a pro. By delving into examples and solving problems, you've honed your skills to maximize profits effortlessly.

Engage with practice questions to solidify your understanding and boost your confidence in tackling quantitative aptitude related to profit and loss. Keep practicing, stay curious, and watch your proficiency in profit and loss calculations soar!

Time For A Short Quiz

Frequently Asked Questions (FAQs)

1. What are the basic concepts of profit and loss?

The basic concepts of profit and loss involve revenue exceeding expenses for profit and expenses exceeding revenue for loss. It is a fundamental aspect of understanding the financial performance of a business.

2. How can I calculate profit and loss using formulas?

Formulas for calculating profit and loss key formulas include:

• Profit = Selling Price - Cost Price

• Loss = Cost Price - Selling Price

3. Can you provide examples to clarify profit and loss calculations?

Here is an example of profit and loss: If an item costs ₹50 and is sold for ₹70, the profit is $20. Conversely, if it sells for ₹40, the loss incurred is ₹10.

4. How can I practice profit and loss problems effectively?

Regularly practising solved problems and attempting new ones sharpens your skills in profit and loss calculations. This hands-on approach boosts confidence and proficiency in applying mathematical concepts to real-world scenarios.

5. Where is profit and loss mostly used?

Profit and loss problems are mostly used in business settings to analyze financial performance and make strategic decisions. They are also commonly used in educational settings to teach students about financial concepts and calculations.

Suggested reads: 

• What Is Mensuration: Formulas With Top Selected Question & Answer
• Harmonic Progression- Formula With Selected Questions & Answers 
• Mixture And Alligation: Explained With Selected Question & Answer
• Boats And Streams: Formula, Top Question With Solution (Aptitude)
• Clock Questions: Selected Question & Answer (Aptitude) Explained