- Step 1: The Groundwork
- Step 2: The Three Sections
- Step 3: Practice Makes Improvement
- The Secret Ingredient
- Understanding Basics Of Number Series
- Types Of Number Series Reasoning Questions
- Addition & Multiplication In Number Series
- Square & Cube-Based Number Series Patterns
- Missing Terms & Arranging Sequences
- Tricks & Tips For Solving Number Series
- Selected Number Series Questions With Solutions
- Frequently Asked Questions (FAQs)
- Must Know Terminologies in Blood Relation Questions
- Basic Approaches to Solve Blood Relation Questions
- Types Of Blood Relation Questions
- Tips For Solving Blood Relation Questions
- Multiple Choice Questions (MCQs) with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Letter Series In Logical Reasoning
- Types Of Letter Series Patterns
- Tips For Solving Letter Series Reasoning
- Best Practice Question Samples With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basics of Problems On Age-Related Questions
- Formula to Solve Problems on Ages-Related Questions
- Types of Age-Related Questions & Examples
- Tips & Tricks for Solving Ages Problems
- Best MCQs on Problems on ages with solved answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition of Calendar
- Understanding Days of the Week
- What is a Leap Year?
- Concept of Odd Days in a Century
- Tips For Solving Calendar Reasoning Questions
- Best Calendar Reasoning Questions with Answers (MCQs)
- Frequently Asked Questions (FAQs)
- Basic Concepts of Clock
- Structure of a Clock
- Angle Equilavalence in Clock
- Tips For Solving Clock Questions
- Selected Clock Questions & Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding The Concept Of Direction Sense
- Tips For Effective Problem-Solving In Direction Sense
- Practical Test Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Dice Reasoning
- Dice Numbers In Dice Reasoning
- Classification Of Dice
- Constructed Vs Deconstructed Dice
- Tricks & Tips For Solving Dice Problems
- Practice MCQs With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Alphanumeric Series Defined
- Alphanumeric Series In Reasoning Tests
- Tips & Strategies For Solving Alphanumeric Series
- Practice Sample Questions With Detailed Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept Of Mirror Image Reasoning Explained
- Important Terms In Mirror Image Reasoning
- Types Of Mirror Images
- Identifying Correct Mirror Image
- Finding Clock's Mirror Image
- Tips To Solve Mirror Images
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept & Overview Of Input-Output
- Input-Output In Competitive Exams
- Types Of Input-Output Problems
- Strategies, Tips & Tricks For Solving Reasoning Questions
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Finding The Odd One Out
- Tricks And Tips
- How to Find The Odd One Out?
- Solved MCQs with Detailed Explanation
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Key Concepts
- Exploring Different Ranking Types
- Formula And Application Of Order And Ranking
- Tips For Solving Order & Ranking
- Selected Practice Questions And Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Importance Of Pipes & Cistern Aptitude
- Key Terminologies used in Pipes and Cisterns
- Pipes and Cisterns Formula with Examples
- Pipes and Cisterns Shortcut Tricks
- Tips For Solving Pipes & Cistern Problems
- Selected Questions & Answers For Practice (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Key Concept in Boats and Streams
- Formulas Of Boats & Streams
- Distance & Time Formula
- Tips For Solving Boats & Streams Questions
- Selected Practice Questions With Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Concept of Mixture and Alligation
- Types Of Alligation Questions
- Formula for Solving Mixture & Alligation
- Tips For Solving Mixture And Alligation
- Selected Questions With Answers For Practice
- Conclusion
- Frequently Asked Questions (FAQs)
- Concepts and Definitions Related to Time and Work
- Important Time And Work Formulas
- Tricks and Tips to Solve Time & Work Questions
- Time And Work MCQs with Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Harmonic Progression(HP)?
- Formula to find the nth Term in Harmonic Progression
- Formula to find the Sum of the nth Term in HP
- What is Harmonic Mean?
- Harmonic Progression Solved Best MCQs
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Mensuration in Maths?
- What are 2D figures in Mensuration?
- What are 3D figures in Mensuartion?
- Basic Terminologies In Mensuration
- Basic 2D Formulas in Mensuration
- Basic 3D Formulas in Mensuration
- 2D vs 3D in Mensuration
- Solved Questions With Solutions (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Relationship Between Time, Speed And Distance
- Conversion Units Time, Speed And Distance
- Average & Relative Speed: Two Trains Moving in the same or opposite direction
- Solved MCQs on Time, Speed And Distance
- Conclusion
- Frequently Asked Questions (FAQs)
- What is Simplification in Maths?
- BODMAS Rule in Simplification Explained
- Simplification & Approximation Relation
- Key Terms in Simplification
- Examples Of Simplification Techniques
- Simplification Questions With Solved Answers (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Height And Distance Important Terms
- Right Angled Triangle In Trigonometry
- Trigonometric Ratios
- Solved Examples For Better Understanding
- Height And Distance Applications In Trigonometry
- Height And Distance Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Interest Types
- Simple Interest Vs. Compound Interest
- Selected Solved Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Basic Concepts Of Profit And Loss
- Determining Selling Price
- Calculating Discounts
- Formulas For Calculating Profit And Loss
- Examples Of Profit And Loss
- Profit & Loss Questions With Detailed Solution
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Angle Of Elevation
- Key Terms Used In Angle Of Elevation
- Angle of Elevation Formula with Example
- Angle of Elevation vs. Angle of Depression
- Angle of Elevation MCQs with Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining HCF And LCM
- Calculation Methods Of HCF And LCM
- HCF By Prime Factorization Method
- LCM By Prime Factorization Method
- Difference Between HCF And LCM
- HCF & LCM Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- What is fraction and decimal?
- Understanding Decimal Fraction
- Place Value in Decimal Fraction
- Mathematical Operations with Decimal Fraction
- Practice with Solved Examples
- Summary
- Frequently Asked Questions
- All About Decimals
- All About Fractions
- How to Convert a Decimal into Fraction
- Simple vs Recurring Decimals
- Converting Recurring Decimals to Fractions
- Conversion Charts
- Practice Questions (With Solutions)
- Closing Thoughts
- Frequently Asked Questions
- What is Arithmetic Mean?
- Arithmetic Mean Formula- Ungroup Data & Group Data
- Merits of Arithmetic Mean
- Demerits of Arithmetic Mean
- Alternatives to Arithmetic Mean
- What is the Weighted Arithmetic Mean?
- Arithmetic vs. Geometric Mean
- Arithmetic Mean Application in Statistical Analysis
- Arithmetic Mean Practice Questions with Explanation
- Frequently Asked Questions
- What is Geometric Progression?
- Key Properties of Geometric Progression
- General Form Of Geometric Progression
- General Term or the Nth Term of Geometric Progression
- The sum of nth Terms of GP
- Types Of Geometric Progression
- Solved Questions and Answers of GP
- Conclusion
- Frequently Asked Questions (FAQs)
- Average in Maths
- Average Formula in Maths
- Differentiating Types of Average
- How to Calculate Average of Negative Numbers?
- Practical Applications of Averages
- Average Questions For Practice
- Frequently Asked Questions
- What is Simple Interest in Maths?
- Simple Interest Formula Explained
- Simple Interest Formula for Years, Months & Days
- Simple Interest Examples & Practice Questions
- Conclusion
- Frequently Asked Questions (FAQs)
- Defining Mathematical Ratios
- Understanding Proportions Fundamentals
- Differentiating Ratios from Proportions
- Ratio and Proportion Formulas
- Properties of Ratio and Proportion
- How to Solve Ratio and Proportion Problems
- Ratio and Proportion Problems (With Solutions)
- Summary
- Frequently Asked Questions
- What is Number in Maths?
- Types of Numbers With Example
- Real vs Complex Numbers Explored
- Basic Operations on Numbers
- Practice Questions (With Solutions)
- Frequently Asked Questions
- What is Arithmetic Progression (AP) in Maths?
- Important Terminologies in Arithmetic Progression
- Basic Terms in Arithmetic Progression
- General Form Of Arithmetic Progression Series
- Types Of Arithmetic Progression
- Solved Questions With Explanation (MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
- Understanding Basic Concept
- Importance Of Train Problems In Aptitude
- Tips To Solve Train Problems
- Selected Practice Questions & Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Definition Of Mode
- Calculating Mode For Ungrouped Data
- Calculating Mode For Grouped Data
- Bimodal, Trimodal & Multimodal Distributions
- Comparing Mean, Median & Mode
- Selected Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Important Concept In Races And Games
- Calculating Time, Speed & Distance
- Importance Of Races And Games Problems
- Sample Practice Questions With Answers
- Conclusion
- Frequently Asked Questions (FAQs)
- Types Of Partnership
- Formula For Partnership Questions
- Tips To Solve Partnership Aptitude Questions
- Selected Partnership Questions (Practice MCQs)
- Conclusion
- Frequently Asked Questions (FAQs)
Decimal To Fraction Conversion Guide (+ Solved Questions)

Decimals and fractions are fundamental concepts in Mathematics. Understanding how to convert a decimal to fraction can simplify calculations and problem-solving, allowing for more versatility in mathematical operations.
Historically, decimal to fraction conversion dates back to ancient civilizations like the Egyptians and Babylonians, who used rudimentary methods for these conversions. Today, with modern mathematical principles, converting decimals to fractions is more straightforward and crucial for various academic and real-world applications.
All About Decimals

Definition: Decimals are numbers that include a decimal point, separating the whole number part from the fractional part. Decimals are used in measurement, currency, and mathematical calculations.
Significance: The decimal point indicates where the value transitions from an integer to a fraction. Unlike whole numbers, decimals allow for more precise values; providing a way to express values between whole numbers with accuracy.
Understanding decimal to fraction conversion is crucial for various real-world applications such as cooking recipes, measurements, and financial calculations. It enables individuals to work with fractions effectively and accurately in everyday scenarios.
Place Value Concept
In decimals, each digit's position carries a different weight based on its distance from the decimal point. This concept is known as place value and determines the digit's contribution to the overall value.
Understanding the placement of the decimal point is essential for correctly interpreting decimal numbers. Each digit's position after the decimal point represents a specific fraction of the whole value.
The place value system helps in understanding how each digit impacts the magnitude of the number. For example, in 0.25, the '2' represents two-tenths, while '5' signifies five hundredths.
All About Fractions
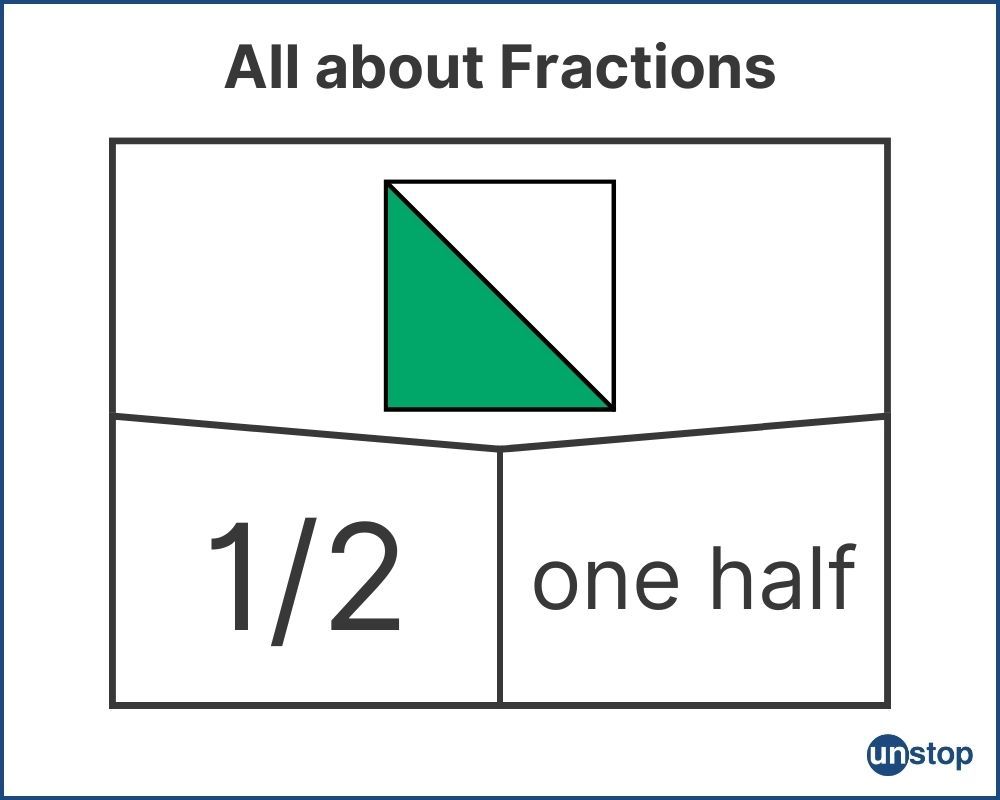
Fractions play a significant role in mathematics and are fundamental for various mathematical concepts and applications.
Fractions represent a way to express numbers that are not whole. A fraction consists of two parts: a numerator, which is the top number, and a denominator, which is the bottom number. The numerator represents the part of the whole, while the denominator shows how many equal parts the whole has been divided into.
Fractions are essential in various mathematical operations, such as addition, subtraction, multiplication, and division. Fractions also help in comparing quantities and understanding proportions.
How to Convert a Decimal into Fraction

In various everyday applications, understanding decimal to fraction conversion simplifies tasks. For example, when baking and a recipe calls for 0.5 cups of flour, knowing it's equivalent to 1/2 cup helps in precise measurement.
There are two main ways to convert a decimal to a fraction:
Method 1: Multiply by a power of 10
- Count the number of digits behind the decimal point.
- Multiply the decimal by 10 raised to the power of the number of digits behind the decimal point. This essentially moves the decimal point all the way to the right without changing the value.
- Write the resulting number as a fraction over the same denominator (10, 100, 1000, etc.)
Example: Convert 0.75 to a fraction
- There are two digits behind the decimal (7 and 5).
- Multiply 0.75 by 10² i.e. (10 x 10): 0.75 x 100 = 75
- Write 75 as a fraction over 100: 75/100
Method 2: Using place value
- Identify the place value of each digit after the decimal: Look at the digits behind the decimal point. The first digit represents tenths (1/10), the second digit represents hundredths (1/100), the third digit represents thousandths (1/1000), and so on.
- Write the decimal as a fraction: For each digit after the decimal point, write it as the numerator (top number) over its corresponding place value (denominator).
- Combine the fractions: If there are multiple digits after the decimal, you can often combine them into a single fraction by adding the individual fractions together.
- Simplify the fraction (optional): See if the numerator and denominator have any common factors you can divide by to get a simpler fraction. Finding the HCF (Highest Common Factor) is an optional step, but it's a helpful way to express the final answer in its most reduced form.
Example: Convert 0.75 to a fraction.
- 0.7 = seven tenths = 7/10
- 0.05 = five hundredths = 5/100
- Since there are multiple digits after the decimal, we can combine them: 7/10 + 5/100
- Simplifying the combined fraction: (7 x 10 + 5) / (100) = 75/100
- Simplify the fraction further by dividing both numerator and denominator by their GCF - divide 75 and 100 by their GCF, which is 25, resulting in 3/4.
Remember: Both methods will give you the same equivalent fraction. Choose whichever method you find easier to understand and apply.
Handling Negative Decimals
- To convert negative decimals to fractions, start by removing the negative sign. Treat the number as positive before converting it to a fraction.
- After removing the negative sign, proceed with converting the decimal to a fraction using standard methods.
- Once you have the fraction, reapply the negative sign to the numerator or denominator, not both.
Misconceptions Clarified: One common misconception is that when dealing with negative decimals, both the numerator and denominator should be negative in the fraction. This is incorrect. Only one of them should carry the negative sign.
Example of Negative Decimal: Convert -0.75 to a fraction
- Remove the negative sign: 0.75.
- Convert 0.75 to a fraction: 3/4.
- Reapply the negative sign either to the numerator (-3/4) or denominator (3/-4).
Simple vs Recurring Decimals

What are Simple Decimals?
Simple decimals are a type of decimal number that does not repeat or have a pattern in the digits after the decimal point. These decimals are finite and can be easily expressed as a fraction.
For example, 0.3 is a simple decimal because it ends after two digits and can be written as 3/10 in fraction form. Simple decimals are straightforward to work with in mathematical calculations and conversions.
Converting Simple Decimals to Fractions
To convert simple decimals to fractions, identify the decimal places. For example, in 0.5, there is one decimal place. Next, consider the digits after the decimal point when converting. In 0.25, there are two digits after the decimal point.
Take the digits after the decimal point as the numerator. The denominator is based on the number of decimal places. Reduce the fraction if possible for simplicity.
Example:
- Decimal: 0.3
- Digits: One digit after the decimal point
- Conversion: 3/10
What are Recurring Decimals?
Recurring decimals are numbers that have a repeating pattern of digits after the decimal point. This pattern can be a single digit, a group of digits, or even alternate digits that repeat indefinitely. For example, 0.3333... is a recurring decimal where the digit 3 repeats infinitely.
Recurring decimals can be identified by noticing the repetition of certain digits or groups of digits in the decimal representation of a number. Repeating decimals, like 0.333..., can be challenging to convert directly. By identifying the repeating pattern, we can simplify the conversion process.
Converting recurring decimals to fractions involves a bit more manipulation compared to simple decimals. Let’s study the process in detail:
Converting Recurring Decimals to Fractions
Here's a step-by-step approach to converting recurring decimals to fractions:
- Identify the Repeating Part: Look for the digit(s) that repeat endlessly after the decimal point.
- Set up two equations:
- Let x represent the entire decimal you want to convert to a fraction.
- Write two equations where the digits after the decimal point are identical:
- Equation 1: Assign the value of x to the decimal.
- Equation 2: Move the decimal point in Equation 1 one or more places to the right, so the ENTIRE repeating block is included. The number of places you move the decimal will depend on the number of digits in the repeating block.
- Subtract the equations: Subtract the second equation (with the moved decimal) from the first equation. This essentially cancels out the digits before the decimal point and isolates the repeating part.
- Solve for x: Inthe resulting equation, the repeating part is gone.Now you can solve for x by dividing both sides by the number you multiplied by in step 2 (the number you moved the decimal by).
- Simplify the fraction (optional): See if the numerator and denominator have any common factors you can divide by to get a simpler fraction.
Example: Let’s take a look at the recurring decimal 0.414141… to understand the steps
- Identify the repeating part: The repeating part is "41" (clearly visible in the decimal).
- Set up two equations:
- Let x represent the decimal (x = 0.414141...).
- Create a second equation where the decimal point is moved two places to the right (since the repeating block has two digits). This ensures the entire repeating part is captured:
- 100x = 41.4141..
- Subtract the equations: Now, subtract the first equation (x) from the second equation (100x). This cancels out the digits before the decimal point and isolates the repeating part:
- 100x - x = (41.4141...) - (0.4141...)
- 99x = 41
- Solve for x: Divide both sides by 99 (the number you multiplied by in step 2):
- x = 41 / 99
- Simplify the fraction (optional): The numerator and denominator don't have any common factors (besides 1), so the fraction is already in its most reduced form. Therefore, x = 41/99.
Explanation:
- Moving the decimal point in the second equation by two places is the same as multiplying by 100 (10 x 10). This creates a denominator (100) large enough to hold the entire repeating block when we subtract the equations.
- Subtracting the equations essentially removes the non-repeating part (the "0.") from both sides, leaving only the repeating part ("41").
- Dividing by 99 gets rid of the extra multiplication by 100 and isolates x.
- Therefore, 0.414141... is equivalent to the fraction 41/99.
Remember! Accurately identifying and handling repeating patterns is crucial for precision in converting decimals to fractions. A small oversight can lead to incorrect results.
Conversion Charts
Different tools can be used to convert decimal to fraction, with calculators being the most common. Apart from calculators, conversion charts are also popular.
Conversion charts offer a visual representation of decimal to fraction conversions, aiding in better comprehension. These charts typically display common decimal values alongside their corresponding fractional equivalents for quick reference.
Here's an example of a basic conversion chart for decimals to fractions:
| Decimal Places | Fraction |
|---|---|
| 0 | 1/1 |
| 0.1 | 1/10 |
| 0.01 | 1/100 |
| 0.001 | 1/1000 |
| 0.25 | 1/4 |
| 0.5 | 1/2 |
| 0.75 | 3/4 |
| 0.222... | 2/9 |
| 0.83333333 | 5/6 |
| 1.8 | 9/5 |
Pros and Cons of Conversion Charts
Conversion charts are a helpful tool, but they shouldn't replace understanding the underlying concepts of place value and fraction conversion.
| Benefits | Limitations |
|---|---|
| Quick and easy: Conversion charts are a fast way to find common fraction equivalents without needing to perform calculations. | Limited scope: Conversion charts typically only show a limited set of common decimals and their fractions. They may not cover every possible decimal value. |
| Helpful for beginners: They can be a valuable resource for people who are still learning about place value and converting between decimals and fractions. | Accuracy for repeating decimals: Charts usually don't show fractions for repeating decimals, which require a different conversion process. |
Practice Questions (With Solutions)
Q1. Write 0.625 as a fraction.
Options:
a) 5/3
b) 11/7
c) 9/14
d) 5/8
Answer: d) 5/8
Solution Explained
Here's how we can convert the decimal 0.625 to a fraction:
- Denominator based on decimal places: There are three digits (6,2 and 5) after the decimal point in 0.625. The denominator of the fraction will be 10 raised to the power of the number of decimal places (3) - 10³ (10 x 10 x 10). So, we have an initial fraction of 625/1000.
- Simplification: The numerator (625) and denominator (1000) share a common divisor of 125. Dividing both the numerator and denominator by 125 gives us:
- 625/100 = (625/125) / (1000 /125) = 5/8.
- Therefore, 0.625 expressed as a fraction in its lowest terms is 5/8.
Q2. Convert 0.75 to a fraction.
Options:
a) 3/4
b) 1/2
c) 3/5
d) 7/8
Answer: a) 3/4
Solution Explained
Here's how we can convert the decimal 0.75 to a fraction:
- Denominator based on decimal places: There are two digits (7 and 5) after the decimal point in 0.75. The denominator of the fraction will be 10 raised to the power of the number of decimal places (10² or 10 x 10). So, we have an initial fraction of 75/100.
- Simplification: The numerator (75) and denominator (100) share a common divisor of 25. Dividing both the numerator and denominator by 25 gives us:
- 75/100 = (75 / 25) / (100 / 25) = 3/4
- Therefore, 0.75 expressed as a fraction in its lowest terms is 3/4.
Q3. Express 0.36 as a fraction.
Options:
a) 7/20
b) 4/11
c) 5/16
d) 9/25
Answer: d) 9/25
Solution Explained
Here's how we can convert the decimal 0.36 to a fraction:
- Denominator based on decimal places: There are two digits (3 and 6) after the decimal point in 0.36. The denominator of the fraction will be 10 raised to the power of the number of decimal places (10² or 10 x 10). So, we have an initial fraction of 36/100.
- Simplification: The numerator (36) and denominator (100) share a common divisor of 4. Dividing both the numerator and denominator by 4 gives us:
- 36/100 = (36 / 4) / (100 / 4) = 9 / 25
- Therefore, 0.36 expressed as a fraction in its lowest terms is 9/25.
Q4. Write 0.008 as a fraction.
Options:
a) 10/11
b) 1/125
c) 7/25
d) 12/51
Answer: b) 1/125
Solution Explained
Here’s how to solve it:
- Denominator based on decimal places: There are three digits (0, 0, and 8) after the decimal point in 0.008. The denominator of the fraction will be 10 raised to the power of the number of decimal places (3) -10³ (10 x 10 x 10). This gives us the initial fraction 8/1000.
- Simplification: We can simplify the fraction 8/1000 by finding the greatest common divisor (GCD) of the numerator (8) and denominator (1000). The GCD of 8 and 1000 is 8. Dividing both the numerator and denominator by 8 gives us:
- 8 / 1000 = (8 / 8) / (1000 / 8) = 1 / 125
- Therefore, 0.008 expressed as a fraction in its lowest terms is 1/125.
Q6. Convert 0.125 to a fraction.
Options:
a) 3/5
b) 5/7
c) 1/8
d) 1/6
Answer: c) 1/8
Solution Explained
Here's how to solve it:
- Denominator based on decimal places: There are three digits (1, 2, and 5) after the decimal point in 0.125. The denominator of the fraction will be 10 raised to the power of the number of decimal places (3) -10³ (10 x 10 x 10). This gives us the initial fraction 125/1000.
- Simplification: This can be simplified using the greatest common divisor (GCD). GCD of 125 and 1000 is 125. Dividing both the numerator and denominator by 125 gives us:
- 125/1000 = (125 / 125) / (1000 / 125) = 1/8
- Therefore, 0.125 expressed as a fraction in its simplest form is 1/8.
Q7. What is the fraction equivalent of the recurring decimal 0.373737...?
Options:
a) 37/99
b) 37/100
c) 37/98
d) 11/29
Answer: a) 37/99
Solution Explained
Here's how to solve it:
- Let x represent the decimal: x = 0.373737...
- We will manipulate the decimal to isolate the repeating part. Since the decimal repeats every two digits, let's consider two equations:
- One equation where we capture the entire decimal (x).
- Another equation where we move the decimal point two places to the right (effectively multiplying by 100). This captures only the repeating block.
- New equation: 100 * x = 37.3737...
- Now, subtract the original equation (x) from the new equation: (100 * x) - x = (37.3737...) - (0.3737...)
- This subtraction eliminates all digits before the decimal point and keeps repeating digits because they cancel out when subtracted from themselves.
- Simplifying the equation: 99x = 37
- Solve for x by dividing both sides by 99: x = 37 / 99
- Therefore, the repeating decimal 0.373737... is equivalent to the fraction 37/99.
Q8. Express the decimal 0.1625 as a fraction in simplest form.
Options:
a) 4/25
b) 5/24
c) 13/80
d) 8/39
Answer: c) 13/80
Solution Explained
Here's how to convert it:
- Denominator based on decimal places: There are four digits (1, 6, 2, and 5) after the decimal point. The denominator of the fraction will be 10 raised to the power of the number of decimal places (4) - 10⁴ (10 x 10 x 10 x 10). This gives us the initial fraction 1625/10000.
- Simplify the fraction: The numerator (1625) and denominator (10000) share a common divisor of 125. Dividing both the numerator and denominator by 125 gives us:
- 1625 / 1000 = (1625 /125) / (1000 /125) = 13 / 80
- Therefore, 0.1625 expressed as a fraction in its simplest form is 13/80.
Q9. Convert the decimal 0.8642 to a fraction in its lowest terms.
Options:
a) 432/625
b) 4321/5000
c) 54/625
d) 432/5000
Answer: b) 4321/5000
Solution Explained
Here’s how to solve it:
- Denominator based on decimal places: There are four digits (8, 6, 4, and 2) after the decimal point. The denominator of the fraction will be 10 raised to the power of the number of decimal places (4) - 10⁴ (10 x 10 x 10 x 10). This gives us the initial fraction 8642/10000.
- Simplification: We can further simplify the fraction by finding the greatest common divisor (GCD) of the numerator (8642) and denominator (10000). The GCD of 8642 and 10000 is 2. Dividing both the numerator and denominator by 2 gives us:
- (8642 / 2) / (10000 / 2) = 4321 / 5000
- The GCD of 4321 and 5000 is 1. Therefore, the fraction is already in its lowest terms.
- 0.8642 expressed as a fraction in its lowest terms is 4321/5000.
Q10. What fraction represents the repeating decimal 0.142857142857...?
Options:
a) 1/7
b) 1/6
c) 1/9
d) 1/11
Answer: a) 1/7
Solution Explained
Here's how to solve it:
- Let x represent the decimal: x = 0.142857142857...
- We will manipulate the decimal to isolate the repeating part. Since the decimal repeats every 6 digits, let's consider two equations:
- One equation where we capture the entire decimal (x).
- Another equation where we move the decimal point six places to the right (effectively multiplying by 10^6). This captures only the repeating block.
- New equation: 10^6 * x = 142857.142857...
- Now, subtract the original equation (x) from the new equation:
- (10^6 * x) - x = (142857.142857...) - (0.142857142857...)
- This subtraction eliminates all digits before the decimal point and keeps repeating digits because they cancel out when subtracted from themselves.
- Simplifying the equation: 999999x = 142857
- Solve for x by dividing both sides by 999999: x = 142857 / 999999
- x = 1/7 (greatest common divisor of 142857 and 999999 is 1)
- Therefore, the repeating decimal 0.142857142857... is equivalent to the fraction 1/7.
Q11. Express the decimal 0.575 as a fraction in simplest form.
Options:
a) 115/200
b) 23/50
c) 23/40
d) 23/80
Answer: c) 23/40
Solution Explained
Here’s how to solve it:
- Denominator based on decimal places: There are three digits (5,7 and 5) after the decimal point in 0.575. The denominator of the fraction will be 10 raised to the power of the number of decimal places (3). So, we have 0.575 = 575/1000.
- Simplify: The fraction 575/1000 can be simplified by finding the greatest common divisor (GCD) of 575 and 1000. The GCD is 25.
- Dividing both the numerator and denominator by 25 gives us 23/40.
Learn more about decimal to fraction and other topics covered under Quantitative Aptitude here and amp up your preparation.
Closing Thoughts
Understanding the basics of decimal to fraction conversion, utilizing conversion tools, and following step-by-step processes will enable you to handle any decimal conversion effortlessly. Remember, practice makes perfect, so keep honing your skills through additional resources and references. The more you practice, the more proficient you will become in this essential mathematical skill!
Time For A Short Quiz
Frequently Asked Questions
1. How do I convert a decimal to a fraction?
To convert a decimal to a fraction, write the decimal as a fraction with the decimal number as the numerator and a power of 10 as the denominator.
2. What tools are available for decimal conversion?
Various online tools and calculators are available to help you convert decimals to fractions quickly and accurately. You can also refer to conversion charts that list common decimal to fraction conversions. These tools simplify the conversion process and provide instant results, saving you time and effort.
3. How do I simplify a fraction obtained from a decimal conversion?
To simplify a fraction, find the greatest common divisor (GCD) or the HCF (Highest Common Factor) of the numerator and denominator, and divide both by this common divisor.
4. How do I convert a repeating decimal to a fraction?
To convert a repeating decimal to a fraction, identify the repeating pattern, set up an equation to subtract the non-repeating part from the entire decimal, and solve for the fraction using algebra.
5. Can all decimals be converted to fractions?
No, not all decimals can be converted to fractions. Terminating (simple) decimals and repeating decimals with a single repeating pattern can be converted to fractions, but decimals that neither terminate nor repeat cannot be expressed as fractions.
7. How do I know if a decimal can be represented as a fraction in simplest form?
A decimal can be represented as a fraction in simplest form if the numerator and denominator have no common factors other than 1.
8. What are some common mistakes to avoid when converting decimals to fractions?
One common mistake is forgetting to simplify the fraction after conversion. Additionally, misidentifying the repeating pattern in a repeating decimal or making errors in long division can lead to inaccuracies. It's important to double-check the conversion and simplify the fraction if necessary.
9. Are there any real-world applications where converting decimals to fractions is useful?
Converting decimals to fractions is useful in various real-world scenarios, such as in finance for calculating interest rates, in construction for measuring dimensions, in cooking for adjusting recipe proportions, and in engineering for precise measurements. Fractional representations are often more intuitive and practical than decimals in these contexts.
10. What are some common misconceptions about converting decimals to fractions?
One common misconception is that all decimals can be easily converted to fractions. In reality, only terminating decimals and repeating decimals can be expressed as fractions.
Another misconception is that decimals are always more accurate than fractions, whereas fractions can sometimes provide more precise representations, especially in certain mathematical calculations or practical applications.
Suggested Reads:
- Time, Speed And Distance- Formula With Aptitude Question & Answer
- Simplification- Basic Formulas With Practice Questions & Answers
- Height And Distance- Trigonometry Basics With Question & Answer
- What Is Mensuration: Formulas With Top Selected Question & Answer
- Mixture And Alligation: Explained With Selected Question & Answer
I’m a reader first and a writer second, constantly diving into the world of content. If I’m not writing or reading, I like watching movies and dreaming of a life by the beach.
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter
















Comments
Add comment