Prime Number Program In C | 12 Ways & Complexity Analysis (+Codes)

Prime numbers are numbers greater than 1 with only two divisors, i.e., 1 and the number itself, like 2, 3, 5, 7, 11, etc. They are significant for various purposes in the fields of mathematics, computer science, encryption techniques, and data compression algorithms.

In this article, we will discuss and understand different ways to write and run a prime number program in C language. We will start by understanding the concept of prime numbers first and then explore a fundamental algorithm. We will then go through different approaches and code examples, discuss optimization techniques, and analyze the time complexities of all the examples.

What Is A Prime Number?

As mentioned, a prime number is an integer greater than 1 that cannot be evenly divided by any other positive integer except for 1 and itself. For instance, 2, 3, 5, and 7. This divisibility is a distinct characteristic of prime numbers that sets them apart from others in the numerical landscape. Take, for example, the number 5, a prime number indivisible by any other integers except 1 and 5. That is, it does not have positive divisors beyond these two numbers.

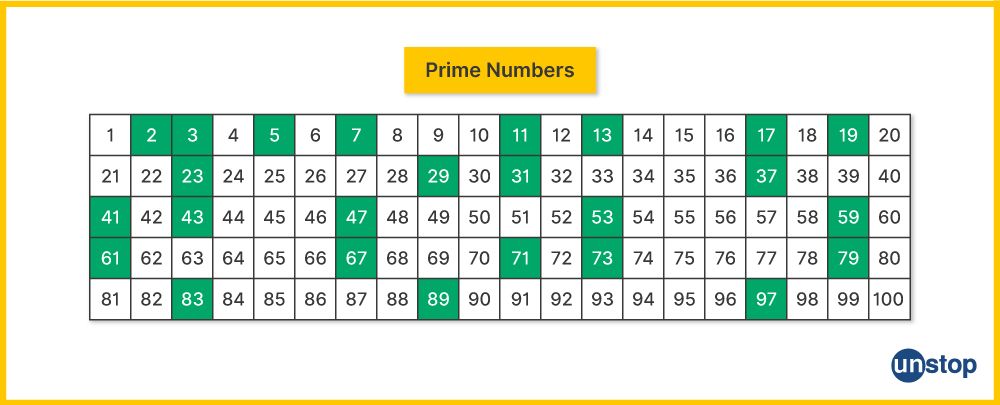
The following diagrammatic illustration shows the prime numbers between 1 and 100.

Algorithm For The Prime Number Program In C

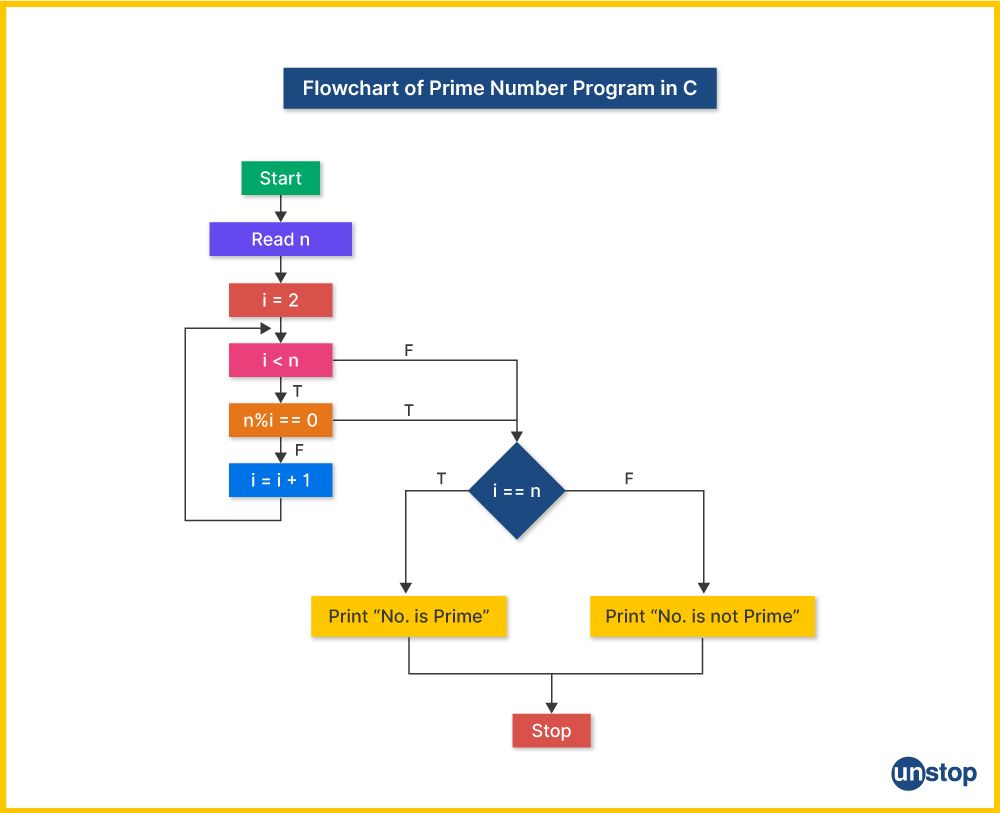
Determining whether a given number is a prime number involves checking its divisibility by other numbers. The key insight is that a prime number is only divisible by 1 and itself. Below is the basic approach/ algorithm you must follow to write and implement a prime number program in C programming language.

Step 1- Input: Prompt the user to input a range of numbers (start and end) or a single positive integer to check for primality.

Step 2- Iteration (For Loop): Iterate through each number in the given range or the single number. For this, we can use a for loop that starts from the first number in the range or the given number and continues until the last number in the range or the given number.

Step 3- Prime Check (In Iteration): For each number in the range (i.e., during each iteration), perform the following steps:

1. Handle special cases:

• If the number is less than or equal to 1, it's not prime. Move to the next number.
• If the number is 2, it's prime. Print it and move to the next number.
• If the number is even (except 2), it's not prime. Move to the next number.

2. For odd numbers greater than 2:

• Check divisibility by all odd numbers from 3 up to the square root of the number.
• If the number is divisible by any of these divisors, it's not prime. Move to the next number.

Step 4- Output: If a number is determined to be prime based on the above steps, print it. Repeat this process for each number in the range or the single number.

Prime Number Program In C Using Naive Approach

In the naive approach to checking for prime numbers, we use a function that first checks if the number is less than 2. Since numbers less than 2 are not prime, the program must return false in such cases. If the condition is not true, then the function moves to iterate through all numbers from 2 to n-1, checking if the number is divisible by any of them. If a divisor is found, it indicates that the respective number is not prime, returning false. If no divisor is found within this range, the conclusion is that the number is prime thus returning true.

Pseudocode of Naive Approach to Write a Prime Number Program in C Language:

Function isPrimeNaive(n):
// Base case: numbers less than 2 are not prime
If n < 2 Then
Return false

// Check divisibility from 2 to n-1
For i from 2 to n-1:
If n % i == 0 Then
Return false // Not a prime number

// If no divisor is found, the number is prime
Return true

In the pseudocode above, we have defined a function that checks for a prime number by iterating through the range and cross-checking for specific conditions. Look at the simple C program below to understand how this can be implemented in C code.

Code Example:

I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRib29sLmg+CgovLyBGdW5jdGlvbiB0byBjaGVjayBpZiBhIG51bWJlciBpcyBwcmltZSB1c2luZyBhIG5haXZlIGFwcHJvYWNoCmJvb2wgaXNQcmltZU5haXZlKGludCBuKSB7Ci8vIEJhc2UgY2FzZTogbnVtYmVycyBsZXNzIHRoYW4gMiBhcmUgbm90IHByaW1lCmlmIChuIDwgMikKcmV0dXJuIGZhbHNlOwoKLy8gQ2hlY2sgZGl2aXNpYmlsaXR5IGZyb20gMiB0byBuLTEKZm9yIChpbnQgaSA9IDI7IGkgPCBuOyBpKyspIHsKaWYgKG4gJSBpID09IDApCnJldHVybiBmYWxzZTsgLy8gTm90IGEgcHJpbWUgbnVtYmVyCn0KLy8gSWYgbm8gZGl2aXNvciBpcyBmb3VuZCwgdGhlIG51bWJlciBpcyBwcmltZQpyZXR1cm4gdHJ1ZTsKfQoKaW50IG1haW4oKSB7CmludCBudW1iZXI7CgpwcmludGYoIkVudGVyIGEgbnVtYmVyOiAiKTsKc2NhbmYoIiVkIiwgJm51bWJlcik7CgovLyBDaGVjayBpZiB0aGUgbnVtYmVyIGlzIHByaW1lCmlmIChpc1ByaW1lTmFpdmUobnVtYmVyKSkKcHJpbnRmKCIlZCBpcyBhIHByaW1lIG51bWJlci5cbiIsIG51bWJlcik7CmVsc2UKcHJpbnRmKCIlZCBpcyBub3QgYSBwcmltZSBudW1iZXIuXG4iLCBudW1iZXIpOwovLyBSZXR1cm4gMCB0byBpbmRpY2F0ZSBzdWNjZXNzZnVsIGV4ZWN1dGlvbgoKcmV0dXJuIDA7Cn0=

Output:

Enter a number: 5
5 is a prime number.

Explanation:

In the sample C code, we begin by importing the essential header files, i.e., <stdio.h> and <stdbool.h> for input-output operations and Boolean data type, respectively.

1. We then define a function called isPrimeNaive(), which takes an integer n as input and returns a boolean value indicating whether n is prime or not.
2. As mentioned in the code comment, the function uses a naive approach by checking divisibility from 2 to n-1. Inside the function-
   • We use an if-statement to first check if n is less than 2. If the condition is true, i.e., n<2, the function returns false since numbers less than 2 are not prime.
   • If the condition is false, we use a for-loop to iterate the range of numbers from 2 to n-1.
   • The loop construct begins with loop variable i=2 and continues till i<n (loop condition), with the value i being incremented by 1 after every iteration.
   • We have another if-statement inside the loop, which checks if n is divisible by the i using the modulo arithmetic operator and the equality relational operator. 
   • If the condition is true, the loop returns false, indicating that n is not prime.
   • If the loop completes without finding any divisor that evenly divides n, it returns true, indicating that n is prime.
3. In the main() function, we declare an integer data type variable called number to store the user input.
4. Next, we use the printf() function to prompt the user to input a value for number, read the value using the scanf() function and store it in the respective variable using the address-of operator (&).
5. After that, we use an if-else statement where we call the isPrimeNaive() function by passing the number variable as an argument. 
6. If the function returns true, the if-block is executed, and the printf() statement displays the string message indicating that the number is prime.
7. If the function returns false, the else block is executed, printing that the number is not prime.
8. The %d format specifier in the printf() statements is the placeholder for an integer value, and the newline escape sequence is used to shift the cursor to the next line. 
9. Finally, the main() function terminates with a return 0 statement, indicating successful execution.

Time Complexity: O(n)
Space Complexity: O(1)

Prime Number Program In C Using sqrt(N) Approach

The sqrt(N) approach is an optimization of the naive method of writing a prime number program in C. We use the square root function from the <math.h> module in the C library to check for prime numbers as follows:

• We define a function, say, isPrimeSqrt, which first handles special cases: if the number is less than 2, it returns false, and if the number is 2, it returns true, as 2 is a prime number.
• Then, it iterates through potential divisors from 2 up to the square root of the input number.
• If the number is divisible by any of these divisors, the function returns false, indicating that the number is not prime.
• If no divisor is found within this range, the function concludes that the number is prime and returns true.

Look at the C program sample below to understand how this approach to writing a prime number program materializes in C language.

Code Example:

I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRib29sLmg+CiNpbmNsdWRlIDxtYXRoLmg+CgovLyBGdW5jdGlvbiB0byBjaGVjayBpZiBhIG51bWJlciBpcyBwcmltZSB1c2luZyB0aGUgc3F1YXJlIHJvb3QgYXBwcm9hY2gKYm9vbCBpc1ByaW1lU3FydChpbnQgbikgewovLyBCYXNlIGNhc2U6IG51bWJlcnMgbGVzcyB0aGFuIDIgYXJlIG5vdCBwcmltZQppZiAobiA8IDIpCnJldHVybiBmYWxzZTsKCi8vIFNwZWNpYWwgY2FzZTogMiBpcyBhIHByaW1lIG51bWJlcgppZiAobiA9PSAyKQpyZXR1cm4gdHJ1ZTsKCi8vIENoZWNrIGRpdmlzaWJpbGl0eSBmcm9tIDIgdG8gc3F1YXJlIHJvb3Qgb2Ygbgpmb3IgKGludCBpID0gMjsgaSA8PSBzcXJ0KG4pOyBpKyspIHsKaWYgKG4gJSBpID09IDApCnJldHVybiBmYWxzZTsgLy8gTm90IGEgcHJpbWUgbnVtYmVyCn0KLy8gSWYgbm8gZGl2aXNvciBpcyBmb3VuZCwgdGhlIG51bWJlciBpcyBwcmltZQpyZXR1cm4gdHJ1ZTsKfQoKaW50IG1haW4oKSB7CgppbnQgbnVtYmVyOwpwcmludGYoIkVudGVyIGEgbnVtYmVyOiAiKTsKc2NhbmYoIiVkIiwgJm51bWJlcik7CgovLyBDaGVjayBpZiB0aGUgbnVtYmVyIGlzIHByaW1lCmlmIChpc1ByaW1lU3FydChudW1iZXIpKQpwcmludGYoIiVkIGlzIGEgcHJpbWUgbnVtYmVyLlxuIiwgbnVtYmVyKTsKZWxzZQpwcmludGYoIiVkIGlzIG5vdCBhIHByaW1lIG51bWJlci5cbiIsIG51bWJlcik7CgovLyBSZXR1cm4gMCB0byBpbmRpY2F0ZSBzdWNjZXNzZnVsIGV4ZWN1dGlvbgpyZXR1cm4gMDsKfQ==

Output:

Enter a number: 1
1 is not a prime number.

Explanation:

In the C code sample-

1. We define a function called isPrimeSqrt(), which takes an integer n as input and returns a boolean value indicating whether n is prime or not.
2. This function uses an optimization by checking divisibility only up to the square root of n as follows-
   • We use an if-statement to check if n is less than 2, i.e., n<2. If it is, we immediately return false, indicating that numbers less than 2 are not prime.
   • Using another if-statement, we check if n is equal to 2, i.e., n==2. If it is, we return true since 2 is a prime number.
   • If none of the base checks are satisfied, we move to the for loop construct to iterate through the range of numbers from 2 to the square root of n (upper limit).
   • That is, the loop begins with i=2 and continues until the loop condition, i.e., i<=sqrt(n), is satisfied. We use the sqrt() function from the math module here.
   • In every loop iteration, we check if n is divisible by i (leaves no remainder). If it is, we return false, indicating that n is not prime.
   • If the loop completes without finding any divisor that evenly divides n, we return true, indicating that n is prime.
3. In the main() function, we declare an integer variable number and prompt the user to provide a value for this variable using printf() and scanf() functions.
4. Next, we call the isPrimeSrt() function inside an if-else statement by passing the number as an argument. 
5. If the function returns true, the if-block prints a string message indicating that the number is prime.
6. If the function returns false, the else-block prints a message indicating the same.
7. Finally, the program returns 0 to indicate successful execution without any errors.

Time Complexity: O(sqrt(n))
Space Complexity: O(1) 

Prime Number Program In C Using Most Efficient sqrt(N)

We have already discussed the naive approach to check for prime numbers, followed by an optimized version using the sqrt() function. We can further optimize the approach to defining a few more cases with better conditions. In this approach to writing a prime number program in C language-

• We first determine whether the input number is less than two, in which case the number is not prime.
• In the next case, we check if it is 2 or 3, which we directly declare as a prime number.
• For the remaining numbers we begin iterating from the range of 5 to the square root of the number, looking for potential divisors, skipping multiples of 2 and 3. This lowers the number of checks even more, increasing the algorithm's efficiency. 

The C program example below showcases how this approach to writing the most efficient prime number program in C is implemented. 

Code Example:

I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRib29sLmg+CiNpbmNsdWRlIDxtYXRoLmg+CgovLyBGdW5jdGlvbiB0byBjaGVjayBpZiBhIG51bWJlciBpcyBwcmltZSB1c2luZyBhbiBlZmZpY2llbnQgYXBwcm9hY2gKYm9vbCBpc1ByaW1lRWZmaWNpZW50KGludCBuKSB7Ci8vIEJhc2UgY2FzZTogbnVtYmVycyBsZXNzIHRoYW4gMiBhcmUgbm90IHByaW1lCmlmIChuIDwgMikKcmV0dXJuIGZhbHNlOwoKLy8gU3BlY2lhbCBjYXNlczogMiBhbmQgMyBhcmUgcHJpbWUgbnVtYmVycwppZiAobiA9PSAyIHx8IG4gPT0gMykKcmV0dXJuIHRydWU7CgovLyBDaGVjayBkaXZpc2liaWxpdHkgYnkgMiBhbmQgMwppZiAobiAlIDIgPT0gMCB8fCBuICUgMyA9PSAwKQpyZXR1cm4gZmFsc2U7CgovLyBDaGVjayBkaXZpc2liaWxpdHkgZm9yIG51bWJlcnMgb2YgdGhlIGZvcm0gNmsgwrEgMQpmb3IgKGludCBpID0gNTsgaSAqIGkgPD0gbjsgaSArPSA2KSB7CmlmIChuICUgaSA9PSAwIHx8IG4gJSAoaSArIDIpID09IDApCnJldHVybiBmYWxzZTsgLy8gTm90IGEgcHJpbWUgbnVtYmVyCn0KcmV0dXJuIHRydWU7IC8vIElmIG5vIGRpdmlzb3IgaXMgZm91bmQsIHRoZSBudW1iZXIgaXMgcHJpbWUKfQoKaW50IG1haW4oKSB7CmludCBudW1iZXI7CnByaW50ZigiRW50ZXIgYSBudW1iZXI6ICIpOwpzY2FuZigiJWQiLCAmbnVtYmVyKTsKCi8vIENoZWNrIGlmIHRoZSBudW1iZXIgaXMgcHJpbWUKaWYgKGlzUHJpbWVFZmZpY2llbnQobnVtYmVyKSkKcHJpbnRmKCIlZCBpcyBhIHByaW1lIG51bWJlci5cbiIsIG51bWJlcik7CmVsc2UKcHJpbnRmKCIlZCBpcyBub3QgYSBwcmltZSBudW1iZXIuXG4iLCBudW1iZXIpOwoKcmV0dXJuIDA7Cn0=

Output:

Enter a number: 23
23 is a prime number.

Explanation:

In the C code example- 

1. We begin by defining a function isPrimeEfficient(), which takes an integer n as input and returns a boolean value indicating whether n is prime or not.
2. This function uses an efficient approach to check for primality. Inside the function-
   • We use an if-statement to check if n is less than 2. If it is, we immediately return false, indicating that numbers less than 2 are not prime.
   • If the previous statement returns true, we check if n is equal to 2 or 3 using another if-statement. If it is, we return true since 2 and 3 are prime numbers.
   • If none of the base checks are met, we check if n is divisible by 2 or 3. If it is, we return false since no number greater than 3 and divisible by 2 or 3 can be prime.
   • In case all the previous statements return true, the program control moves to a for loop that starts from 5 and iterates as long as the square root of i is less than or equal to n.
   • Note that we increment the value of i by 6 in every iteration using the compound addition assignment operator.
   • Inside the loop, we check if n is divisible by i or i + 2 (connecting the conditions using the logical AND operator) since numbers of form 6k ± 1 are potential factors of prime numbers.
   • If the condition is true, the function returns false, indicating that n is not prime.
   • If the loop completes without finding any divisor that evenly divides n, we return true, indicating that n is prime.
3. In the main() function, we declare an integer variable number and prompt the user to provide a value for the same.
4. Next, we check if the input number is prime by calling the isPrimeEfficient() function with the number as an argument inside an if-else statement.
5. If the function returns true, we print that the number is prime.
6. If the function returns false, we print that the number is not prime.
7. In this example, we have taken the input value 23, which is a prime number as shown in the output window.

Time Complexity: O(sqrt(n))
Space Complexity: O(1)

Wilson Theorem To Write A Prime Number Program In C

Wilson's Theorem offers an interesting method for finding prime integers. Number theory gives the origin of Wilson's Theorem, which offers a standard to judge if a particular number is prime. The theorem states that a natural number p>1 is a prime number if and only if (p−1)!≡−1(mod p), where ≡ denotes congruence.

In simple words, if (p - 1)! + 1 is divisible by p, then n is a prime number. Below is a brief explanation of how to write and run program to find prime number in C using this theorem.

• Wilson's Theorem states that a number p is prime if and only if (p-1)! ≡ -1 (mod p).
• Check if (num-1)! + 1 is divisible by num.
• If it is, then num is prime.
• If not, then num is not a prime number.

Note that while this approach is conceptually interesting, it is not the most efficient or practical for large numbers. This is because the computation of factorials can be expensive, and the time complexity can be high depending on the method used to compute factorials. The example C program below showcases how this approach can be implemented.

Code Example:

I2luY2x1ZGUgPHN0ZGlvLmg+CgppbnQgaXNQcmltZVdpbHNvbihpbnQgcCkgewovLyBCYXNlIGNhc2U6IDAgYW5kIDEgYXJlIG5vdCBwcmltZQppZiAocCA8PSAxKQpyZXR1cm4gMDsKCmludCBmYWN0b3JpYWxNb2RQID0gMTsKLy8gQ2FsY3VsYXRlIChwLTEpISAlIHAKZm9yIChpbnQgaSA9IDE7IGkgPD0gcCAtIDE7IGkrKykgewpmYWN0b3JpYWxNb2RQID0gKGZhY3RvcmlhbE1vZFAgKiBpKSAlIHA7Cn0KLy8gQ2hlY2sgaWYgKHAtMSkhIGlzIGNvbmdydWVudCB0byAtMSBtb2R1bG8gcApyZXR1cm4gKGZhY3RvcmlhbE1vZFAgPT0gcCAtIDEpOwp9CgppbnQgbWFpbigpIHsKaW50IG51bWJlcjsKcHJpbnRmKCJFbnRlciBhIG51bWJlcjogIik7CnNjYW5mKCIlZCIsICZudW1iZXIpOwoKLy8gQ2hlY2sgaWYgdGhlIG51bWJlciBpcyBwcmltZSB1c2luZyBXaWxzb24ncyBUaGVvcmVtCmlmIChpc1ByaW1lV2lsc29uKG51bWJlcikpCnByaW50ZigiJWQgaXMgYSBwcmltZSBudW1iZXIuXG4iLCBudW1iZXIpOwplbHNlCnByaW50ZigiJWQgaXMgbm90IGEgcHJpbWUgbnVtYmVyLlxuIiwgbnVtYmVyKTsKCnJldHVybiAwOwp9

Output:

Enter a number: 79
79 is a prime number.

Explanation:

In the example C code-

1. We define a function called isPrimeWilson(), which takes an integer p as input and returns an integer value indicating whether p is prime according to Wilson's Theorem. Inside the function-
   • We first check if p is less than or equal to 1. If it is, we return 0, indicating that 0 and 1 are not prime.
   • If the base case is not met, we initialize a variable factorialModP to 1, which will store the value of (p-1)! % p.
   • We then calculate (p-1)! % p using a for loop that runs from 1 to p - 1.
   • Inside the loop, we update factorialModP by multiplying it with i and taking the modulus p.
   • After the loop, we check if factorialModP is congruent to -1 modulo p, which indicates that p is prime according to Wilson's Theorem.
2. In the main() function, we declare an integer variable number and store user-provided value in it.
3. After that, we check if the input number is prime by calling the isPrimeWilson() function inside an if-else statement, passing the number variable as an argument.
4. If the function returns a non-zero value, we print that the number is prime.
5. If the function returns 0, we print that the number is not prime.
6. In this example, we use the input value 79, and the function returns a non-zero value, printing that the number is prime.

Time Complexity: O(n) 
Space Complexity: O(1) 

Prime Number Program In C Using Optimization By Skipping Even Iteration

This approach to writing a prime number program in C efficiently determines whether a given number is prime using an optimized approach that skips even iterations. Here is how this works-

• We first handle special cases, returning false for numbers less than or equal to 1 and true for 2, the only even prime number.
• For even numbers other than 2, it immediately returns false to skip unnecessary checks.
• Then, it iterates through odd numbers from 3 to the square root of the input number, checking for divisibility.
• If a divisor is found, the program returns false, indicating the number is not prime. Otherwise, it returns true, indicating the number is prime.

The sample C program given below provides the implementation of this approach to check for prime number.

Code Example:

I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRib29sLmg+CgovLyBGdW5jdGlvbiB0byBjaGVjayBpZiBhIG51bWJlciBpcyBwcmltZSAob3B0aW1pemVkIGJ5IHNraXBwaW5nIGV2ZW4gaXRlcmF0aW9uKQpib29sIGlzUHJpbWVPcHRpbWl6ZWQoaW50IG4pIHsKaWYgKG4gPD0gMSkgewpyZXR1cm4gZmFsc2U7fQoKaWYgKG4gPT0gMikgewpyZXR1cm4gdHJ1ZTt9CgppZiAobiAlIDIgPT0gMCkgewpyZXR1cm4gZmFsc2U7IC8vIFNraXAgZXZlbiBudW1iZXJzCn0KCmZvciAoaW50IGkgPSAzOyBpICogaSA8PSBuOyBpICs9IDIpIHsKaWYgKG4gJSBpID09IDApIHsKcmV0dXJuIGZhbHNlO30KfQpyZXR1cm4gdHJ1ZTsKfQoKaW50IG1haW4oKSB7CmludCBudW1iZXI7CnByaW50ZigiRW50ZXIgYSBudW1iZXIgdG8gY2hlY2sgaWYgaXQgaXMgcHJpbWU6ICIpOwpzY2FuZigiJWQiLCAmbnVtYmVyKTsKCi8vIENoZWNrIGFuZCBkaXNwbGF5IGlmIHRoZSBudW1iZXIgaXMgcHJpbWUKaWYgKGlzUHJpbWVPcHRpbWl6ZWQobnVtYmVyKSkgewpwcmludGYoIiVkIGlzIGEgcHJpbWUgbnVtYmVyLlxuIiwgbnVtYmVyKTsKfSBlbHNlIHsKcHJpbnRmKCIlZCBpcyBub3QgYSBwcmltZSBudW1iZXIuXG4iLCBudW1iZXIpOwp9CgpyZXR1cm4gMDsKfQ==

Output:

Enter a number to check if it is prime: 23
23 is a prime number.

Explanation:

In the C code- 

1. We define a function called isPrimeOptimized(), which takes an integer n as input and returns a boolean value indicating whether n is prime or not.
2. This function uses an optimization to skip even numbers in the loop. Inside the function-
   
   • We first check if n is less than or equal to 1. If it is, the function returns false, indicating that numbers less than or equal to 1 are not prime.
   • In case the first base check is not met, we check if n is equal to 2. If it is, the function returns true since 2 is a prime number.
   • If not, then we check if n is divisible by 2. If this is true, then the function returns false, indicating that n is not prime since all even numbers greater than 2 are not prime.
   • If none of the base checks are met, the program control moves into a for loop, which begins from 3 (skipping even numbers) up to the square root of n.
   • We increment the value of loop variable i by 2 in each iteration, effectively skipping even numbers.
   • In every loop iteration, we check if n is divisible by i. If it is, we return false, indicating that n is not prime.
   • If the loop completes without finding any divisor that evenly divides n, we return true, indicating that n is prime.
3. In the main() function, we declare an integer variable number and store the input value by the user in it with the printf() and scanf() functions.
4. We then check if the input number is prime by calling the isPrimeOptimized() function by passing the input number as an argument.
5. If the function returns true, the if-block prints that the number is prime.
6. If the function returns false, the else-block prints that the number is not prime.
7. In our example, we use input value 23, which is shown as a prime number.

Time Complexity: O(sqrt(n)/2) = O(sqrt(n))
Space Complexity: O(1)

Write Prime Number Program In C Using n/2 Iterations Optimization Approach

This approach efficiently checks whether a given number is prime using a user-defined function called isPrimeOptimizedByNOver2. Within the function, we iterate through potential divisors from 2 up to half of the input number (n/2).

• If the input number is less than or equal to 1, the function returns false.
• Otherwise, it checks if the input number is divisible by any of the potential divisors.
• If a divisor is found, the function returns false, confirming that the number is not prime.
• If no divisor is found within the specified range, the function returns true, indicating that the number is prime. 

Code Example:

I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRib29sLmg+CgovLyBGdW5jdGlvbiB0byBjaGVjayBpZiBhIG51bWJlciBpcyBwcmltZSAob3B0aW1pemVkIGJ5IG4vMiBpdGVyYXRpb25zKQpib29sIGlzUHJpbWVPcHRpbWl6ZWRCeU5PdmVyMihpbnQgbikgewppZiAobiA8PSAxKSB7CnJldHVybiBmYWxzZTt9Cgpmb3IgKGludCBpID0gMjsgaSA8PSBuIC8gMjsgKytpKSB7CmlmIChuICUgaSA9PSAwKSB7CnJldHVybiBmYWxzZTt9Cn0KcmV0dXJuIHRydWU7Cn0KCmludCBtYWluKCkgewppbnQgbnVtYmVyOwpwcmludGYoIkVudGVyIGEgbnVtYmVyIHRvIGNoZWNrIGlmIGl0J3MgcHJpbWU6ICIpOwpzY2FuZigiJWQiLCAmbnVtYmVyKTsKCi8vIENoZWNrIGFuZCBkaXNwbGF5IGlmIHRoZSBudW1iZXIgaXMgcHJpbWUKaWYgKGlzUHJpbWVPcHRpbWl6ZWRCeU5PdmVyMihudW1iZXIpKSB7CnByaW50ZigiJWQgaXMgYSBwcmltZSBudW1iZXIuXG4iLCBudW1iZXIpOwp9IGVsc2UgewpwcmludGYoIiVkIGlzIG5vdCBhIHByaW1lIG51bWJlci5cbiIsIG51bWJlcik7Cn0KCnJldHVybiAwOwp9

Output:

Enter a number to check if it's prime: 23
23 is a prime number.

Explanation:

In the code example-

1. We define a function called isPrimeOptimizedByNOver2(), which takes an integer n as input and returns a boolean value indicating whether n is prime or not.
2. This function uses an optimization to iterate only up to n / 2 for checking divisibility. Inside it-
   
   • Using an if-statement, we first check if n is less than or equal to 1. If it is, the function returns false, indicating that numbers less than or equal to 1 are not prime.
   • If the condition is not met, we move to a for loop to iterate through a range starting from 2 (i.e., loop initiation i=2) up to n / 2 (i.e., loop condition i<= n/2).
   • The loop condition i<=n/2 is how we skip n/2 iterations and optimize the approach to writing prime number program in C.
   • Inside the loop, we check if n is divisible by the loop variable i, using an if-statement. If it is, we return false, indicating that n is not prime.
   • If the loop completes without finding any divisor that evenly divides n, we return true, indicating that n is prime.
3. In the main() function, we declare an integer variable number and prompt the user to provide a value that we store in the variable.
4. Next, we check if the inputted value is a prime number by calling the isPrimeOptimizedByNOver2() function inside an if-else statement, with the number variable as its argument.
5. If the function returns true, the if-else statement prints that the number is prime.
6. If the function returns false, the if-else statement prints that the number is not prime.

Time Complexity: O(n/2)
Space Complexity: O(1)

Check & Print Prime Number In C Using While Loop

In this approach to find prime number in C we use a while loop inside a function to iterate through a range looking for potential divisors. The loop starts from 2 and goes up to the square root of the respective number. We check a few other chases like the number, say num, less than or equal to 1, or if it's divisible by any of the potential divisors. In such cases, the function returns false, indicating that the number is not prime. Otherwise, it returns true, confirming the number as prime. 

Below is a prime number program in C language that shows how we can use a while loop to check for prime numbers.

Code Example:

I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRib29sLmg+CiNpbmNsdWRlIDxtYXRoLmg+CgovLyBGdW5jdGlvbiB0byBjaGVjayBpZiBhIG51bWJlciBpcyBwcmltZSB1c2luZyB3aGlsZSBsb29wCmJvb2wgaXNQcmltZVdoaWxlTG9vcChpbnQgbikgewppZiAobiA8PSAxKSB7CnJldHVybiBmYWxzZTt9CgppbnQgZGl2aXNvciA9IDI7CndoaWxlIChkaXZpc29yIDw9IHNxcnQobikpIHsKaWYgKG4gJSBkaXZpc29yID09IDApIHsKcmV0dXJuIGZhbHNlO30KKytkaXZpc29yOwp9CnJldHVybiB0cnVlOwp9CgppbnQgbWFpbigpIHsKaW50IG51bWJlcjsKcHJpbnRmKCJFbnRlciBhIG51bWJlciB0byBjaGVjayBpZiBpdCBpcyBwcmltZTogIik7CnNjYW5mKCIlZCIsICZudW1iZXIpOwoKLy8gQ2hlY2sgYW5kIGRpc3BsYXkgaWYgdGhlIG51bWJlciBpcyBwcmltZQppZiAoaXNQcmltZVdoaWxlTG9vcChudW1iZXIpKSB7CnByaW50ZigiJWQgaXMgYSBwcmltZSBudW1iZXIuXG4iLCBudW1iZXIpOwp9IGVsc2UgewpwcmludGYoIiVkIGlzIG5vdCBhIHByaW1lIG51bWJlci5cbiIsIG51bWJlcik7Cn0KCnJldHVybiAwOwp9

Output:

Enter a number to check if it is prime: 31
31 is a prime number.

Explanation:

In the C code- 

1. We define a function called isPrimeWhileLoop(), which takes an integer n as input and returns a boolean value indicating whether n is prime or not. In the function-
   • Using an if-statement, we first check if n is less than or equal to 1. If this is true, the function returns false since the numbers less than or equal to 1 are not prime numbers.
   • Next, we initialize am integer type variable called divisor to the value of 2.
   • We then enter a while loop that continues as long as the loop condition is not satisfied- divisor is less than or equal to the square root of n, i.e., divisor <=sqrt(n).
   • Inside the loop, we use an if-statement to check if n is divisible by the value of the loop variable divisor with no remainder, i.e., n % divisor == 0.
   • If the condition is true, the function returns false, indicating that n is not prime.
   • If the loop completes all iterations without finding any divisor that evenly divides n, the function returns true, indicating that n is prime.
2. In the main() function, we declare an integer variable number to prompt the user to provide a value for it.
3. After that, we call the isPrimeWhileLoop() function by passing the number variable as an argument to check if the input number is prime.
4. If the function returns true, the printf() statement in the if-block displays the string message indicating that the number is prime.
5. If the function returns false, the printf() statement in the else-block displays the string message indicating that the number is not prime.
6. In this example, we test the input value 31, which is shown to be a prime number in the output console.

Time Complexity: O(sqrt(n))
Space Complexity: O(1)

Prime Number Program In C Using Functions

In this approach, we employ a user-defined function to find a prime number in C program. We can use any of the above-mentioned techniques to write the function. The unique benefit of a user-defined function is that it gives you the ability to pick which approach to follow and then use it for a variety of input without having to write new code. The example program in C below shows how to implement this.

Code Example:

I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRib29sLmg+CiNpbmNsdWRlIDxtYXRoLmg+CgovLyBGdW5jdGlvbiB0byBjaGVjayBpZiBhIG51bWJlciBpcyBwcmltZQpib29sIGlzUHJpbWUoaW50IG4pIHsKaWYgKG4gPD0gMSkKcmV0dXJuIGZhbHNlOwoKZm9yIChpbnQgaSA9IDI7IGkgKiBpIDw9IG47IGkrKykgewppZiAobiAlIGkgPT0gMCkKcmV0dXJuIGZhbHNlO30KcmV0dXJuIHRydWU7Cn0KCmludCBtYWluKCkgewppbnQgbnVtYmVyOwpwcmludGYoIkVudGVyIGEgbnVtYmVyOiAiKTsKc2NhbmYoIiVkIiwgJm51bWJlcik7CgovLyBDaGVjayBpZiB0aGUgbnVtYmVyIGlzIHByaW1lIHVzaW5nIHRoZSBpc1ByaW1lIGZ1bmN0aW9uCmlmIChpc1ByaW1lKG51bWJlcikpCnByaW50ZigiJWQgaXMgYSBwcmltZSBudW1iZXIuXG4iLCBudW1iZXIpOwplbHNlCnByaW50ZigiJWQgaXMgbm90IGEgcHJpbWUgbnVtYmVyLlxuIiwgbnVtYmVyKTsKCnJldHVybiAwOwp9

Output:

Enter a number: 17
17 is a prime number.

Explanation:

In the code- 

1. We define a function called isPrime(), which takes an integer n as input and returns a boolean value indicating whether n is prime or not.
   
   • In the function, we first check if n is less than or equal to 1. If it is, the function returns false, indicating that numbers less than or equal to 1 are not prime.
   • Next, the function contains a for loop that iterates through a range of number from 2 to the square root of n, looking for potential divisors.
   • For each value of loop variable i, if n is divisible by i with no remainder, the function returns false, indicating that n is not prime.
   • If none of the divisors divide n evenly, the function returns true, indicating that n is prime.
2. In the main() function, we declare an integer variable number and ask the user to provide a value for it, using the printf() and scanf() functions.
3. Next, we call the isPrime() number with the input number as an argument to check if the input number is prime. The function call is a part of an if-else statement.
4. If the function returns true, then the statement prints a message indicating that the number is prime.
5. Else, the function returns false and the statement prints a message indicating that the number is not prime.

Time Complexity: O(sqrt(n))
Space Complexity: O(1)

Prime Number Program In C Using Recursion

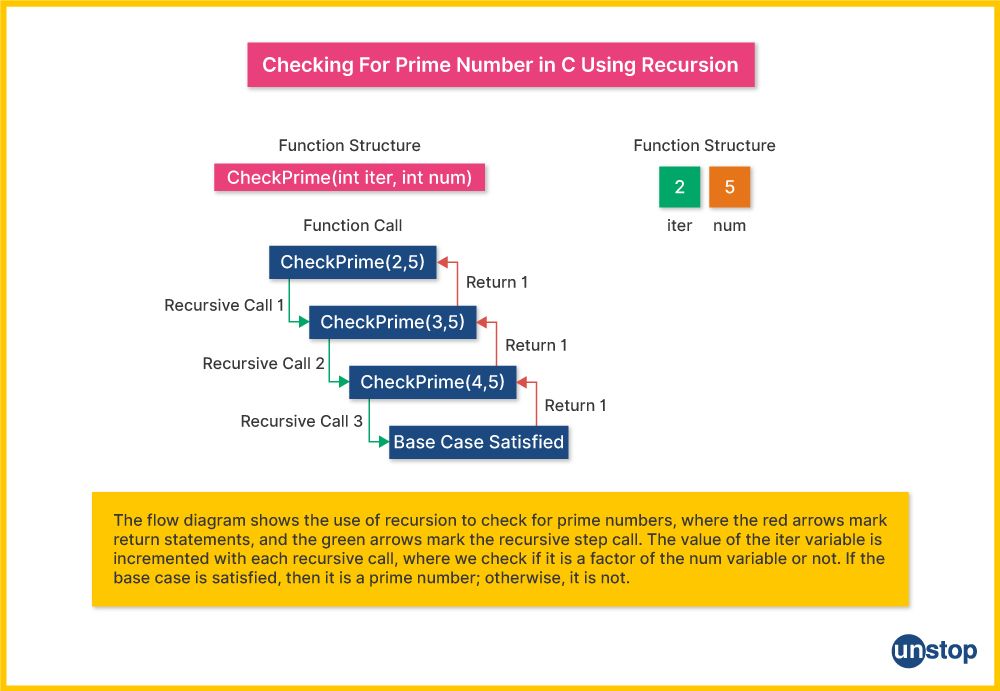
In this simple C program, we utilize a recursive approach to determine whether a given number is prime. Upon receiving user input, the program initiates a recursive function called isPrimeRecursive. This function iterates through potential divisors, starting from 2, up to the square root of the input number. At each step, it checks if the input number is divisible by the current divisor. If a divisor is found, indicating the number is not prime, the function returns false. Otherwise, if no divisor is found up to the square root, the function returns true, confirming the number as prime.

Code Example:

I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRib29sLmg+CiNpbmNsdWRlIDxtYXRoLmg+CgovLyBSZWN1cnNpdmUgZnVuY3Rpb24gdG8gY2hlY2sgaWYgYSBudW1iZXIgaXMgcHJpbWUKYm9vbCBpc1ByaW1lUmVjdXJzaXZlKGludCBuLCBpbnQgZGl2aXNvcikgewppZiAoZGl2aXNvciA+IHNxcnQobikpIHsgLy8gQmFzZSBjYXNlCnJldHVybiB0cnVlO30KCmlmIChuICUgZGl2aXNvciA9PSAwKSB7IC8vIE5vdCBwcmltZQpyZXR1cm4gZmFsc2U7fQoKLy8gUmVjdXJzaXZlbHkgY2FsbCB0aGUgZnVuY3Rpb24gd2l0aCB0aGUgbmV4dCBkaXZpc29yCnJldHVybiBpc1ByaW1lUmVjdXJzaXZlKG4sIGRpdmlzb3IgKyAxKTsKfQoKaW50IG1haW4oKSB7CmludCBudW07CnByaW50ZigiRW50ZXIgYSBudW1iZXIgdG8gY2hlY2sgaWYgaXQgaXMgcHJpbWU6ICIpOwpzY2FuZigiJWQiLCAmbnVtKTsKCi8vIENhbGxpbmcgcmVjdXJzaXZlIGZ1bmN0aW9uIGluc2lkZSBpZi1lbHNlIHN0YXRlbWVudCB0byBjaGVjayBmcm9tIHByaW1lIG51bWJlcgppZiAoaXNQcmltZVJlY3Vyc2l2ZShudW0sIDIpKSB7CnByaW50ZigiJWQgaXMgYSBwcmltZSBudW1iZXIuXG4iLCBudW0pOwp9IGVsc2UgewpwcmludGYoIiVkIGlzIG5vdCBhIHByaW1lIG51bWJlci5cbiIsIG51bSk7Cn0KCnJldHVybiAwOwp9

Output:

Enter a number to check if it is prime: 34
34 is not a prime number.

Explanation:

In the code- 

1. We define a recursive function called isPrimeRecursive(), which takes two integers n and divisor as parameters and returns a boolean value.
2. Inside the function, we use an if-statement to check if the divisor is greater than the square root of n, i.e., divisor > sqrt(n). If the condition is met, the function returns true, indicating that n is prime (base case of the recursion).
3. Next, the program checks if n is divisible by the divisor, i.e., n % divisor == 0. If the expression is true, the function returns false, indicating that n is not prime.
4. If neither of the previous cases is met, we recursively call the isPrimeRecursive() function with the next divisor (divisor + 1).
5. In the main() function, we declare an integer variable num and initialize it with the user provided input.
6. Next, we call the isPrimeRecursive() function inside an if-else statement.
7. The function takes the num variable and initial divisor value of 2 as inputs and checks if the user-provided input is prime.
8. If the function returns true, the if-block executes the printf() statement, indicating that the number is prime.
9. If the function returns false, the else-block executes the printf() statement, indicating that the number is not prime.

Time Complexity: O(sqrt(n))
Space Complexity: O(sqrt(n))

Prime Number Program In C Using For Loop

The for loop is a control construct/ control statement that helps iterate through an element/ structure and provides results depending on the conditions. We can use the for loop to iterate through a range of possible divisors for a given number to check if the respective number is prime or not. The naive approach to writing a prime number program in C discussed in the first section uses the for loop.

• We iterate over each number in the given range and check if it is prime using a for loop and a helper function isPrime.
• The isPrime function first checks whether a number is divisible by any number from 2 to itself - 1.
• If it's not divisible by any number, it returns true, indicating the number is prime. Otherwise, it returns false.

The pseudocode to describe the prime number logic in C program where we use for loop is given below.

Pseudocode: 

Function isPrime(num):
if num <= 1:
return false
for i from 2 to num - 1:
if num is divisible by i:
return false
return true

Main Function:
Input start and end numbers
For each number from start to end:
Check if it's prime using isPrime function
If prime, print it

Prime Number Program In C Using Sieve Of Eratosthenes

The Sieve of Eratosthenes is an algorithm used to find all prime numbers up to a specified integer n. It works by iteratively marking the multiples of each prime number starting from 2 as composite (not prime). Here's how you can write a prime number program in C using this approach:

1. Create a boolean array prime[0..n] and initialize all entries to true. Initially, all numbers are assumed to be prime.
2. Starting from 2, mark all multiples of 2 as not prime.
3. Find the next number not marked as composite (prime[i] is true) and mark all its multiples as not prime.
4. Repeat step 3 until p*p is greater than n.
5. All remaining numbers marked as prime are prime numbers.

The algorithm eliminates the need for division in the prime checking process, which makes it more efficient than the naive approach of checking divisibility by all numbers up to the square root of n.

Pseudocode for Prime Number Program in C Using the Sieve of Eratosthenes:

function SieveOfEratosthenes(n)
Let prime[0..n] be a boolean array initialized to true

prime[0] = prime[1] = false // 0 and 1 are not prime

for p from 2 to sqrt(n) do
if prime[p] is true then
for i from p*p to n with step p do
prime[i] = false

Output all prime numbers p where prime[p] is true

The pseudocode above describes the prime number logic in C program to find prime numbers. The code example below provides a complete implementation of this approach.

Code Example:

I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRib29sLmg+CiNpbmNsdWRlIDxtYXRoLmg+Cgp2b2lkIHNpZXZlT2ZFcmF0b3N0aGVuZXMoaW50IG4pIHsKYm9vbCBwcmltZVtuICsgMV07CmZvciAoaW50IGkgPSAwOyBpIDw9IG47IGkrKykKcHJpbWVbaV0gPSB0cnVlOwoKcHJpbWVbMF0gPSBwcmltZVsxXSA9IGZhbHNlOwoKZm9yIChpbnQgcCA9IDI7IHAgKiBwIDw9IG47IHArKykgewppZiAocHJpbWVbcF0gPT0gdHJ1ZSkgewpmb3IgKGludCBpID0gcCAqIHA7IGkgPD0gbjsgaSArPSBwKQpwcmltZVtpXSA9IGZhbHNlOwp9Cn0KCnByaW50ZigiUHJpbWUgbnVtYmVycyB1cCB0byAlZCBhcmU6ICIsIG4pOwpmb3IgKGludCBwID0gMjsgcCA8PSBuOyBwKyspCmlmIChwcmltZVtwXSkKcHJpbnRmKCIlZCAiLCBwKTsKfQoKaW50IG1haW4oKSB7CmludCBuOwpwcmludGYoIkVudGVyIGEgbnVtYmVyOiAiKTsKc2NhbmYoIiVkIiwgJm4pOwpzaWV2ZU9mRXJhdG9zdGhlbmVzKG4pOwpyZXR1cm4gMDsKfQ==

Output:

Enter a number: 43
Prime numbers up to 43 are: 2 3 5 7 11 13 17 19 23 29 31 37 41 43

Explanation:

In this example- 

1. We begin by defining a function called sieveOfEratosthenes(), which takes an integer n as input.
2. Inside the function, we declare a boolean array called prime of size n + 1 to mark numbers as prime or non-prime.
3. Next, we use a for loop to initialize all elements of the prime array to true, assuming initially that all numbers are prime.
4. We explicitly mark 0 and 1 as non-prime by setting prime[0] and prime[1] to false.
5. After that, we use another for loop to iterate through numbers starting from 2 up to the square root of n.
6. For each prime number p, if prime[p] is true, indicating that p is prime, we mark all multiples of p as non-prime.
7. We start marking multiples of p from p * p, as smaller multiples of p would have already been marked by smaller prime numbers.
8. After marking all non-prime numbers, we print the message "Prime numbers up to n are: ".
9. We then iterate through the prime array and print the numbers that are still marked as prime.
10. In the main() function, we declare an integer variable n to store the user input.
11. We then prompt the user to provide a value for n and store it in the variable using printf(), scanf(), and the reference/ address-of operator (&).
12. Finally, we call the sieveOfEratosthenes() function with the input number to print prime numbers up to that limit.
13. The program returns 0 to indicate successful execution.

Time Complexity: O(n * log(log(n)))
Space Complexity: O(n)

C Program To Find Prime Number In A Range (Or Between Two Integers)

There is a possibility that you might need to check for prime numbers within a range rather than checking if a specific number is prime. We can follow the same approach of writing a prime number program in C by defining a function that iterates from 2 to the square root of the number.

• If the number is less than or equal to 1, it's not prime.
• Within the loop, if the number is divisible by any i, it's not prime, and the function returns 0.
• If no divisors are found, the function returns 1, indicating the number is prime.
• In the main function, the program prompts the user to input a range of numbers and iterates through each number.
• It calls the isPrime function to check for primality, and if a number is prime, it's printed.

This approach minimizes unnecessary checks by iterating only up to the square root of each number, optimizing performance for prime number identification within the specified range.

Code Example:

I2luY2x1ZGUgPHN0ZGlvLmg+CgppbnQgaXNQcmltZShpbnQgbnVtKSB7CmlmIChudW0gPD0gMSkgcmV0dXJuIDA7IC8vIE51bWJlcnMgbGVzcyB0aGFuIG9yIGVxdWFsIHRvIDEgYXJlIG5vdCBwcmltZQpmb3IgKGludCBpID0gMjsgaSAqIGkgPD0gbnVtOyBpKyspIHsKaWYgKG51bSAlIGkgPT0gMCkgcmV0dXJuIDA7IC8vIElmIG51bSBpcyBkaXZpc2libGUgYnkgYW55IGksIGl0J3Mgbm90IHByaW1lCn0KcmV0dXJuIDE7IC8vIElmIG5vIGRpdmlzb3JzIGZvdW5kLCBudW0gaXMgcHJpbWUKfQoKaW50IG1haW4oKSB7CmludCBzdGFydCwgZW5kOwpwcmludGYoIkVudGVyIHR3byBudW1iZXJzOiAiKTsKc2NhbmYoIiVkICVkIiwgJnN0YXJ0LCAmZW5kKTsKcHJpbnRmKCJQcmltZSBudW1iZXJzIGJldHdlZW4gJWQgYW5kICVkIGFyZTogIiwgc3RhcnQsIGVuZCk7CmZvciAoaW50IGkgPSBzdGFydDsgaSA8PSBlbmQ7IGkrKykgewppZiAoaXNQcmltZShpKSkgcHJpbnRmKCIlZCAiLCBpKTsgLy8gSWYgaSBpcyBwcmltZSwgcHJpbnQgaXQKfQpyZXR1cm4gMDsKfQ==

Output:

Enter two numbers: 5 10
Prime numbers between 5 and 10 are: 5 7

Explanation:

In the above block of code-

1. We define a function isPrime() that takes an integer num as input and returns 1 if num is prime; otherwise, it returns 0.
2. In the function, we first check if num is less than or equal to 1 using an if-statement. If so, the function returns 0, indicating that numbers less than or equal to 1 are not prime.
3. Next, we use a for loop starting from 2 to the square root of num to iterate through a range and check for prime numbers.
   
   • Inside the loop, we check if num is divisible by the loop variable i. If it is, then num is not prime, so we return 0.
   • If no divisors are found within the loop, we return 1, indicating that num is prime.
4. In the main() function, we declare two integers, start and end.
5. We then prompt the user to enter two numbers and read the input numbers using scanf().
6. After that, we use a printf() statement to display the message- "Prime numbers between start and end are: " to the console.
7. Then, we employ a for loop to iterate the range of numbers from the value of start to end.
8. In the loop, we check if each number is prime using the isPrime() function.
9. If the function returns 1 for a specific number, then that is a prime number which is then printed to the console.
10. As shown in the output window, the two prime numbers within input range, 5 and 10, are 5 and 7.

Time Complexity: O((end - start) * sqrt(n))
Space Complexity: O(1) 

Comparison of Complexities

We can determine if a method to write a prime number program in C is more efficient in comparison to another by analysing the time complexities of different approaches. The table given below provides this comparison with the methods ordered from least to most efficient based on their time complexity.

A lower time complexity indicates a more efficient algorithm. Note that the actual performance may vary based on specific use cases and input sizes.

Conclusion

In this comprehensive exploration of various approaches to writing a prime number program in C, we have discussed everything, starting from naive methods to optimized strategies. Each type of method offers a unique balance of simplicity and efficiency, catering to different use cases and input sizes. While the naive approach serves as a foundation, more sophisticated methods like utilizing the square root of the input number, Wilson's theorem, and optimizations by skipping even iterations and reducing iterations by half significantly enhance the performance of C programs.

We have provided a thorough understanding of each technique to find prime numbers in C program with the help of pseudocode, code examples, explanations, and complexity analysis. As we compare the complexities, it becomes evident that optimized methods, such as the Sieve of Eratosthenes, offer the most efficient solution for finding prime numbers within large ranges. However, the choice of algorithm depends on the specific requirements of the application, considering factors like input size, computational resources, and time constraints.

Also Read: 100+ Top C Interview Questions With Answers (2024)

Frequently Asked Questions

Q. What are prime numbers, and why are they important?

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In other words, a prime number is divisible only by 1 and itself, without leaving a remainder.

Prime numbers are important for several reasons:

1. Cryptography: Prime numbers play a crucial role in modern cryptography, particularly in encryption algorithms such as RSA. The security of these algorithms relies on the difficulty of factoring large composite numbers into their prime factors.
2. Number Theory: Prime numbers are fundamental objects in number theory, which is the study of the properties and relationships of numbers. Many important theorems and conjectures in mathematics are related to prime numbers, such as the Goldbach conjecture and the twin prime conjecture.
3. Computer Science: Prime numbers have applications in various areas of computer science. They are used in hashing algorithms, generating random numbers, optimizing algorithms, and checking for unique identifiers.
4. Data Structures: Prime numbers are used in data structures such as hash tables to distribute data evenly across the available slots, reducing the likelihood of collisions and improving efficiency.
5. Coding and Puzzles: Prime numbers often appear in coding challenges, puzzles, and recreational mathematics problems. They serve as the basis for creating interesting and challenging problems that stimulate logical and analytical thinking.

Q. How can one determine the factors of prime numbers?

The factors of a prime number are limited to the number itself and 1. A prime number is defined as a natural number greater than 1 that is not a product of two smaller natural numbers. There are no other factors since it has only two distinct positive divisors (1 and itself).

For example:
Factors of 2: 1, 2
Factors of 3: 1, 3
Factors of 5: 1, 5
Factors of 17: 1, 17

In general, when you have a prime number, the only positive divisors it has are 1 and the number itself. 

Q. Why is the number 1 not considered a prime number?

The number 1 is not considered a prime number because it fails to meet the definition of a prime number. By definition, a prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.

However, 1 does not meet this criterion, as it only has one positive divisor, which is 1 itself. It lacks a second distinct positive divisor, making it an exception to the definition of prime numbers. Including 1 in the set of prime numbers would contradict the fundamental properties and definitions of prime numbers, leading to inconsistencies in mathematical theory and calculations. Therefore, to maintain the integrity of prime number theory, 1 is excluded from the set of prime numbers.

Q. How can twin prime numbers be identified in C?

Twin prime numbers are pairs of prime numbers that have a difference of 2. In C, you can identify twin prime numbers by iterating through each number in a given range and checking if both the number and its neighbour (i.e., number + 2 or number - 2) are prime. Here's a basic approach to writing a prime number program in C to find twins:

1. Write a function to check if a given number is prime.
2. Iterate through each number in the range and check if it is prime.
3. For each prime number found, check if its neighbour (number + 2 or number - 2) is also prime.
4. If both the number and its neighbour are prime, they form a twin prime pair.

Here's a simple example code in C to identify twin prime numbers within a specified range.

Code Example: 

I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRib29sLmg+CiNpbmNsdWRlIDxtYXRoLmg+CgovLyBGdW5jdGlvbiB0byBjaGVjayBpZiBhIG51bWJlciBpcyBwcmltZQpib29sIGlzUHJpbWUoaW50IG4pIHsKaWYgKG4gPD0gMSkKcmV0dXJuIGZhbHNlOwpmb3IgKGludCBpID0gMjsgaSA8PSBzcXJ0KG4pOyBpKyspIHsKaWYgKG4gJSBpID09IDApCnJldHVybiBmYWxzZTsKfQpyZXR1cm4gdHJ1ZTsKfQoKaW50IG1haW4oKSB7CmludCBzdGFydCwgZW5kOwpwcmludGYoIkVudGVyIHRoZSByYW5nZSB0byBmaW5kIHR3aW4gcHJpbWUgbnVtYmVyczogIik7CnNjYW5mKCIlZCAlZCIsICZzdGFydCwgJmVuZCk7CgpwcmludGYoIlR3aW4gcHJpbWUgbnVtYmVycyBiZXR3ZWVuICVkIGFuZCAlZCBhcmU6XG4iLCBzdGFydCwgZW5kKTsKZm9yIChpbnQgaSA9IHN0YXJ0OyBpIDw9IGVuZCAtIDI7IGkrKykgewppZiAoaXNQcmltZShpKSAmJiBpc1ByaW1lKGkgKyAyKSkgewpwcmludGYoIiglZCwgJWQpXG4iLCBpLCBpICsgMik7Cn0KfQpyZXR1cm4gMDsKfQ==

Output: 

Enter the range to find twin prime numbers: 7 15
Twin prime numbers between 7 and 15 are:
(11, 13)

Explanation: 

This code prompts the user to input a range and then iterates through each number in that range. For each number, it checks if both the number and its neighbour (number + 2) are prime. If they are, it prints the twin prime pair.

Q. What are the trade-offs between the naive approach and the Sieve of Eratosthenes?

The trade-offs between the naive approach and the Sieve of Eratosthenes to writing a prime number program in C lie primarily in their efficiency and simplicity.

The naive approach, while straightforward to implement, becomes increasingly inefficient as the range of numbers to check for primality grows. This inefficiency stems from its need to iterate through each number in the range and perform a division check for every number, resulting in a time complexity of O(n√n). Consequently, for large ranges, the naive approach can be impractical due to its slow execution speed.

In contrast, the Sieve of Eratosthenes offers significantly improved efficiency by eliminating unnecessary division operations. By iteratively marking the multiples of each prime number as composite, the Sieve drastically reduces the number of divisions needed to determine primality. This results in a time complexity of O(n log log n), making it much faster than the naive approach to writing a prime number program in C, especially for large input range values.

Check out the following to expand your knowledge of C programming topics:

1. Operators In C Programming: Explained With Examples
2. The Sizeof() Operator In C | A Detailed Explanation (+Examples)
3. Pointers In C | Ultimate Guide With Easy Explanations (+Examples)
4. Compilation In C | Detail Explanation Using Diagrams & Examples
5. Bitwise Operators In C Programming Explained With Code Examples