- What Is Recursion In C?
- Basic Syntax Of Recursion In C
- Fundamentals Of Recursion In C
- How Does Recursion Work In C?
- Types Of Recursion In C
- Memory Allocation Of Recursive Method In C
- Properties Of Recursion In C
- Examples Of Recursion In C
- Advantages & Disadvantages Of Recursion In C
- Difference Between Iteration & Recursion In C
- Difference Between Direct & Indirect Recursion In C
- Conclusion
- Frequently Asked Questions
Recursion In C | Components, Working, Types & More (+Examples)
Recursion, a fascinating and powerful concept in computer programming, lies at the heart of many algorithmic solutions. It's a technique where a function calls itself, either directly or indirectly, to solve a problem. In this article, we will discuss everything about recursion in C programming language, its syntax, how it operates, and types of recursion with the help of examples. We'll explore the advantages and disadvantages of recursion, distinguish it from iteration, and address common questions about this programming technique.
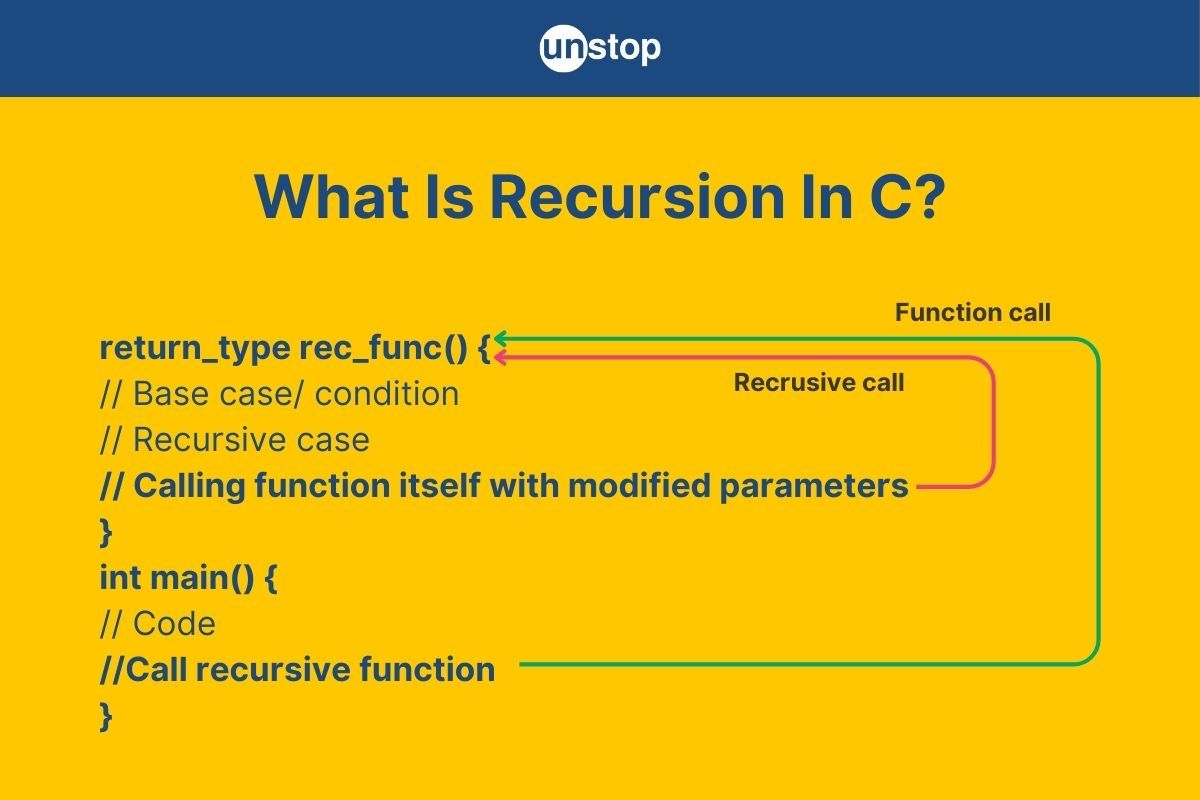
What Is Recursion In C?
Recursion in C programming involves a function calling itself to solve problems by breaking them down into smaller parts. Unlike using loops for tasks, recursion repeatedly applies a set of rules by including a function call within the function definition itself.
- In other words, recursion is based on the idea of self-reference.
- This technique efficiently solves challenging problems by simplifying them into subproblems.
- When a function uses recursion, it performs part of a task and delegates the remaining task to another instance.
The process of recursion/ recursive calls continues until it reaches a condition called the base case. The base case is essential as it prevents the function from calling itself and ensures that it terminates, resolving the problem.
Why Use Recursion In C Programming?
As we've mentioned, recursion lies at the heart of many programming algorithms. Here are the primary reasons why we need to use recursion in programming:
- Simplicity and Elegance: Recursion often leads to simpler and more elegant solutions for certain problems, especially those that can be naturally expressed in smaller instances of the same problem.
- Reduction of Complexity: Recursion in C can help reduce the complexity of code by breaking down a problem into smaller, manageable parts, making it easier to understand and maintain.
- Efficiency: In some cases, recursion can be more efficient than iterative approaches, particularly when dealing with tree-like structures or problems that can be naturally solved recursively.
- Natural Fit for Data Structures: Recursive functions are particularly well-suited for working with recursive data structures like trees and graphs. For instance, traversing a binary tree is more intuitive using recursion than iteration.
- Backtracking Solutions: Recursion is the go-to approach for solving backtracking problems such as the N-Queens puzzle, Sudoku solver, or generating permutations/combinations. It allows for clean branching and backtracking without complex state management.
- Cleaner State Management: Since each recursive call has its own stack frame, it eliminates the need for manual state tracking that might be required in loops, especially when exploring different paths or branches.
- Mathematical Problem Solving: Problems with inherent mathematical recurrence relations- like computing factorial, Fibonacci numbers, or GCD- can be directly translated into recursive C functions, making the code closely resemble the mathematical expression.
Real-Life Example Of Recursion In C
Imagine a large filing cabinet in an office, and the cabinet has multiple folders. Some of these folders might contain more folders in addition to documents. Your job is to find a folder that contains only documents and no folders.
This seemingly complex problem can be defined using recursion. Here, you would go through every folder and close it if there are only documents. If the folder has more folders, then you sort each one out just like the first one. In the recursive terms, this can be explained as
- Function Call (Opening a Folder): Opening a folder is like calling a function. You open it to see what's inside.
- Base Case (Folder with Only Documents): A folder that contains only documents and no further folders represents the base case in recursion. Once you reach this folder, you stop opening more folders.
- Recursive Step (Folders Inside Folders): When you find a folder inside another folder, you open it, continuing the process. This is like the recursive step in a function, where the function calls itself with a smaller or simpler problem.
In essence, recursion involves breaking down a problem into simpler, similar sub-problems, and the solution to the original problem is built up from the solutions to these sub-problems.
Basic Syntax Of Recursion In C
return_type function_name(parameters) {
if (condition) { // Base condition
// termination statement
}else { // Recursive case
// recursive call to the function
}
}
Here,
- The terms function_name and return_type refer to the recursive function name/ identifier and the data type of its return value, respectively.
- Parameters refer to the input variables that the function takes.
- The if keyword marks the if-else statement for defining base and recursive cases.
- The if-block has the base condition, which, if true, stops the recursive calls as stipulated by the block's termination statement/ return statement.
- Lastly, the else-block contains the recursive case/ recursive call, which defines how the function calls itself using modified parameters.
Look at the simple C program example below, where we generate the nth number of the Fibonacci series, to understand this concept better.
Code Example:
#include
// Recursive function to calculate the nth term in the Fibonacci sequence
int fibonacci(int n) {
// Base cases: if n is 0 or 1, return n
if (n == 0 || n == 1) {
return n;
}
// Recursive case: return fibonacci(n - 1) + fibonacci(n - 2)
else {
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
int main() {
int term = 6; // Example input to find the 6th term in the Fibonacci sequence
int result = fibonacci(term);
printf("The %dth term in the Fibonacci sequence is: %d\n", term, result);
return 0;
}
I2luY2x1ZGUgPHN0ZGlvLmg+CgovLyBSZWN1cnNpdmUgZnVuY3Rpb24gdG8gY2FsY3VsYXRlIHRoZSBudGggdGVybSBpbiB0aGUgRmlib25hY2NpIHNlcXVlbmNlCmludCBmaWJvbmFjY2koaW50IG4pIHsKLy8gQmFzZSBjYXNlczogaWYgbiBpcyAwIG9yIDEsIHJldHVybiBuCmlmIChuID09IDAgfHwgbiA9PSAxKSB7CnJldHVybiBuOwp9Ci8vIFJlY3Vyc2l2ZSBjYXNlOiByZXR1cm4gZmlib25hY2NpKG4gLSAxKSArIGZpYm9uYWNjaShuIC0gMikKZWxzZSB7CnJldHVybiBmaWJvbmFjY2kobiAtIDEpICsgZmlib25hY2NpKG4gLSAyKTsKfQp9CgppbnQgbWFpbigpIHsKaW50IHRlcm0gPSA2OyAvLyBFeGFtcGxlIGlucHV0IHRvIGZpbmQgdGhlIDZ0aCB0ZXJtIGluIHRoZSBGaWJvbmFjY2kgc2VxdWVuY2UKaW50IHJlc3VsdCA9IGZpYm9uYWNjaSh0ZXJtKTsKcHJpbnRmKCJUaGUgJWR0aCB0ZXJtIGluIHRoZSBGaWJvbmFjY2kgc2VxdWVuY2UgaXM6ICVkXG4iLCB0ZXJtLCByZXN1bHQpOwoKcmV0dXJuIDA7Cn0=
Output:
The 6th term in the Fibonacci sequence is: 8
Explanation:
In the simple C code example, we first include the standard input-output header file/ library for basic input and output operations.
- We define a recursive function called fibonacci(), which takes integer data type variable n as a parameter and calculates the nth term in the Fibonacci sequence.
- Inside the function, we use an if-else statement to define the base and recursive case.
- In the base cases, the if-condition checks if n is equal to 0 or 1, using the equality relational operator and logical OR operator.
- If the overall condition is true, then the function returns n itself, as the Fibonacci sequence starts with 0 and 1.
- If the condition, n==0 || n==1 is false, we move to the recursive case in the else block.
- In the recursive case, the function returns the sum of the previous two terms in the Fibonacci sequence, computed recursively using the expression fibonacci(n - 1) + fibonacci(n - 2).
- In the main() function, we declare an integer variable term and assign the value 6 to it.
- Then, we call the fibonacci() function, passing term as an argument and store the outcome in the variable result.
- The function calculates the 6th term of the Fibonacci sequence since value of term is 6.
- We then use the printf() function to print this value along with formatted string message. Here, the %d format specifier indicates an integer value, and the newline escape sequence (\n) shifts the cursor to the next line.
- Finally, the main() function terminates with a return 0 statement, indicating successful execution without any errors.
Fundamentals Of Recursion In C
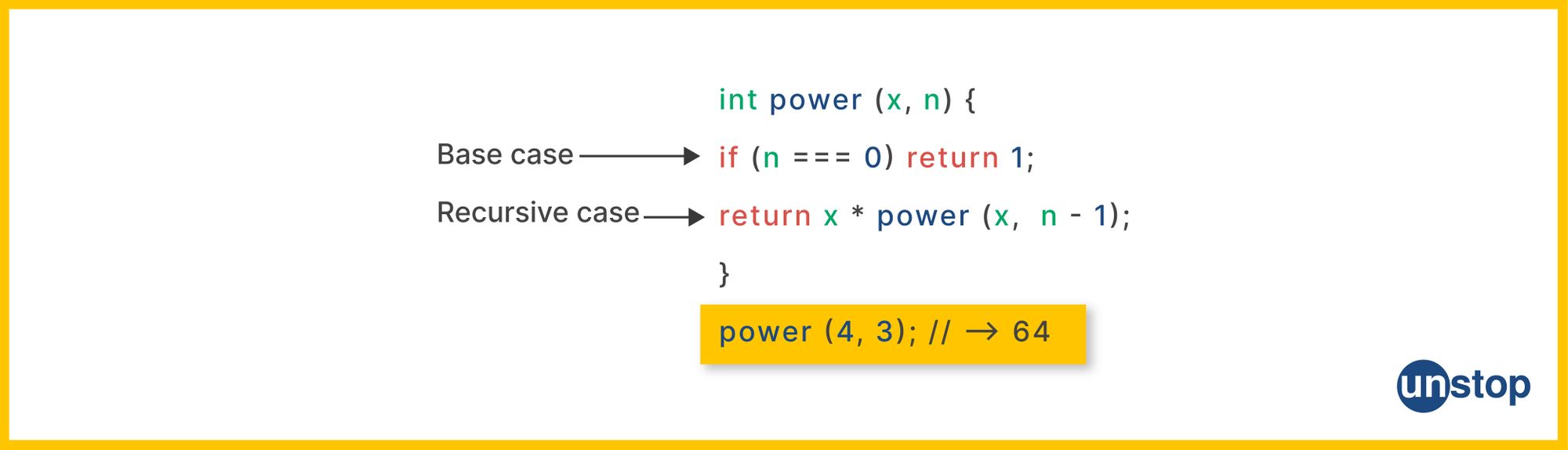
The recursion case and base case are two objects that make up the fundamentals of recursion and are necessary components of any recursive function. Let's understand them in detail:
Recursion Case In Recursion In C
The recursion case is the part of a recursive function where the function calls itself with modified parameters. Defining the recursive case is how we break down the bigger problem into smaller, more manageable subproblems.
This breakdown continues until the problem reaches a base case where the recursion stops. The recursive case typically follows a pattern where the function calls itself with parameters that bring it closer to the base case, eventually leading to the termination of recursion.
Example:
int factorial(int n) {
// Base case: if n is 0 or 1, return 1
if (n == 0 || n == 1) {
return 1;
}
// Recursive case: return n * factorial(n - 1)
else {
return n * factorial(n - 1); // Recursive call with modified parameter
}
}
In the C example program, the recursive case n * factorial(n - 1) calls the factorial function with the parameter n - 1, bringing the problem closer to the base case of n = 0 or n = 1.
Base Condition In Recursion In C
The base condition, also known as the base case or termination condition, is the condition that defines when the recursion should stop. It serves as the exit condition for the recursive function and prevents infinite recursion.
The base condition specifies a scenario where the function can directly return a result without making further recursive calls. It represents the smallest instance of the problem that can be solved without recursion.
Example:
int factorial(int n) {
// Base case: if n is 0 or 1, return 1
if (n == 0 || n == 1) { // Base condition
return 1; // Return 1 to terminate recursion
}
else {
return n * factorial(n - 1); // Recursive case
}
}
In the C example code, the base condition if (n == 0 || n == 1) checks if n is either 0 or 1. If the base condition is met, the function returns 1, terminating the recursion. Otherwise, the function proceeds to the recursive case.
What Is Recursive Function In C?
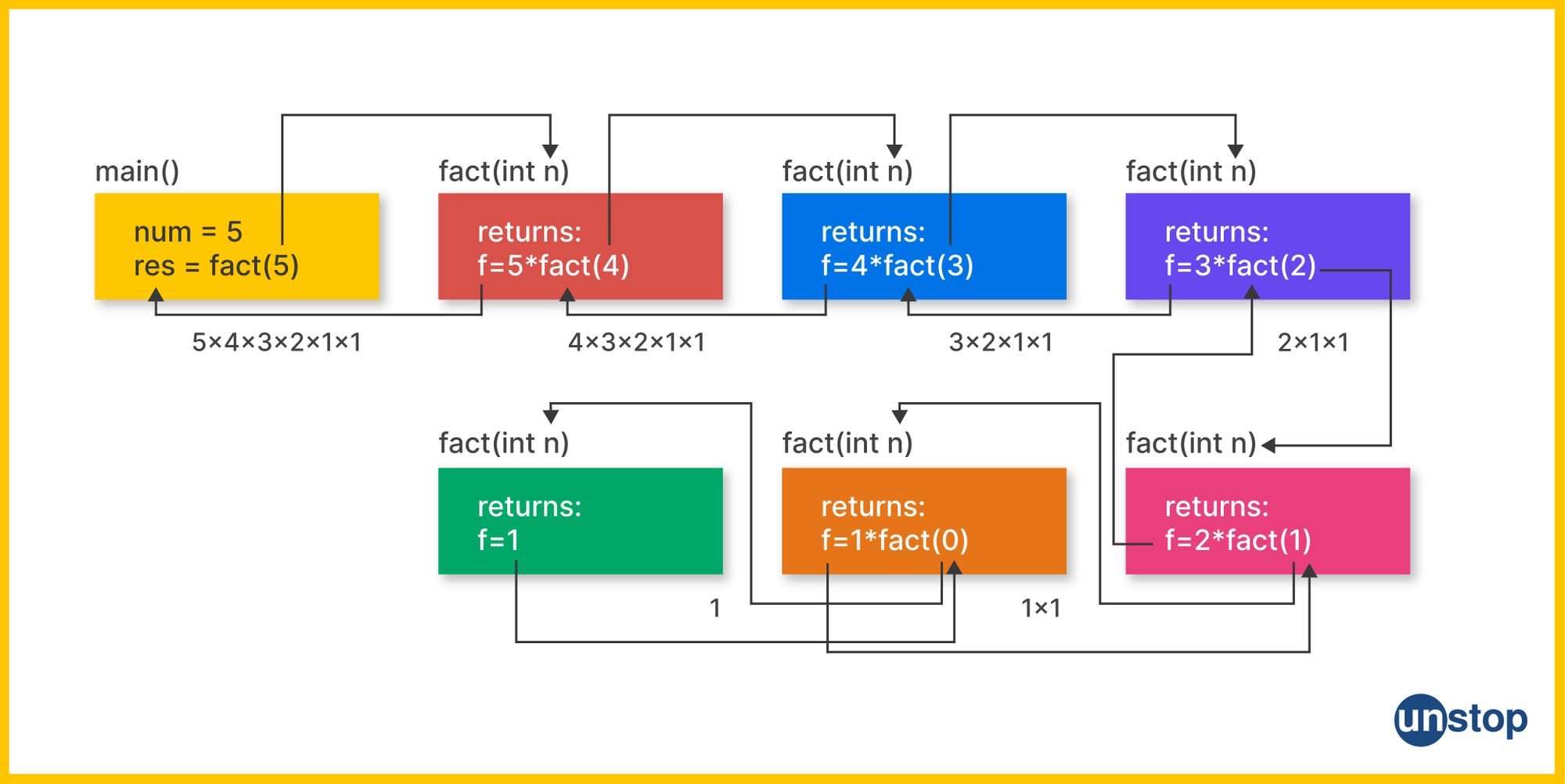
A function in programming is a self-contained block of code that performs a specific task. It takes input (parameters), performs some operations, and optionally returns a result. They help organize code, promote reusability, and improve readability in C programs.
A recursive function in C is a function that calls itself either directly or indirectly during its execution. This technique is particularly useful for solving problems that can be broken down into smaller subproblems of the same type. Recursive functions follow a specific structure:
- Base Case: Defines the termination condition for the recursion. It specifies when the function should stop calling itself and return a result.
- Recursive Case: Defines the logic for calling the function itself with modified parameters. It represents the part of the function where recursion occurs.
Pseudocode For Recursive Functions In C
// Recursive function to calculate the factorial of a number
int factorial(int n) {
// Base case: if n is 0 or 1, return 1
if (n == 0 || n == 1) {
return 1;
} else {
// Recursive case: return n * factorial(n - 1)
return n * factorial(n - 1);
}
}
Here,
-
Function Definition: The pseudocode begins with the definition of the factorial function, which takes an integer parameter n and returns an integer value.
- Base Case: The pseudocode checks for the base case, which occurs when n is either 0 or 1.
- If n is 0 or 1, the function returns 1 immediately without further recursion.
- Base cases are crucial in recursive functions to prevent infinite recursion and provide a termination condition.
- Recursive Case: If n is greater than 1 (i.e., not a base case), the pseudocode proceeds to the recursive case.
- In the recursive case, the function calls itself recursively with the argument n-1.
- This recursive call generates a sequence of function calls, each with a decreasing value of n, until the base case is reached.
-
Return Statement: After the recursive call, the pseudocode returns the result of the current function call multiplied by n. This multiplication operation effectively calculates the factorial of n by multiplying n with the factorial of n-1.
-
Termination: The recursive calls continue until the base case is reached. Once the base case is reached, the recursion stops, and the function returns the final result.
How Does Recursion Work In C?
Here is a step-by-step description of the recursion process/ working of a recursive function in C programs:
- Function Call: When a recursive function is called with a certain input, it enters the execution phase like any other function.
- Base Case Check: The function first checks if the current input satisfies the base case condition. If the base case is met, the function returns a specific value, terminating the recursion.
- Recursive Case & Recursive Calls: If the base case is not met, the function proceeds to the recursive case, where it calls itself with modified parameters. These recursive calls and modified parameters typically bring the problem closer to the base case, allowing the function to eventually reach it.
- Function Invocation Stack: Each time the function calls itself recursively, a new instance of the function is added to the call stack. This stack keeps track of all the function calls and their corresponding parameters and local variables.
- Return Value Propagation: As the recursion unwinds, return values from each recursive call are propagated back to the previous invocation. These return values may be combined or processed as necessary, contributing to the final result.
- Termination: Once the base case is reached, the recursion stops, and the function returns the final result. The call stack is then gradually unwound as each function call completes, releasing the memory allocated for each call.
Note: Recursion in C involves the allocation of memory on the call stack for each recursive call. It's essential to manage memory efficiently to avoid stack overflow errors, which occur when the call stack exceeds its memory limit.
Let's consider a sample C program that illustrates how to use recursion to countdown before launching a rocket.
Code Example:
#include
void countdown(int seconds) {
// Base case: countdown reaches zero
if (seconds == 0) {
printf("Blastoff!\n");
} else {
// Display the current second
printf("%d seconds\n", seconds);
// Recursive call with a smaller value
countdown(seconds - 1);
}
}
int main() {
int initialSeconds = 3;
countdown(initialSeconds);
return 0;
}
I2luY2x1ZGUgPHN0ZGlvLmg+Cgp2b2lkIGNvdW50ZG93bihpbnQgc2Vjb25kcykgewovLyBCYXNlIGNhc2U6IGNvdW50ZG93biByZWFjaGVzIHplcm8KaWYgKHNlY29uZHMgPT0gMCkgewpwcmludGYoIkJsYXN0b2ZmIVxuIik7Cn0gZWxzZSB7Ci8vIERpc3BsYXkgdGhlIGN1cnJlbnQgc2Vjb25kCnByaW50ZigiJWQgc2Vjb25kc1xuIiwgc2Vjb25kcyk7Ci8vIFJlY3Vyc2l2ZSBjYWxsIHdpdGggYSBzbWFsbGVyIHZhbHVlCmNvdW50ZG93bihzZWNvbmRzIC0gMSk7Cn0KfQoKaW50IG1haW4oKSB7CgppbnQgaW5pdGlhbFNlY29uZHMgPSAzOwpjb3VudGRvd24oaW5pdGlhbFNlY29uZHMpOwoKcmV0dXJuIDA7Cn0=
Output:
3 seconds
2 seconds
1 seconds
Blastoff!
Explanation:
In the sample C code-
- We define a recursive function countdown(), which takes an integer variable as input and simulates a countdown timer.
- Inside the function, we have an if-else statement wherein-
- The if-block, i.e., base case, checks if value of seconds is equal to 0. If this condition is true, then the function prints the string message- Blastoff!, indicating the end of the countdown.
- If the condition is false, we move to the recursive case in the else-block.
- In the recursive case, the function prints the current value of seconds and then re-calls itself with the modified value, i.e., (seconds - 1).
- This continues until the base case is satisfied and the function terminates.
- In the main() function, we initialize the variable initialSeconds with 5, representing the initial number of seconds for the countdown.
- Then, we call the countdown() function with initialSeconds as the argument to start the countdown.
- The function recursively decrements the value of the seconds variable until it reaches 0 and the base case is met.
- In every recursive call, the function prints the current value of second at each step and finally prints- Blastoff! to indicate the end of the countdown.
Types Of Recursion In C
Recursion in C can be categorized into two main types, i.e., direct Recursion and Indirect Recursion. Each type has its characteristics and use cases.
Direct Recursion In C
Direct recursion occurs when a function calls itself directly. In other words, the function makes a recursive call to itself within its own definition. This is the most common form of recursion and is often used to solve problems that can be broken down into smaller subproblems.
Syntax:
return_type recursiveFunction(parameters) {
// Base case check
if (base_condition) {
// Termination condition
return base_value;
}
// Recursive case
return recursiveFunction(modified_parameters);
}
This is the same syntax we discussed in the sections above.
Indirect Recursion In C
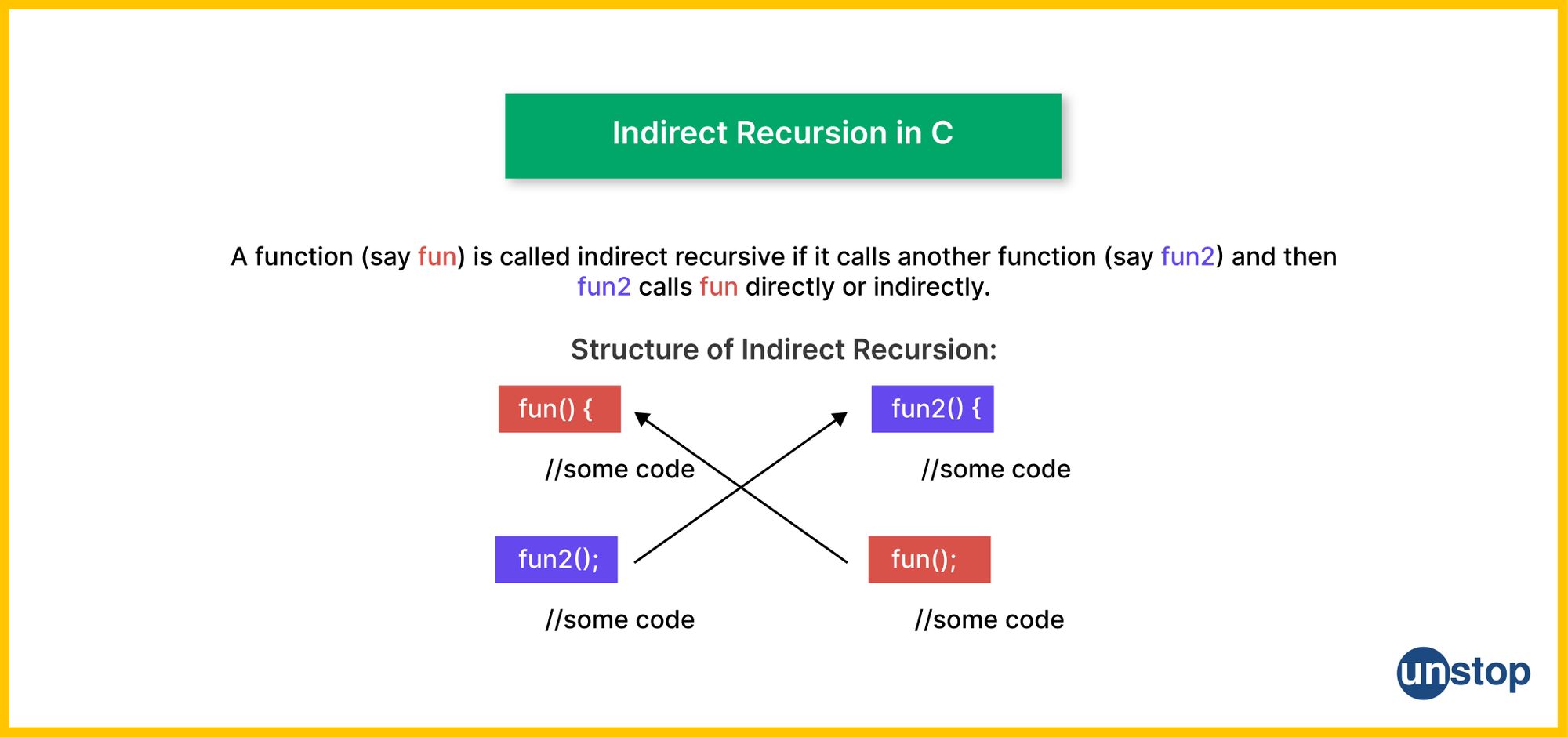
Indirect recursion occurs when two or more functions call each other in a circular manner, either directly or indirectly. In other words, the functions form a cycle of function calls, where each function calls another function in the group, eventually leading back to the original function.
Syntax:
return_type function2(parameters){
if (base_condition) { // Base case check & termination
return base_value;
}else{ // Recursive case
return function1(modified_parameters);
}
return_type function1(parameters) {
// if base case
//else recursive case calling function2()
}
Here,
- We have two recursive functions with the names function1 and function2.
- The data type of their return value and the parameters they take are given by terms return_type and parameters, respectively.
- Definition of base case and recursive case using if conditional statement remains the same.
- The difference (comparison to direct recursion) is in the recursive case/ recursive call. As seen, the recursive case for function2() calls function(), and vice versa.
Look at the C program sample below, which showcases how indirection recursion in C works.
Code Example:
#include
int function1(int n); // Forward declaration
// Indirect recursive function 2
int function2(int n) {
if (n == 0) { // Base case
return 0;
} else {
// Recursive case
return function1(n - 1);
}
}
// Indirect recursive function 1
int function1(int n) {
if (n == 0) { // Base case
return 1;
} else {
// Recursive case
return n * function2(n - 1);}
}
int main() {
// Calling the recursive functions
int result1 = function1(5);
int result2 = function2(5);
// Printing the results
printf("Result from function1: %d\n", result1);
printf("Result from function2: %d\n", result2);
return 0;
}
I2luY2x1ZGUgPHN0ZGlvLmg+CgppbnQgZnVuY3Rpb24xKGludCBuKTsgLy8gRm9yd2FyZCBkZWNsYXJhdGlvbgovLyBJbmRpcmVjdCByZWN1cnNpdmUgZnVuY3Rpb24gMgppbnQgZnVuY3Rpb24yKGludCBuKSB7CmlmIChuID09IDApIHsgLy8gQmFzZSBjYXNlCnJldHVybiAwOwp9IGVsc2UgewovLyBSZWN1cnNpdmUgY2FzZQpyZXR1cm4gZnVuY3Rpb24xKG4gLSAxKTsKfQp9CgovLyBJbmRpcmVjdCByZWN1cnNpdmUgZnVuY3Rpb24gMQppbnQgZnVuY3Rpb24xKGludCBuKSB7CmlmIChuID09IDApIHsgLy8gQmFzZSBjYXNlCnJldHVybiAxOwp9IGVsc2UgewovLyBSZWN1cnNpdmUgY2FzZQpyZXR1cm4gbiAqIGZ1bmN0aW9uMihuIC0gMSk7fQp9CgppbnQgbWFpbigpIHsKLy8gQ2FsbGluZyB0aGUgcmVjdXJzaXZlIGZ1bmN0aW9ucwppbnQgcmVzdWx0MSA9IGZ1bmN0aW9uMSg1KTsKaW50IHJlc3VsdDIgPSBmdW5jdGlvbjIoNSk7CgovLyBQcmludGluZyB0aGUgcmVzdWx0cwpwcmludGYoIlJlc3VsdCBmcm9tIGZ1bmN0aW9uMTogJWRcbiIsIHJlc3VsdDEpOwpwcmludGYoIlJlc3VsdCBmcm9tIGZ1bmN0aW9uMjogJWRcbiIsIHJlc3VsdDIpOwoKcmV0dXJuIDA7Cn0=
Output:
Result from function1: 0
Result from function2: 8
Code Explanation:
In the C code sample-
- We first forward declare function1() to inform the compiler about its existence before its actual definition.
- Then, we define a recursive function, function2(), which takes an integer parameter. In this function-
- The base case is when n is 0, where it returns 0.
- In the recursive case, it calls function1(n - 1). Here since it is calling another function, it comes indirectly recursive.
- Next, we provide the function definition for recursive function1() as follows-
- The base case is when n is 0, where it returns 1.
- In the recursive case, it multiplies n with the result of function2(n - 1). Here, function1() indirectly recursively calls function2().
- In the main() function, we call function1() and function2() with an argument of 5.
- The outcome of these function calls are stored in variables result1 and result2, respectively.
- The first call invokes function(), which recursively calls function2(), until its base case is met.
- And the second call invokes function2() which recursively calls function1(), until its base case is met.
- Finally, we use a set of printf() statements to display the results obtained from both function1() and function2() calls.
Memory Allocation Of Recursive Method In C
Understanding how memory allocation works in recursion is crucial, for programming. It involves creating activation records when calling functions, managing variables, and storing parameters. The return address is important, for controlling the flow of execution while checking for base cases determines when the recursion should stop. Developers need to grasp this process to handle memory and ensure the execution of recursive algorithms.
-
Function Call: When a recursive function is called, a new instance of the function is added to the call stack. The function parameters and local variables are allocated memory on the stack for this instance.
-
Stack Frame Creation: Each function call creates a new stack frame, also known as an activation record or stack activation, on the call stack. The stack frame contains space for:
- Function parameters
- Local variables
- Return address, i.e., the address to return to after the function completes
- Previous frame pointer, i.e., pointer to the stack frame of the calling function
-
Execution: The function executes its code, which may include additional recursive calls. Each recursive call follows the same process, creating a new stack frame and allocating memory for parameters and local variables.
-
Recursive Calls: As the recursive calls continue, the call stack grows deeper with each new function call. Each function call remains active until it reaches the base case, where the recursion stops.
-
Base Case: When the base case condition is met, the function stops making further recursive calls. At this point, the function begins to unwind the stack by returning control to the calling function.
-
Stack Unwinding: As each recursive call returns, its stack frame is deallocated, and control returns to the caller. The memory allocated for parameters and local variables in each stack frame is released.
-
Return Value Propagation: As the stack unwinds, return values from each recursive call are propagated back up the call stack to the original caller. These return values may be combined or processed as necessary, depending on the recursive algorithm.
-
Function Completion: Once the original function call completes and its return value is obtained, the memory allocated for its stack frame is also deallocated. At this point, the call stack returns to its original state before the recursive function was called.
Why Does Stack Overflow Occur In Recursion?
In general programming languages, a stack overflow occurs when the call stack, which is a region of memory used to store function calls and local variables, exceeds its predefined size.
- The call stack operates in a Last In, First Out (LIFO) manner, meaning that each function call adds a new stack frame to the top of the stack.
- When a function completes, its stack frame is removed from the top.
- If the stack grows too large due to excessive function calls or recursive calls, it can overflow, leading to a stack overflow error.
Stack Overflow & Recursion In C
As you must know, recursion involves functions calling themselves and creating a new stack frame for each recursive call. If the recursion is not properly managed, it can lead to a stack overflow. Here's how it happens:
- Excessive Recursion: When a recursive function doesn't have a proper termination condition or the termination condition is never met, it leads to an infinite loop of function calls.
- Stack Frames Accumulation: With each recursive call, a new stack frame is added to the call stack. If there is no exit condition, the stack frames keep accumulating.
- Limited Stack Space: The stack has a finite amount of space allocated to it. When the number of stack frames exceeds this limit, a stack overflow occurs.
Let's consider an example C program where we use recursion for calculation of factorial of a number and see how stack overflow occurs.
Code Example:
#include
// Recursive function for factorial calculation
int factorial(int n) {
if (n == 0) {
return 1;
} else {
return n * factorial(n - 1);
}
}
int main() {
int n = 10000; // Example input causing stack overflow
int result = factorial(n);
printf("Factorial of %d is %d\n", n, result);
return 0;
}
I2luY2x1ZGUgPHN0ZGlvLmg+CgovLyBSZWN1cnNpdmUgZnVuY3Rpb24gZm9yIGZhY3RvcmlhbCBjYWxjdWxhdGlvbgppbnQgZmFjdG9yaWFsKGludCBuKSB7CmlmIChuID09IDApIHsKcmV0dXJuIDE7Cn0gZWxzZSB7CnJldHVybiBuICogZmFjdG9yaWFsKG4gLSAxKTsKfQp9CgppbnQgbWFpbigpIHsKaW50IG4gPSAxMDAwMDsgLy8gRXhhbXBsZSBpbnB1dCBjYXVzaW5nIHN0YWNrIG92ZXJmbG93CmludCByZXN1bHQgPSBmYWN0b3JpYWwobik7CnByaW50ZigiRmFjdG9yaWFsIG9mICVkIGlzICVkXG4iLCBuLCByZXN1bHQpOwpyZXR1cm4gMDsKfQ==
Output:
Factorial of 10000 is 0
Explanation:
In the example C code, we define a recursive function called factorial() which takes an integer variable as parameter and calculates its factorial using recursive calls.
- In the main() function, we initialize an integer variable n with the value 10,000, and then call factorial() function passing n as an argument.
- When factorial(10000) is called, it recursively calls itself with decreasing values until it reaches the base case of n == 0.
- However, due to the large input value (n = 10000), the recursion depth becomes too large, causing the stack to overflow.
There are several techniques that you can use to avoid stack overflow in recursion in C. Some of the most commonly used of these are:
- Optimize the Algorithm: Analyze the recursive algorithm and see if there are any optimizations that can be made to reduce the recursion depth. Sometimes, a non-recursive approach may be more efficient.
- Use Tail Recursion: Tail recursion occurs when the recursive call is the last operation performed by the function. Some compilers optimize tail-recursive functions by reusing the same stack frame for each recursive call, thus avoiding stack overflow. However, this optimization is not guaranteed for all compilers.
- Increase Stack Size: You can increase the stack size allocated to your program, either through compiler flags or operating system settings. However, this approach may not be feasible in all environments and may only postpone the occurrence of stack overflow.
- Iterative Approach: Convert the recursive algorithm into an iterative one, if possible. Iterative algorithms typically use less stack space compared to recursive ones and are less prone to stack overflow.
Check out this amazing course to become the best version of the C programmer you can be.
Properties Of Recursion In C
It is vital to understand these characteristics of recursion in C programming language to write efficient and reliable functions. Here are some key characteristics you should know:
- Base Condition: Every recursive function needs a base condition that acts as a stopping point, preventing the function from calling itself indefinitely. Without a base condition, the function would keep calling itself, causing a stack overflow.
- Recursive Case: The recursive case is where the function calls itself to solve a version of the problem at hand. This is the essence of recursion—breaking down a complex problem into simpler sub-problems. Each recursive call should move closer to reaching the base condition for termination to occur.
- Termination Statement: When the base condition is met, a termination statement is executed. This statement defines what value or action will halt the recursion and contribute to producing the result.
- Memory Usage: Recursion in C programming uses the call stack to manage function calls. Each recursive call adds a new frame to the stack. Understanding the memory implications is essential to avoid stack overflow errors.
- Efficiency and Performance: While recursive solutions may seem elegant and intuitive, they might not always be the best option as recursive function calls can add some overhead. That is, iterative solutions can offer better performance, especially for straightforward linear processes. Considering the nature of the problem and efficiency are hence vital when choosing between iteration and recursion in C.
- Clarity and Readability: One of the advantages of recursion in C is its ability to express algorithms naturally. Recursive code often mirrors the problem statement, making it clearer and easier to understand.
- Divide and Conquer: Recursion in C inherently follows the divide and conquer approach. It allows us to break down problems into more manageable subproblems. This property is useful when search, sort, and traversal problems/ tasks.
- Elegance in Solutions: Recursion can lead to concise solutions for specific problems, i.e., those that naturally lend themselves to being divided into subproblems. In such cases, recursion in C often has solutions that are also more expressive compared to their iterative counterparts.
- Potential for Stack Overflow: Recursive functions can lead to a stack overflow if not managed properly, i.e., when the call stack exhausts its available space due to excessive recursive calls. Understanding the depth of recursion and optimizing the code (such as using tail recursion) can help mitigate this risk.
Examples Of Recursion In C
By now, you must have a grasp of the concept of recursion in C programming. In this section, we will look at a few common examples to illustrate how to write and run C programs that make correct use of recursion code to solve problems, i.e., how to implement recursion in C programs.
C Program To Show Infinite Recursive Function In C (Eg- Fibonacci Series)
The Fibonacci series is one where every term is the sum of two previous consecutive terms. It features in a lot of programming and computational concepts. We can write a code to generate this series with the help of recursion in C.
- That is, we can define a recursive function, say, Fibonacci function that uses recursive function calls (linear recursion) to efficiently calculate series and the nth term in the Fibonacci sequence.
- The time complexity of this recursive Fibonacci approach is exponential, making it less efficient for large values of n. Memoization or an iterative approach can improve performance.
Code Example:
#include
// Recursive function to calculate the nth term in the Fibonacci sequence
int fibonacci(int n) {
// Base condition
if (n == 0)
return 0;
else if (n == 1)
return 1;
// Recursive case
else
return fibonacci(n - 1) + fibonacci(n - 2);
}
// Function to print the Fibonacci sequence up to the nth term
void printFibonacciSequence(int n) {
printf("Fibonacci Sequence up to the %dth term: ", n);
for (int i = 0; i <= n; ++i) {
printf("%d ", fibonacci(i));
}
printf("\n");
}
int main() {
int term;
// Take user input for term
printf("Enter the position in the Fibonacci sequence: ");
scanf("%d", &term);
// Check if the entered value is non-negative
if (term < 0) {
printf("Please enter a non-negative integer.\n");
return 1; // Exit with an error code
}
int result = fibonacci(term);
printf("The %dth term in the Fibonacci sequence is: %d\n", term, result);
printFibonacciSequence(term); // Print the Fibonacci sequence up to the nth term
return 0;
}
I2luY2x1ZGUgPHN0ZGlvLmg+CgovLyBSZWN1cnNpdmUgZnVuY3Rpb24gdG8gY2FsY3VsYXRlIHRoZSBudGggdGVybSBpbiB0aGUgRmlib25hY2NpIHNlcXVlbmNlCmludCBmaWJvbmFjY2koaW50IG4pIHsKLy8gQmFzZSBjb25kaXRpb24KaWYgKG4gPT0gMCkKcmV0dXJuIDA7CmVsc2UgaWYgKG4gPT0gMSkKcmV0dXJuIDE7Ci8vIFJlY3Vyc2l2ZSBjYXNlCmVsc2UKcmV0dXJuIGZpYm9uYWNjaShuIC0gMSkgKyBmaWJvbmFjY2kobiAtIDIpOwp9CgovLyBGdW5jdGlvbiB0byBwcmludCB0aGUgRmlib25hY2NpIHNlcXVlbmNlIHVwIHRvIHRoZSBudGggdGVybQp2b2lkIHByaW50Rmlib25hY2NpU2VxdWVuY2UoaW50IG4pIHsKcHJpbnRmKCJGaWJvbmFjY2kgU2VxdWVuY2UgdXAgdG8gdGhlICVkdGggdGVybTogIiwgbik7CmZvciAoaW50IGkgPSAwOyBpIDw9IG47ICsraSkgewpwcmludGYoIiVkICIsIGZpYm9uYWNjaShpKSk7Cn0KcHJpbnRmKCJcbiIpOwp9CgppbnQgbWFpbigpIHsKCmludCB0ZXJtOwovLyBUYWtlIHVzZXIgaW5wdXQgZm9yIHRlcm0KcHJpbnRmKCJFbnRlciB0aGUgcG9zaXRpb24gaW4gdGhlIEZpYm9uYWNjaSBzZXF1ZW5jZTogIik7CnNjYW5mKCIlZCIsICZ0ZXJtKTsKCi8vIENoZWNrIGlmIHRoZSBlbnRlcmVkIHZhbHVlIGlzIG5vbi1uZWdhdGl2ZQppZiAodGVybSA8IDApIHsKcHJpbnRmKCJQbGVhc2UgZW50ZXIgYSBub24tbmVnYXRpdmUgaW50ZWdlci5cbiIpOwpyZXR1cm4gMTsgLy8gRXhpdCB3aXRoIGFuIGVycm9yIGNvZGUKfQoKaW50IHJlc3VsdCA9IGZpYm9uYWNjaSh0ZXJtKTsKcHJpbnRmKCJUaGUgJWR0aCB0ZXJtIGluIHRoZSBGaWJvbmFjY2kgc2VxdWVuY2UgaXM6ICVkXG4iLCB0ZXJtLCByZXN1bHQpOwpwcmludEZpYm9uYWNjaVNlcXVlbmNlKHRlcm0pOyAvLyBQcmludCB0aGUgRmlib25hY2NpIHNlcXVlbmNlIHVwIHRvIHRoZSBudGggdGVybQoKcmV0dXJuIDA7Cn0=
Output:
Enter the position in the Fibonacci sequence: 5
The 5th term in the Fibonacci sequence is: 5
Fibonacci Sequence up to the 5th term: 0 1 1 2 3 5
For more read: Fibonacci Series Using Recursion In C (With Detailed Explanation)
Find The Factorial Of A Number Using Recursion In C
The factorial of a number refers to the product of all consecutive positive numbers before the respective number (itself included). As is obvious, we can use linear recursion for calculation of factorial of a number in programming. The general approach here would be-
- Define a recursive function, say Factorial function, with a base case to handle the factorial of 0 and 1.
- For n greater than 1, the function should use recursive case/ recursion to calculate the factorial by multiplying n with the factorial of (n-1).
Look at the C program example below which showcases how this is implemented in action.
Code Example:
#include
// Recursive function to calculate factorial
int factorial(int n) {
// Base condition
if (n == 0 || n == 1) {
return 1; // Factorial of 0 and 1 is 1
}else { // Recursive call
return n * factorial(n - 1);}
}
int main() {
int num;
// Take user input for num
printf("Enter a number: ");
scanf("%d", &num);
int result = factorial(num);
printf("Factorial of %d is %d\n", num, result);
return 0;
}
I2luY2x1ZGUgPHN0ZGlvLmg+CgovLyBSZWN1cnNpdmUgZnVuY3Rpb24gdG8gY2FsY3VsYXRlIGZhY3RvcmlhbAppbnQgZmFjdG9yaWFsKGludCBuKSB7Ci8vIEJhc2UgY29uZGl0aW9uCmlmIChuID09IDAgfHwgbiA9PSAxKSB7CnJldHVybiAxOyAvLyBGYWN0b3JpYWwgb2YgMCBhbmQgMSBpcyAxCn1lbHNlIHsgLy8gUmVjdXJzaXZlIGNhbGwKcmV0dXJuIG4gKiBmYWN0b3JpYWwobiAtIDEpO30KfQoKaW50IG1haW4oKSB7CgppbnQgbnVtOwovLyBUYWtlIHVzZXIgaW5wdXQgZm9yIG51bQpwcmludGYoIkVudGVyIGEgbnVtYmVyOiAiKTsKc2NhbmYoIiVkIiwgJm51bSk7CgppbnQgcmVzdWx0ID0gZmFjdG9yaWFsKG51bSk7CnByaW50ZigiRmFjdG9yaWFsIG9mICVkIGlzICVkXG4iLCBudW0sIHJlc3VsdCk7CgpyZXR1cm4gMDsKfQ==
Output:
Enter a number: 5
Factorial of 5 is 120
For more info, read: C Program To Find Factorial Of A Number (Multiple Ways + Examples)
Calculating The Sum of Natural Numbers Using Recursion In C
Another common operation that features in programming, computation and other fields is calculating the sum of N natural or N numbers. There are multiple ways to complete this task, such as iterative code/ approach using loops, mathematical formulas and even recursion.
Yes, we can solve this problem using recursion in C. For this-
- You can define a recursive function that recursively adds the current number (n) to the sum of natural numbers up to (n-1).
- The base case must ensure the recursion stops when n reaches 1.
- The recursive case must keep adding the sum in the previous recursive call to the current parameter value.
Code Example:
#include
// Recursive function to calculate the sum of natural numbers
int sumOfNaturalNumbers(int n) {
// Base case
if (n == 1) {
return 1;
}else { // Recursive case
return n + sumOfNaturalNumbers(n - 1);}
}
int main() {
int n = 3;
int result = sumOfNaturalNumbers(n);
printf("Sum of Natural Numbers up to %d: %d\n", n, result);
return 0;
}
I2luY2x1ZGUgPHN0ZGlvLmg+CgovLyBSZWN1cnNpdmUgZnVuY3Rpb24gdG8gY2FsY3VsYXRlIHRoZSBzdW0gb2YgbmF0dXJhbCBudW1iZXJzCmludCBzdW1PZk5hdHVyYWxOdW1iZXJzKGludCBuKSB7Ci8vIEJhc2UgY2FzZQppZiAobiA9PSAxKSB7CnJldHVybiAxOwp9ZWxzZSB7IC8vIFJlY3Vyc2l2ZSBjYXNlCnJldHVybiBuICsgc3VtT2ZOYXR1cmFsTnVtYmVycyhuIC0gMSk7fQp9CgppbnQgbWFpbigpIHsKCmludCBuID0gMzsKaW50IHJlc3VsdCA9IHN1bU9mTmF0dXJhbE51bWJlcnMobik7CnByaW50ZigiU3VtIG9mIE5hdHVyYWwgTnVtYmVycyB1cCB0byAlZDogJWRcbiIsIG4sIHJlc3VsdCk7CgpyZXR1cm4gMDsKfQ==
Output:
Sum of Natural Numbers up to 3: 6
The code comments indicate how we define the function to use recursion in C. You can also read the following for more: How To Find Sum Of N Natural Numbers In C? (8 Methods + Codes)
Advantages & Disadvantages Of Recursion In C
Recursion in C offers several advantages and disadvantages, which are important to consider when deciding whether to use recursive approaches in programming.
Advantages Of Recursion In C
- Elegant Solutions: Recursive solutions can often provide elegant and concise solutions to problems, especially those that can be naturally expressed in terms of smaller subproblems.
- Readability: The definition of function using recursion in C can mirror the mathematical definition of a problem. This makes the code easier to understand and maintain, particularly for problems that are recursive in nature.
- Divide and Conquer: Recursive algorithms often follow the 'divide and conquer' approach, i.e., they break down a problem into smaller, more manageable subproblems. This can lead to efficient solutions for certain types of problems.
- Modularity: Definition of function using recursion in C programs, can make code more modular. That is, the function signature can be designed to solve a single, specific task, making the code more modular and reusable.
- Dynamic Memory Allocation: Recursion in C can be useful for problems involving dynamic memory allocation, such as tree traversal or graph traversal, where the number of recursive calls corresponds to the dynamic structure of the problem.
Disadvantages Of Recursion In C
- Performance Overhead: Recursive functions often come with a performance overhead due to the additional function calls and stack management. This can lead to slower execution times and increased memory usage, especially for deep recursion.
- Stack Overflow: If not implemented carefully, recursion in C programs can lead to stack overflow errors. This is particularly true when dealing with large input sizes or deep recursion levels as the call stack grows too large due to excessive recursive calls.
- Difficulty in Debugging: Recursive functions can be more challenging to debug compared to iterative solutions (and non-recursive functions). This is because recursive functions involve multiple function calls and stack frames. All in all, the program control/ flow of execution and identifying errors can be more complex when using recrusion in C.
- Limited Tail Recursion Optimization: While some compilers optimize tail-recursive functions to reduce stack space, not all compilers support this optimization. This limitation can impact the efficiency of certain algorithms for recursion in C.
- Space Complexity: Recursive solutions may consume more memory compared to iterative solutions, as each recursive call adds a new stack frame to the call stack. This can be a concern for memory-constrained environments or when dealing with large input sizes.
While recursion in C is a powerful tool for solving complex tasks/ problems, it's important to weigh its advantages against its potential drawbacks. That is, you must consider factors such as performance, memory usage, and ease of debugging when deciding whether to use recursion in C programs.
Difference Between Iteration & Recursion In C
Iteration and recursion both centre around the concept of repeating a certain step/ process over and over again until a solution is reached or tasks are fulfilled. This similarity in their nature makes it difficult for many to differentiate between the fundamentally different problem-solving methods. That is-
- Iteration involves use of loop control statements for repetitive execution of code, with a fixed set of instructions repeated until a specified condition is met.
- While, recursion employs a self-referential function calling mechanism, breaking down a problem into simpler instances until a base case is reached.
Knowing the difference is essential to choosing the right programming strategy for your needs. The table below highlights the key differences between iteration and recursion in C programming.
| Basis | Iteration | Recursion |
| Definition | Repeated execution of a set of instructions using looping statements. | A process in which a function calls itself directly or indirectly. |
| Control Structure | Determined by the respective type of loop, i.e., for loop, while loop, do-while loop. | Structured like a function but contains conditional statements to manage recursion. |
| Termination | Terminates when the loop condition is false. | Terminates when a base case is met. |
| Code Structure | Typically involves a block of code with explicit looping constructs. | Often involves a function with base case checks. |
| Memory Usage | Generally uses less memory as it doesn't involve function calls and stack frames. | May use more memory due to function call overhead and the call stack. |
| Readability | May become complex for certain algorithms, particularly if nested loops are involved. | Often results in cleaner and more intuitive code, especially for certain algorithms. |
| Performance | Can be more performant for certain simple and straightforward tasks. | May have higher time and space complexity for certain problems, especially if not optimized. |
| Examples | for (int i = 0; i < 5; ++i) { /* code */ } |
void recursiveFunction(int n) { if (n > 0) { recursiveFunction(n - 1); } } |
| Use Cases | Well-suited for tasks with clear iterations and simple logic. | Preferred for tasks with recursive structures, tree traversals, and divide-and-conquer problems. |
| Debugging | Generally easier to debug due to straightforward flow. | It can be more challenging to debug, especially with deep recursion and complex base cases. |
| Tail Recursion | It is not applicable as iteration doesn't involve recursion. | It can be optimized by some compilers to reduce stack overhead, making it similar to iteration in efficiency. |
Difference Between Direct & Indirect Recursion In C
The main distinction between direct and indirect recursion in C lies in how the recursive calls happen/ functions call each other. That is, the caller function, base function/ calling function, etc., differ, leading to the distinction.
- Direct recursion occurs when a function directly calls itself, leading to a repetitive cycle until a base case is met.
- Indirect recursion, on the other hand, involves a sequence of functions circularly calling one another, ultimately forming a loop.
It is essential to understand these distinctions to deign affective recursive algorithm and improve code structure. The table below highlights the differences between the two types of recursion in C.
|
Basis |
Direct Recursion |
Indirect Recursion |
|
Definition |
A function calls itself directly. |
Function A calls function B, and function B calls function A, creating a cycle. |
|
Function Calls |
Directly calls itself within its own definition |
Involves a chain of function calls, possibly including other functions in between |
|
Base Case |
It has only one base case, which is essential to prevent infinite recursion. |
Every function must have a base case to prevent infinite recursion. |
|
Code Structure |
Often simpler and more straightforward. |
It may involve multiple functions and can be more complex. |
|
Memory Usage |
Generally, less memory overhead as there's a single function's call stack. |
It may have higher memory usage due to multiple functions' call stacks. |
|
Control Flow |
The control flow is more direct and linear. |
Control flow may be less intuitive due to the chain of function calls. |
|
Example/ Use Case |
Calculating factorials, Fibonacci, and simple recursive structures. |
Complex problems where two or more functions need to call each other. |
|
Code Readability |
Often more readable for simple recursive patterns. |
May be less readable due to the interdependence of multiple functions |
|
Tail Recursion Optimization |
Tail recursion optimization is more feasible. |
Tail recursion optimization may be less effective, depending on the compiler. |
|
Debugging Complexity |
Generally easier to debug due to a simpler structure. |
It may be more challenging to debug, especially with a large number of functions involved. |
Looking for mentors? Find the perfect mentor for select experienced coding & software experts here.
Conclusion
Recursion in C and programming in general helps solve complex problems (or fulfill complex tasks) by splitting it down into smaller sub-problems/ tasks. The premise of recursive approach is to divide a problem into smaller instances and then repeatedly apply a single procedure solve each sub-problem, and effectively the larger problem.
The components for implementation of recursion in C, include the base case, recursive case, and recursive call/ action. While recursion provides several advantages, such as simplicity, reduction of complexity, and efficiency in certain cases. It is essential to use recursion judiciously as excessive use might lead to infinite recursion and stack overflow errors. Additionally, iterative solutions may be preferred when recursion in C introduces unnecessary overhead or memory consumption.
Also read: 100+ Top C Interview Questions With Answers (2024)
Frequently Asked Questions
Q. List some important points to remember while using recursion in C.
When using recursion in C, it is important to keep several key points in mind to ensure correct and efficient execution:
- Base Case: Always define a clear and correct base case to prevent infinite recursion and potential stack overflow. The base case is the condition that, when true, stops the recursive function from calling itself.
- Stack Usage: Be aware that each recursive call consumes stack space. Deep recursion in C programs can lead to stack overflow, so ensure that your recursion depth is manageable.
- Termination Condition: Ensure that each recursive call progresses towards the base case. This means the problem size should reduce with each recursive call, eventually leading to the base case.
- Performance: Recursive functions can be less efficient than their iterative counterparts due to function calls and stack management overhead. If possible, optimize the algorithm for recursion in C, or consider an iterative approach if performance is critical.
- Tail Recursion: If applicable, use tail recursion in C, where the recursive call is the last operation in the function. Compilers can optimize tail-recursive functions to reduce the stack space used, similar to iteration.
Q. What is the difference between a base case and a recursive case?
The recursive and base case are essential components for implementing recursion in C programming. The table below lists the important differences between the two.
|
Basis |
Base Case |
Recursive Case |
|
Definition |
A condition that, when met, stops the recursion. |
A set of instructions or function calls that contributes to the recurrence of the function. |
|
Role |
Determines when the recursion should stop. |
Defines the behaviour of the function for inputs other than those covered by the base case. |
|
Execution |
Typically, it results in a straightforward computation or simple action. |
Often involves calling the function itself with modified parameters. |
|
Termination |
Causes the recursion to terminate. |
Continues the recursion or contributes to the progression toward the base case |
|
Occurrence |
Usually appears at the beginning or early stages of the recursive function. |
Appears after the base case check and contributes to the repetition of the function. |
Q. Why do we prefer iteration over recursion in any C program?
Iteration is often or might be preferred over recursion in C programs primarily due to performance and memory efficiency.
- Iterative solutions typically use loops that have a constant memory footprint regardless of the number of iterations.
- In contrast, recursive solutions involve multiple function calls, each consuming stack space, which can lead to stack overflow for deep recursion levels.
- Additionally, function calls in recursion add overhead due to the need to maintain multiple stack frames, which can slow down execution.
- Iterative solutions also tend to be more straightforward to debug and understand, as they avoid the complexity of managing multiple recursive calls.
Thus, for problems where both iterative and recursive approaches are feasible, iteration is generally more efficient and practical in C programming.
Q. What is the difference between tailed and non-tailed recursion in C?
|
Basis |
Tailed Recursion |
Non-Tailed (Non-Tail) Recursion |
|
Definition |
A form of recursion where the recursive call is the last operation in the function. |
A form of recursion where the recursive call is not the last operation in the function. |
|
Tail Call Optimization |
Well-suited for Tail Call Optimization (TCO) by certain compilers. |
Less amenable to Tail Call Optimization. |
|
Memory Usage |
Tends to have more efficient memory usage due to potential optimization. |
This may result in additional stack frames, potentially leading to higher memory usage. |
|
Performance |
It can potentially be more performant due to TCO optimization. |
It may have slightly lower performance, especially for deep recursion. |
|
Example (Tail Recursive) |
int tailSum(int n, int accumulator) { |
int nonTailSum(int n){ |
|
Optimization Possibility |
More likely to benefit from TCO optimization. |
Less likely to benefit from TCO optimization. |
Q. What are the applications of recursion?
Recursion stands as a potent technique with diverse applications. Several common applications recursion in C programming are:
- Tree and Graph Traversal: Recursion plays a pivotal role in systematically traversing and searching data structures like trees and graphs. Recursive algorithms effectively explore all nodes or vertices within a tree or graph.
- Sorting Algorithms: Recursive algorithms find utility in sorting procedures, such as quicksort and merge sort. These algorithms leverage recursion to partition data into smaller subarrays or sublists, sorting them individually before merging them back together.
- Divide-and-Conquer Algorithms: Numerous algorithms adopting a divide-and-conquer approach, including the binary search algorithm, employ recursion to break down complex problems into more manageable subproblems.
- Fractal Generation: The creation of intricate fractal shapes and patterns is made possible through recursive algorithms. For instance, the Mandelbrot set is crafted by iteratively applying a recursive formula to complex numbers.
- Backtracking Algorithms: Tackling problems involving a sequence of decisions, where each choice hinges on prior ones, is a domain where backtracking algorithms excel. Recursion is instrumental in implementing these algorithms to systematically explore all potential paths and backtrack when a solution remains elusive.
- Memorization: A strategic approach known as memorization involves storing results from resource-intensive function calls and retrieving cached outcomes when identical inputs reappear. Recursive functions are instrumental in implementing memoization to compute and cache results for subproblems.
Q. Can a recursive function have multiple base cases? (Example)
Yes, we can have multiple base cases in a recursive function. In fact, it is common practice in situations where problems may have multiple termination conditions.
- Here, each base case represents a condition in which the recursive function stops generating recursive calls and instead directly produces a result.
- By incorporating mulitple base cases, the recursive function becomes equipped to tackle situations or input values in a customized manner.
- Multiple base cases are also essential when addressing problems requiring specialized handling for different input scenarios.
- Note that each unique base case enables the function to offer tailored responses to situations, thereby enhancing the algorithm's flexibility and overall functionality.
Below is a C program example, which shows an implementation of recursion in C with multiple base cases.
Code Example:
#include
// Recursive function with multiple base cases
int recursiveFunction(int n) {
if (n == 0) { // Base case 1: If n is zero, return 0
return 0;}
if (n < 0) { // Base case 2: If n is negative, return a predefined value
return -1;}
// Recursive case: Call the function with modified parameters
return n + recursiveFunction(n - 1);
}
int main() {
int result1 = recursiveFunction(5); // Positive input
int result2 = recursiveFunction(0); // Zero input
int result3 = recursiveFunction(-3); // Negative input
// Displaying the results
printf("Result 1: %d\n", result1);
printf("Result 2: %d\n", result2);
printf("Result 3: %d\n", result3);
return 0;
}
I2luY2x1ZGUgPHN0ZGlvLmg+CgovLyBSZWN1cnNpdmUgZnVuY3Rpb24gd2l0aCBtdWx0aXBsZSBiYXNlIGNhc2VzCmludCByZWN1cnNpdmVGdW5jdGlvbihpbnQgbikgewppZiAobiA9PSAwKSB7IC8vIEJhc2UgY2FzZSAxOiBJZiBuIGlzIHplcm8sIHJldHVybiAwCnJldHVybiAwO30KaWYgKG4gPCAwKSB7IC8vIEJhc2UgY2FzZSAyOiBJZiBuIGlzIG5lZ2F0aXZlLCByZXR1cm4gYSBwcmVkZWZpbmVkIHZhbHVlCnJldHVybiAtMTt9Ci8vIFJlY3Vyc2l2ZSBjYXNlOiBDYWxsIHRoZSBmdW5jdGlvbiB3aXRoIG1vZGlmaWVkIHBhcmFtZXRlcnMKcmV0dXJuIG4gKyByZWN1cnNpdmVGdW5jdGlvbihuIC0gMSk7Cn0KCmludCBtYWluKCkgewoKaW50IHJlc3VsdDEgPSByZWN1cnNpdmVGdW5jdGlvbig1KTsgLy8gUG9zaXRpdmUgaW5wdXQKaW50IHJlc3VsdDIgPSByZWN1cnNpdmVGdW5jdGlvbigwKTsgLy8gWmVybyBpbnB1dAppbnQgcmVzdWx0MyA9IHJlY3Vyc2l2ZUZ1bmN0aW9uKC0zKTsgLy8gTmVnYXRpdmUgaW5wdXQKCi8vIERpc3BsYXlpbmcgdGhlIHJlc3VsdHMKcHJpbnRmKCJSZXN1bHQgMTogJWRcbiIsIHJlc3VsdDEpOwpwcmludGYoIlJlc3VsdCAyOiAlZFxuIiwgcmVzdWx0Mik7CnByaW50ZigiUmVzdWx0IDM6ICVkXG4iLCByZXN1bHQzKTsKCnJldHVybiAwOwp9
Output:
Result 1: 15
Result 2: 0
Result 3: -1
Explanation:
In the C code example-
- We define a function called recursiveFunction(), which takes an integer parameter n and computes the sum of positive integers up to n.
- As seen in the function definition, we have two if-statements to define base cases.
- The first base case stipulates that if the parameter n equals 0, then the function should return 0 and terminate.
- The second base case stipulates that if the parameter value is negative, then the function should return -1 and terminate.
- In the main(0 function, we showcase three scenarios, i.e., positive input (5), zero input (0), and negative input (-3), each yielding a distinct result.
- The function employs two base cases to terminate recursion in C code when n reaches either zero or becomes negative.
Here are a few other topics you must explore:
- Structure In C | Create, Access, Modify & More (+Code Examples)
- Union In C | Declare, Initialize, Access Member & More (Examples)
- Arrays In C | Declare, Initialize, Manipulate & More (+Code Examples)
- Type Casting In C | Cast Functions, Types & More (+Code Examples)
- Bitwise Operators In C Programming Explained With Code Examples
An economics graduate with a passion for storytelling, I thrive on crafting content that blends creativity with technical insight. At Unstop, I create in-depth, SEO-driven content that simplifies complex tech topics and covers a wide array of subjects, all designed to inform, engage, and inspire our readers. My goal is to empower others to truly #BeUnstoppable through content that resonates. When I’m not writing, you’ll find me immersed in art, food, or lost in a good book—constantly drawing inspiration from the world around me.
Login to continue reading
And access exclusive content, personalized recommendations, and career-boosting opportunities.
Subscribe
to our newsletter












Comments
Add comment